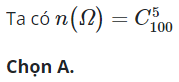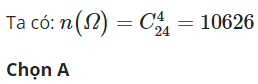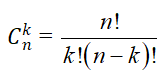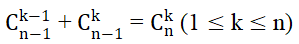Trắc nghiệm Toán 11 Bài 4: Phép thử và biến cố
-
738 lượt thi
-
17 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:
Xem đáp án
Chọn D.
Phép thử ngẫu nhiên là phép thử mà ta chưa biết được kết quả là gì.
Đáp án D không phải là phép thử vì ta biết chắc chắn kết quả chỉ có thể là một số cụ thể số bi xanh và số bi đỏ.
Câu 2:
21/07/2024Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là:
Xem đáp án
Chọn C.
Liệt kê các phần tử.
Câu 3:
16/07/2024Cho phép thử có không gian mẫu . Các cặp biến cố không đối nhau là:
Xem đáp án
Chọn C.
Cặp biến cố không đối nhau là 
và 
Câu 4:
23/07/2024Một hộp đựng 10 thẻ, đánh số từ 1 đến 10. Chọn ngẫu nhiên thẻ. Gọi A là biến cố để tổng số của 3 thẻ được chọn không vượt quá 8. Số phần tử của biến cố là:
Xem đáp án
Chọn C.
Liệt kê ta có:
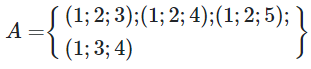
Câu 5:
22/07/2024Xét phép thử tung con súc sắc 6 mặt hai lần. Xác định số phần tử của không gian mẫu
Xem đáp án
Chọn A.
Không gian mẫu gồm các bộ
i nhận 6 giá trị, j cũng nhận 6 giá trị nên có
Vậy 
Câu 8:
23/07/2024Một xạ thủ bắn liên tục 4 phát đạn vào bia. Gọi
A: “Lần thứ tư mới bắn trúng bia’’
Xem đáp án
Ta có:
bắn không trúng bia.
Câu 9:
16/07/2024Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của biến cố: A: “ 4 viên bi lấy ra có đúng hai viên bi màu trắng”:
Xem đáp án
Số cách chọn 4 viên bi có đúng hai viên bị màu trắng là:
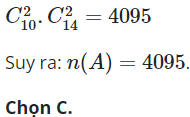
Câu 10:
20/07/2024Gieo một đồng tiền và một con súcsắc. Số phần tử của không gian mẫu là:
Xem đáp án
Chọn B.
Câu 11:
25/11/2024Có 100 tấm thẻ được đánh số từ 1 đến 100. Lấy ngẫu nhiên 5 thẻ. Tính số phần tử của biến cố B: “ Có ít nhất một số ghi trên thẻ được chọn chia hết cho 3”.
Xem đáp án
Đáp án đúng là D.
Lời giải
Từ 1 đến 100 có 33 số chia hết cho 3. Do đó, số cách chọn 5 tấm thẻ mà không có tấm thẻ nào ghi số chia hết cho 3 là:
*Phương pháp giải:
Dùng phương pháp biến cố đối:
- Xác định số cách chọn mà cả lần đều không có tấm thẻ nào chia hết cho
- Số phần tử của là
*Lý thuyết:
a) Định nghĩa:
- Giả sử A có n phần tử (n ≥ 1). Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).
- Quy ước: Tổ hợp chập 0 của n phần tử là tập rỗng.
b) Số các tổ hợp:
- Kí hiệu Cnk là số các tổ hợp chập k của n phần tử (0 ≤ k ≤ n).
- Định lý:
c) Tính chất của các số Cnk
- Tính chất 1:
Cnk = Cnn - k (0 ≤ k ≤ n)
- Tính chất 2:
Xem thêm
Lý thuyết Tổ hợp - xác suất hay, chi tiết
Câu 14:
23/11/2024Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện đúng 1 lần là:
Xem đáp án
Đáp án đúng là A
Lời giải
*Phương pháp giải:
Khi gieo đồng tiền có hai khả năng là sắp hoặc ngửa
*Lý thuyết:
a) Định nghĩa
Nhận xét:
- Mỗi sự kiện liên quan đến phép thử T tương ứng với một (và chỉ một) tập con A của không gian mẫu Ω.
- Ngược lại, mỗi tập con A của không gian mẫu Ω có thể phát biểu dưới dạng mệnh đề nêu sự kiện liên quan đến phép thử T.
Định nghĩa:
Biến cố ngẫu nhiên (gọi tắt là biến cố) là một tập con của không gian mẫu.
Chú ý: Vì sự kiện chỉ ra tính chất đặc trưng cho các phần tử của một biến cố nên ta cũng gọi sự kiện là biến cố. Chẳng hạn “Kết quả của hai lần tung là giống nhau” trong phép thử “Tung một đồng xu hai lần liên tiếp” là một biến cố.
b) Biến cố không. Biến cố chắc chắn
Xét phép thử T với không gian mẫu Ω. Mỗi biến cố là một tập con của tập Ω. Vì thế, tập hợp ∅ cũng là một biến cố, gọi là biến cố không thể (gọi tắt là biến cố không). Còn tập hợp Ω gọi là biến cố chắc chắn.
Xem thêm
Xác suất của biến cố | Lý thuyết, công thức, các dạng bài tập và cách giải
Câu 15:
23/11/2024Gieo ngẫu nhiên 2 đồng tiền thì không gian mẫu của phép thử có bao nhiêu biến cố:
Xem đáp án
Đáp án đúng là A.
Lời giải
Mô tả không gian mẫu ta có: 
*Phương pháp giải:
Số phần tử của không gian mẫu là 4 vì mỗi đồng xu có 2 khả năng có thể xảy ra
*Lý thuyết:
1. Phép thử ngẫu nhiên và không gian mẫu
– Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó.
– Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu, kí hiệu là Ω.
– Chú ý: Trong chương này ta chỉ xét các phép thử mà không gian mẫu gồm hữu hạn phần tử.
Ví dụ: Xúc xắc có 6 mặt đánh số chấm từ 1 chấm đến 6 chấm. Không gian mẫu của 1 lần tung xúc xắc là Ω = {1; 2; 3; 4; 5; 6}.
Phép thử: Tung xúc xắc 2 lần sẽ có không gian mẫu gồm 6.6 = 36 cách xuất hiện mặt của xúc xắc.
2. Biến cố
– Mỗi tập con của không gian mẫu được gọi là một biến cố, kí hiệu là A, B, C, …
– Một kết quả thuộc A được gọi là kết quả làm cho A xảy ra, hoặc kết quả thuận lợi cho A.
– Biến cố chắc chắn là biến cố luôn xảy ra, kí hiệu là Ω.
– Biến cố không thể là biến cố không bao giờ xảy ra, kí hiệu là ∅.
– Đôi khi ta cần dùng các quy tắc đếm và công thức tổ hợp để xác định số phần tử của không gian mẫu và số kết quả thuận lợi cho mỗi biến cố.
Xem thêm
Lý thuyết Không gian mẫu và biến cố – Toán 10 Chân trời sáng tạo
Câu 16:
25/11/2024Có 100 tấm thẻ được đánh số từ 1 đến 100. Lấy ngẫu nhiên 5 thẻ. Tính số phần tử của biến cố A: “ Số ghi trên các tấm thẻ được chọn là số chẵn”
Xem đáp án
Đáp án đúng là C.
Lời giải
Trong 100 tấm thẻ có 50 tấm được ghi các số chẵn, do đó
*Phương pháp giải:
Sử dụng công thức tổ hợp để tính phần tử A
*Lý thuyết:
a) Định nghĩa:
- Giả sử A có n phần tử (n ≥ 1). Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).
- Quy ước: Tổ hợp chập 0 của n phần tử là tập rỗng.
b) Số các tổ hợp:
- Kí hiệu Cnk là số các tổ hợp chập k của n phần tử (0 ≤ k ≤ n).
- Định lý:
c) Tính chất của các số Cnk
- Tính chất 1:
Cnk = Cnn - k (0 ≤ k ≤ n)
- Tính chất 2:
Xem thêm
Lý thuyết Tổ hợp - xác suất hay, chi tiết
Câu 17:
06/11/2024Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của biến cố: C: “ 4 viên bi lấy ra có đủ 3 màu”
Xem đáp án
Đáp án đúng là C
Lời giải
Số cách lấy 4 viên bi chỉ có một màu là:
*Phương pháp giải:
Bước 1: Xác định biến cố của các xác suất, có thể gọi tên các biến cố A; B; C; D để biểu diễn.
Bước 2: Tìm mối quan hệ giữa các biến cố vừa đặt tên, biểu diễn biến cố trung gian và quan trọng nhất là biến cố đề bài đang yêu cầu tính xác suất thông qua các biến cố ở bước 1.
Bước 3: Sử dụng các mối quan hệ vừa xác định ở bước 2 để chọn công thức cộng hay công thức nhân phù hợp.
*Lý thuyết:
a) Công thức cộng xác suất
- Nếu thì A và B được gọi là hai biến cố xung khắc.
- Nếu hai biến cố A, B xung khắc nhau thì
- Nếu các biến cố A1 ; A2; A3 ; … An đôi một xung khắc với nhau thì
- Công thức tính xác suất của biến cố đối:
- Mở rộng: Với hai biến cố bất kì cùng liên quan đến phép thử thì:
b) Công thức nhân xác suất
- Hai biến cố gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra biến cố kia.
- Nếu A và B là hai biến cố độc lập khi và chỉ khi
- Một cách tổng quát, nếu k biến cố A1,A2,A3,...,Ak là độc lập thì
* Chú ý:
Nếu A và B độc lập thì A và độc lập, B và độc lập, và độc lập. Do đó nếu A và B độc lập thì ta còn có các đẳng thức
Xem thêm
Lý thuyết Xác suất của biến cố (mới + Bài Tập) – Toán 11