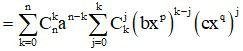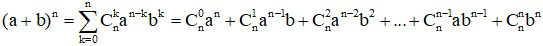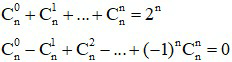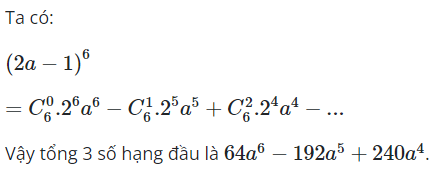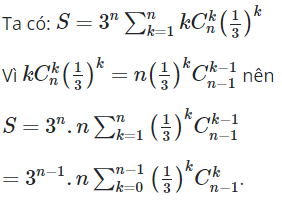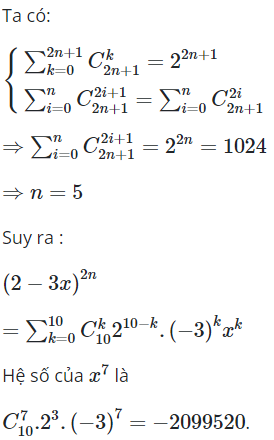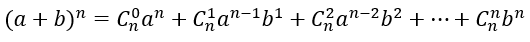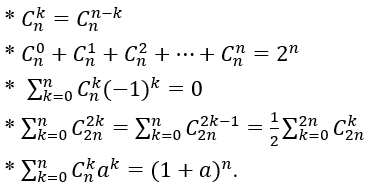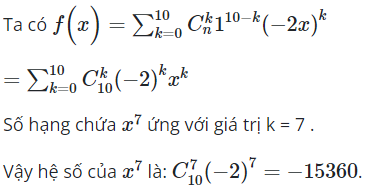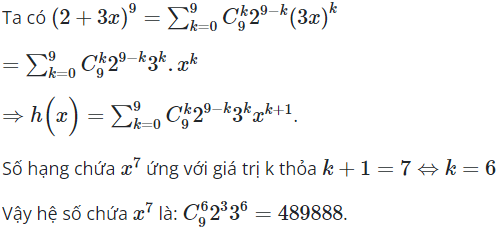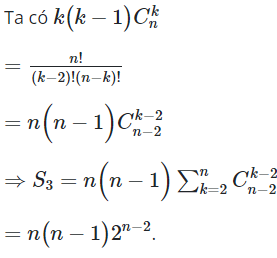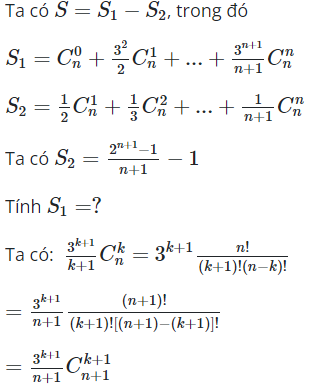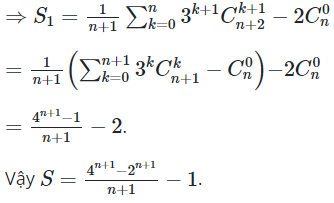Trắc nghiệm Nhị thức Niu-tơn (có đáp án)
Trắc nghiệm Toán 11 Bài 3: Nhị thức Niu-tơn
-
963 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Trong khai triển , hệ số của số hạng chính giữa là:
 Xem đáp án
Xem đáp án
Chọn D.
Trong khai triển có tất cả 11 số hạng nên số hạng chính giữa là số hạng thứ .
Vậy hệ số của số hạng chính giữa là
Câu 2:
06/11/2024Trong khai triển là:
 Xem đáp án
Xem đáp án
Đáp án đúng là A.
Lời giải
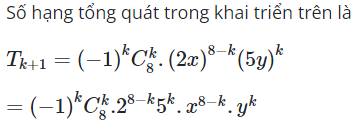
Yêu cầu bài toán xảy ra khi . Khi đó hệ số của số hạng chứa ![]()
*Phuơng pháp giải
Dạng 1. Tìm số hàng chứa xm trong khai triển
Phương pháp giải:
* Với khai triển (axp + bxq)n (p, q là các hằng số)
Ta có: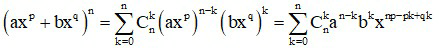
Số hạng chứa xm ứng với giá trị k thỏa mãn: np – pk + qk = m
Từ đó tìm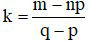
Vậy hệ số của số hạng chứa xm là: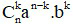
* Với khai triển P(x) = (a + bxp + cxq)n (p, q là các hằng số)
Ta có: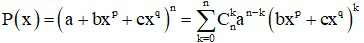
Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm.
* Chú ý:
- Nếu k không nguyên hoặc k > n thì trong khai triển không chứa xm, hệ số phải tìm bằng 0.
- Nếu hỏi hệ số không chứa x tức là tìm hệ số chứa x0.
Dạng 2. Bài toán tính tổng
Phương pháp giải:
Dựa vào khai triển nhị thức Niu tơn
.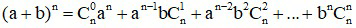
Ta chọn những giá trị a, b thích hợp thay vào đẳng thức trên.
Một số kết quả ta thường hay sử dụng:
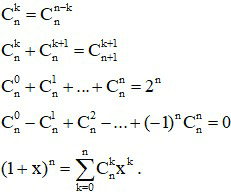
*Lý thuyết
a) Định nghĩa:
b) Nhận xét:
Trong khai triển Niu tơn (a + b)n có các tính chất sau
- Gồm có n + 1 số hạng
- Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n
- Tổng các số mũ của a và b trong mỗi số hạng bằng n
- Các hệ số có tính đối xứng: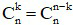
- Quan hệ giữa hai hệ số liên tiếp: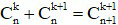
- Số hạng tổng quát thứ k + 1 của khai triển: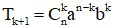
Ví dụ: Số hạng thứ nhất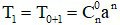
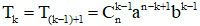
c) Hệ quả:
Ta có :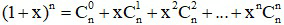
Từ khai triển này ta có các kết quả sau
Xem thêm
Lý thuyết Nhị thức Newton (công thức, khai triển) các dạng bài tập và cách giải
TOP 40 câu Trắc nghiệm Nhị Thức Newton (có đáp án ) | Toán 11
Câu 3:
06/11/2024Trong khai triển , hệ số của số hạng thứ 3 bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là B.
Lời giải
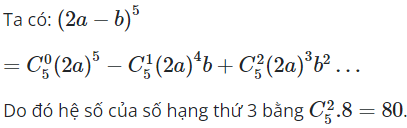
*Phuơng pháp giải
Dạng 1. Tìm số hàng chứa xm trong khai triển
Phương pháp giải:
* Với khai triển (axp + bxq)n (p, q là các hằng số)
Ta có: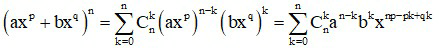
Số hạng chứa xm ứng với giá trị k thỏa mãn: np – pk + qk = m
Từ đó tìm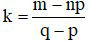
Vậy hệ số của số hạng chứa xm là: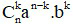
* Với khai triển P(x) = (a + bxp + cxq)n (p, q là các hằng số)
Ta có: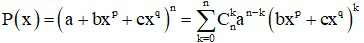
Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm.
* Chú ý:
- Nếu k không nguyên hoặc k > n thì trong khai triển không chứa xm, hệ số phải tìm bằng 0.
- Nếu hỏi hệ số không chứa x tức là tìm hệ số chứa x0.
Dạng 2. Bài toán tính tổng
Phương pháp giải:
Dựa vào khai triển nhị thức Niu tơn
.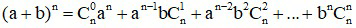
Ta chọn những giá trị a, b thích hợp thay vào đẳng thức trên.
Một số kết quả ta thường hay sử dụng:
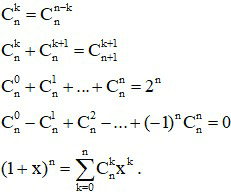
*Lý thuyết
a) Định nghĩa:
b) Nhận xét:
Trong khai triển Niu tơn (a + b)n có các tính chất sau
- Gồm có n + 1 số hạng
- Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n
- Tổng các số mũ của a và b trong mỗi số hạng bằng n
- Các hệ số có tính đối xứng: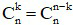
- Quan hệ giữa hai hệ số liên tiếp: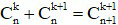
- Số hạng tổng quát thứ k + 1 của khai triển: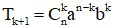
Ví dụ: Số hạng thứ nhất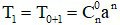
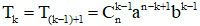
c) Hệ quả:
Ta có :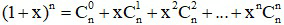
Từ khai triển này ta có các kết quả sau
Xem thêm
Lý thuyết Nhị thức Newton (công thức, khai triển) các dạng bài tập và cách giải
TOP 40 câu Trắc nghiệm Nhị Thức Newton (có đáp án ) | Toán 11
Câu 4:
16/07/2024Trong khai triển nhị thức , . Có tất cả 17 số hạng. Vậy n bằng:
 Xem đáp án
Xem đáp án
Chọn C.
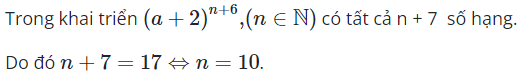
Câu 12:
06/11/2024Trong khai triển , số hạng thứ tư là:
 Xem đáp án
Xem đáp án
Đáp án đúng là D.
Lời giải

*Phuơng pháp giải
Dạng 1. Tìm số hàng chứa xm trong khai triển
Phương pháp giải:
* Với khai triển (axp + bxq)n (p, q là các hằng số)
Ta có: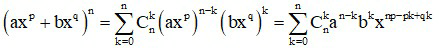
Số hạng chứa xm ứng với giá trị k thỏa mãn: np – pk + qk = m
Từ đó tìm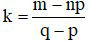
Vậy hệ số của số hạng chứa xm là: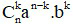
* Với khai triển P(x) = (a + bxp + cxq)n (p, q là các hằng số)
Ta có: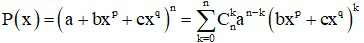
Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm.
* Chú ý:
- Nếu k không nguyên hoặc k > n thì trong khai triển không chứa xm, hệ số phải tìm bằng 0.
- Nếu hỏi hệ số không chứa x tức là tìm hệ số chứa x0.
Dạng 2. Bài toán tính tổng
Phương pháp giải:
Dựa vào khai triển nhị thức Niu tơn
.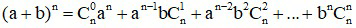
Ta chọn những giá trị a, b thích hợp thay vào đẳng thức trên.
Một số kết quả ta thường hay sử dụng:
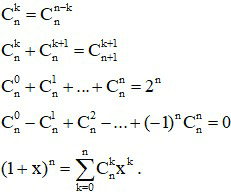
*Lý thuyết
a) Định nghĩa:
b) Nhận xét:
Trong khai triển Niu tơn (a + b)n có các tính chất sau
- Gồm có n + 1 số hạng
- Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n
- Tổng các số mũ của a và b trong mỗi số hạng bằng n
- Các hệ số có tính đối xứng: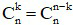
- Quan hệ giữa hai hệ số liên tiếp: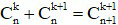
- Số hạng tổng quát thứ k + 1 của khai triển: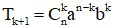
Ví dụ: Số hạng thứ nhất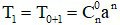
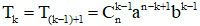
c) Hệ quả:
Ta có :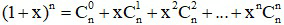
Từ khai triển này ta có các kết quả sau
Xem thêm
Lý thuyết Nhị thức Newton (công thức, khai triển) các dạng bài tập và cách giải
TOP 40 câu Trắc nghiệm Nhị Thức Newton (có đáp án ) | Toán 11
Câu 17:
23/07/2024Số hạng chính giữa trong khai triển là
 Xem đáp án
Xem đáp án
Chọn D.
Số hạng chính giữa trong khai triển trên là số hạng thứ ba:
![]()
Câu 21:
16/07/2024Tìm hệ số của trong khai triển đa thức của
 Xem đáp án
Xem đáp án
Chọn A.
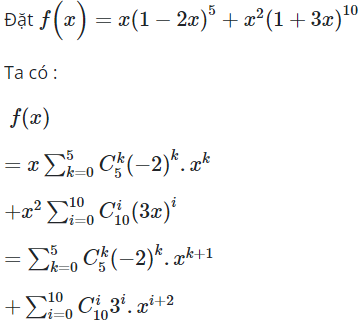
Vậy hệ số của trong khai triển đa thức của ứng với k = 4 và i = 3 là:
![]()
Câu 24:
07/11/2024Tính giá trị của tổng bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là A.
Lời giải
![]()
*Phương pháp giải:
Phương pháp 1: Dựa vào khai triển nhị thức Newton
Ta chọn những giá trị a,b thích hợp thay vào đẳng thức trên.
Một số kết quả ta thường hay sử dụng:
Phương pháp 2: Dựa vào đẳng thức đặc trưng
Mẫu chốt của cách giải trên là ta tìm ra được đẳng thức (*) và ta thường gọi (*) là đẳng thức đặc trưng.
Cách giải ở trên được trình bày theo cách xét số hạng tổng quát ở vế trái (thường có hệ số chứa k) và biến đổi số hạng đó có hệ số không chứa k hoặc chứa k nhưng tổng mới dễ tính hơn hoặc đã có sẵn.
*Lý thuyết:
Với là những số thực tùy ý và với mọi số tự nhiên , ta có:
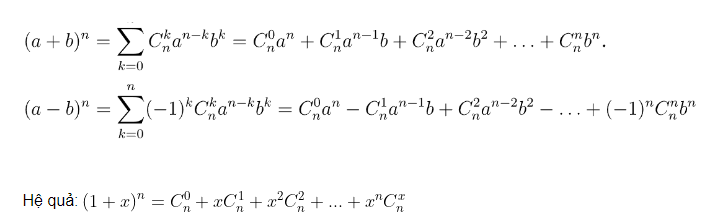
•
•
Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) ứng với n = 4 và n = 5.
Chú ý:
– Các hệ số trong khai triển nhị thức Newton (a + b)n với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.
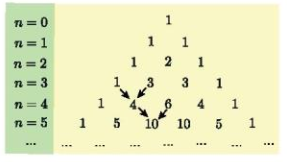
Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của 2 số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).
Bảng số trên dược gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 – 1662).
Xem thêm
Lý thuyết Nhị thức Newton (công thức, khai triển) các dạng bài tập và cách giải
TOP 40 câu Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp (có đáp án ) – Toán 11
Câu 25:
22/07/2024Khai triển rồi thay x , y bởi các giá trị thích hợp. Tính tổng
 Xem đáp án
Xem đáp án
Chọn A.

Câu 28:
16/07/2024Tìm hệ số của trong khai triển biểu thức sau:
 Xem đáp án
Xem đáp án
Chọn A.
Hệ số của trong khai triển ![]()
Hệ số của trong khai triển ![]()
![]()
Hệ số của trong khai triển ![]()
Vậy hệ số chứa thành đa thức là: 29.
Có thể bạn quan tâm
- Trắc nghiệm Nhị thức Niu-tơn (có đáp án) (962 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 3 (Có đáp án): Nhị thức Niu-tơn (312 lượt thi)
- Trắc nghiệm Nhị thức Niu tơn có đáp án (Phần 2) (411 lượt thi)
- Trắc nghiệm Nhị thức Niu-tơn có đáp án (Nhận biết) (444 lượt thi)
- Trắc nghiệm Nhị thức Niu-tơn có đáp án (Thông hiểu) (862 lượt thi)
- Trắc nghiệm Nhị thức Niu-tơn có đáp án (Vận dụng) (371 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản (P1) (2017 lượt thi)
- 100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao (P1) (1511 lượt thi)
- Trắc nghiệm Hoán vị - Chỉnh hợp - Tổ hợp (có đáp án) (929 lượt thi)
- Trắc nghiệm Hoán vị - Chỉnh hợp - Tổ hợp có đáp án (Thông hiểu) (815 lượt thi)
- Trắc nghiệm Quy tắc đếm có đáp án (Thông hiểu) (788 lượt thi)
- Trắc nghiệm Quy tắc đếm (có đáp án) (747 lượt thi)
- Trắc nghiệm Phép thử và biến cố (có đáp án) (744 lượt thi)
- Trắc nghiệm Xác suất của biến cố (có đáp án) (675 lượt thi)
- Trắc nghiệm tổng hợp Chương 2 : Tổ hợp - Xác suất có đáp án (Phần 1) (665 lượt thi)
- Trắc nghiệm Biến ngẫu nhiên rời rạc có đáp án (Nhận biết) (570 lượt thi)