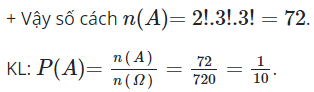Trắc nghiệm Xác suất của biến cố (có đáp án)
Trắc nghiệm Toán 11 Bài 5: Xác suất của biến cố
-
759 lượt thi
-
23 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng ?
 Xem đáp án
Xem đáp án
Chọn B
Loại trừ :A ;B ;C đều sai
Câu 2:
23/07/2024Gieo đồng tiền hai lần. Xác suất để sau hai lần gieo thì mặt sấp xuất hiện ít nhất một lần
 Xem đáp án
Xem đáp án
Chọn C.
Số phần tử không gian mẫu: n(Ω)=2.2=4
Biến cố xuất hiện mặt sấp ít nhất một lần: ![]()
![]()
Câu 3:
19/07/2024Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một lần xuất hiện mặt sấp là:
 Xem đáp án
Xem đáp án
Chọn A.
Phép thử : Gieo đồng tiền 5 lần cân đối và đồng chất
![]()
Biến cố A : Được ít nhất một lần xuất hiện mặt sấp
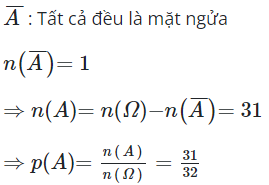
Câu 4:
23/07/2024Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một đồng tiền xuất hiện mặt sấp là
 Xem đáp án
Xem đáp án
Chọn A.
![]()
A : “được ít nhất một đồng tiền xuất hiện mặt sấp”.
Xét biến cố đối A: “không có đồng tiền nào xuất hiện mặt sấp”.
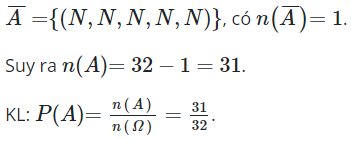
Câu 5:
22/07/2024Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần gieo đều xuất hiện mặt sấp là:
 Xem đáp án
Xem đáp án
Chọn đáp án: C.
Gọi A là biến cố: “cả bốn lần gieo đều xuất hiện mặt sấp.”

Câu 6:
20/07/2024Một con súc sắc đồng chất được đổ 6 lần. Xác suất để được một số lớn hơn hay bằng 5 xuất hiện ít nhất 5 lần là
 Xem đáp án
Xem đáp án

Vậy xác suất để được một số lớn hơn hay bằng 5 xuất hiện ít nhất 5 lần là
![]()
Câu 7:
21/07/2024Gieo ngẫu nhiên hai con súc sắc cân đối, đồng chất. Xác suất của biến cố “Tổng số chấm của hai con súc sắc bằng 6” là
 Xem đáp án
Xem đáp án
Chọn D.
Gọi A là biến cố: “Tổng số chấm của hai con súc sắc bằng 6.”

Câu 8:
22/07/2024Gieo hai con súc sắc. Xác suất để tổng số chấm trên hai mặt chia hết cho 3 là:
 Xem đáp án
Xem đáp án
Chọn C.

Câu 10:
22/07/2024Gieo một con súc sắc 3 lần. Xác suất để được mặt số hai xuất hiện cả 3 lần là:
 Xem đáp án
Xem đáp án
Chọn D.
Số phần tử không gian mẫu: n(Ω)=6.6.6=216
Số phần tử của biến cố xuất hiện mặt số hai ba lần:
![]()
Câu 11:
22/07/2024Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá ách (A) hay lá rô là:
 Xem đáp án
Xem đáp án
Chọn C.
Số phần tử không gian mẫu: ![]()
Số phần tử của biến cố xuất hiện lá ách hay lá rô: ![]()
![]()
Câu 12:
23/07/2024Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá bồi (J) màu đỏ hay lá 5 là:
 Xem đáp án
Xem đáp án
Chọn B.
Số phần tử không gian mẫu: ![]()
Số phần tử của biến cố xuất hiện lá bồi đỏ hay lá 5: ![]()
![]()
Câu 13:
23/07/2024Một túi chứa 2 bi trắng và 3 bi đen. Rút ra 3 bi. Xác suất để được ít nhất 1 bi trắng là:
 Xem đáp án
Xem đáp án
Chọn C.
Số phần tử của không gian mẫu: n(Ω)=C35=10
Số khả năng để có không có bi trắng là: ![]()
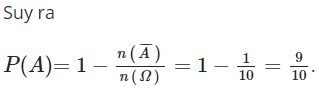
Câu 14:
23/07/2024Một hộp đựng 4 bi xanh và 6 bi đỏ lần lượt rút 2 viên bi. Xác suất để rút được một bi xanh và 1 bi đỏ là:
 Xem đáp án
Xem đáp án
Chọn D.

Câu 15:
22/07/2024Một bình đựng 5 quả cầu xanh và 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để được 3 quả cầu khác màu là:
 Xem đáp án
Xem đáp án
Chọn C.

Câu 16:
16/07/2024Có hai hộp đựng bi. Hộp I có 9 viên bi được đánh số 1, 2, …, 9. Lấy ngẫu nhiên mỗi hộp một viên bi. Biết rằng xác suất để lấy được viên bi mang số chẵn ở hộp II là 310. Xác suất để lấy được cả hai viên bi mang số chẵn là:
 Xem đáp án
Xem đáp án
Chọn B.
Gọi X là biến cố: “lấy được cả hai viên bi mang số chẵn. “
Gọi A là biến cố: “lấy được viên bi mang số chẵn ở hộp I “
![]()
Gọi B là biến cố: “lấy được viên bi mang số chẵn ở hộp II “ P(B)=310.
Ta thấy biến cố A, B là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có: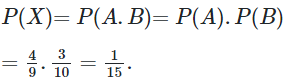
Câu 17:
21/07/2024Một hộp chứa 5 viên bi màu trắng, 15 viên bi màu xanh và 35 viên bi màu đỏ. Lấy ngẫu nhiên từ hộp ra 7 viên bi. Xác suất để trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ là:
 Xem đáp án
Xem đáp án
Chọn B.
Gọi A là biến cố: “trong số viên bi được lấy ra có ít nhất 1 viên bi màu đỏ.”
-Không gian mẫu: C755.
- A là biến cố: “trong số 7 viên bi được lấy ra không có viên bi màu đỏ nào.”
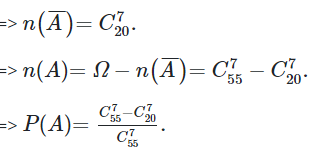
Câu 18:
23/07/2024Có 3 chiếc hộp. Hộp A chứa 3 bi đỏ, 5 bi trắng. Hộp B chứa 2 bi đỏ, hai bi vàng. Hộp C chứa 2 bi đỏ, 3 bi xanh. Lấy ngẫu nhiên một hộp rồi lấy một bi từ hộp đó. Xác suất để được một bi đỏ là:
 Xem đáp án
Xem đáp án
Chọn D.

Gọi C là biến cố “ lấy ngẫu nhiên một hộp, trong hộp đó lại lấy ngẫu nhiên một viên bi và được bi đỏ ” là ![]()
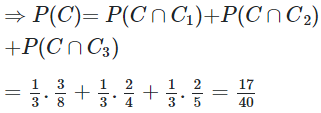
Câu 19:
17/07/2024Một hộp chứa 3 bi đỏ, 2 bi vàng và 1 bi xanh. Lần lượt lấy ra ba bi và không bỏ lại. Xác suất để được bi thứ nhất đỏ, nhì xanh, ba vàng là:
 Xem đáp án
Xem đáp án
Chọn B.
Xác suất để được bi thứ nhất đỏ, nhì xanh, ba vàng là: 3.1.26.5.4=120
Câu 20:
22/07/2024Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn không có nữ nào cả.
 Xem đáp án
Xem đáp án
Chọn C.
n(Ω)=C210=45
Gọi :”2 người được chọn không có nữ” thì :”2 người được chọn đều là nam”.
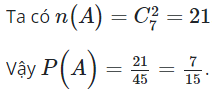
Câu 21:
17/07/2024Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có ít nhất một nữ.
 Xem đáp án
Xem đáp án
Chọn D.
![]()
Gọi A :”2 người được chọn có ít nhất 1 nữ” thì AˉA :”2 người được chọn không có nữ” hay

Câu 22:
17/07/2024Sắp quyển sách Toán và quyển sách Vật Lí lên một kệ dài. Xác suất để quyển sách cùng một môn nằm cạnh nhau là:
 Xem đáp án
Xem đáp án
Chọn B.
Phép thử : Sắp ba quyển toán, ba quyển lí lên kệ dài
n(Ω)=6!=720
Biến cố A : Có hai quyển sách cùng môn nằm cạnh nhau
A: Các quyển sách cùng môn không nằm cạnh nhau
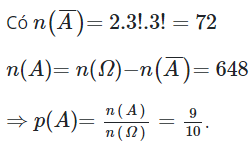
Có thể bạn quan tâm
- Trắc nghiệm Xác suất của biến cố (có đáp án) (758 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 5 (Có đáp án): Xác suất của biến cố (496 lượt thi)
- Trắc nghiệm Xác suất của biến cố có đáp án (Phần 2) (572 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản (P1) (2358 lượt thi)
- 100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao (P1) (1793 lượt thi)
- Trắc nghiệm Hoán vị - Chỉnh hợp - Tổ hợp (có đáp án) (1068 lượt thi)
- Trắc nghiệm Nhị thức Niu-tơn (có đáp án) (1055 lượt thi)
- Trắc nghiệm Nhị thức Niu-tơn có đáp án (Thông hiểu) (949 lượt thi)
- Trắc nghiệm Hoán vị - Chỉnh hợp - Tổ hợp có đáp án (Thông hiểu) (904 lượt thi)
- Trắc nghiệm Quy tắc đếm có đáp án (Thông hiểu) (871 lượt thi)
- Trắc nghiệm Phép thử và biến cố (có đáp án) (857 lượt thi)
- Trắc nghiệm Quy tắc đếm (có đáp án) (824 lượt thi)
- Trắc nghiệm tổng hợp Chương 2 : Tổ hợp - Xác suất có đáp án (Phần 1) (789 lượt thi)