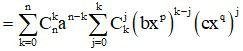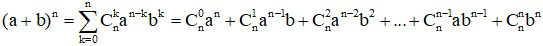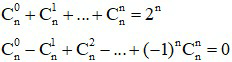Trong khai triển ${\left(0,2+0,8\right)}^5$, số hạng thứ tư là:

Đáp án đúng là D.

Lời giải

*Phuơng pháp giải

Dạng 1. Tìm số hàng chứa x^m trong khai triển

Phương pháp giải:

* Với khai triển (ax^p + bx^q)ⁿ (p, q là các hằng số)

Ta có: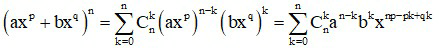 

Số hạng chứa x^m ứng với giá trị k thỏa mãn: np – pk + qk = m 

Từ đó tìm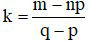 

Vậy hệ số của số hạng chứa x^m là: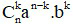với giá trị k đã tìm được ở trên.

* Với khai triển P(x) = (a + bx^p + cx^q)ⁿ (p, q là các hằng số)

Ta có: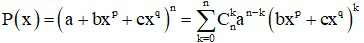 

Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của x^m.

* Chú ý:

- Nếu k không nguyên hoặc k > n thì trong khai triển không chứa x^m, hệ số phải tìm bằng 0.

- Nếu hỏi hệ số không chứa x tức là tìm hệ số chứa x⁰.

Dạng 2. Bài toán tính tổng

Phương pháp giải:

Dựa vào khai triển nhị thức Niu tơn

. 

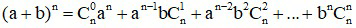
Ta chọn những giá trị a, b thích hợp thay vào đẳng thức trên.

Một số kết quả ta thường hay sử dụng:

 

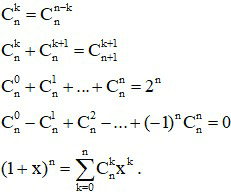
*Lý thuyết

a) Định nghĩa: 

b) Nhận xét:

Trong khai triển Niu tơn (a + b)ⁿ có các tính chất sau

- Gồm có n + 1 số hạng

- Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n

- Tổng các số mũ của a và b trong mỗi số hạng bằng n

- Các hệ số có tính đối xứng: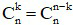 

- Quan hệ giữa hai hệ số liên tiếp: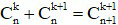 

- Số hạng tổng quát thứ k + 1 của khai triển: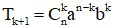 

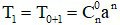
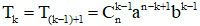
Ví dụ: Số hạng thứ nhất, số hạng thứ k: 

c) Hệ quả:

Ta có :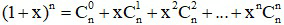 

Từ khai triển này ta có các kết quả sau

Xem thêm

Lý thuyết Nhị thức Newton (công thức, khai triển) các dạng bài tập và cách giải 

TOP 40 câu Trắc nghiệm Nhị Thức Newton (có đáp án ) | Toán 11