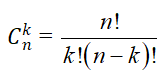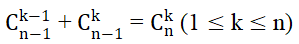Câu hỏi:
25/11/2024 1,323Có 100 tấm thẻ được đánh số từ 1 đến 100. Lấy ngẫu nhiên 5 thẻ. Tính số phần tử của biến cố B: “ Có ít nhất một số ghi trên thẻ được chọn chia hết cho 3”.
A. 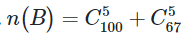
B. 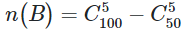
C. 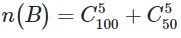
D. 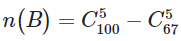
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là D.
Lời giải
Từ 1 đến 100 có 33 số chia hết cho 3. Do đó, số cách chọn 5 tấm thẻ mà không có tấm thẻ nào ghi số chia hết cho 3 là:
![]()
![]()
*Phương pháp giải:
Dùng phương pháp biến cố đối:
- Xác định số cách chọn mà cả lần đều không có tấm thẻ nào chia hết cho
- Số phần tử của là
*Lý thuyết:
a) Định nghĩa:
- Giả sử A có n phần tử (n ≥ 1). Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).
- Quy ước: Tổ hợp chập 0 của n phần tử là tập rỗng.
b) Số các tổ hợp:
- Kí hiệu Cnk là số các tổ hợp chập k của n phần tử (0 ≤ k ≤ n).
- Định lý:
c) Tính chất của các số Cnk
- Tính chất 1:
Cnk = Cnn - k (0 ≤ k ≤ n)
- Tính chất 2:
Xem thêm
Lý thuyết Tổ hợp - xác suất hay, chi tiết
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Gieo ngẫu nhiên 2 đồng tiền thì không gian mẫu của phép thử có bao nhiêu biến cố:
Câu 2:
Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của biến cố: C: “ 4 viên bi lấy ra có đủ 3 màu”
Câu 3:
Một xạ thủ bắn liên tục 4 phát đạn vào bia. Gọi
A: “Lần thứ tư mới bắn trúng bia’’
Câu 4:
Có 100 tấm thẻ được đánh số từ 1 đến 100. Lấy ngẫu nhiên 5 thẻ. Tính số phần tử của biến cố A: “ Số ghi trên các tấm thẻ được chọn là số chẵn”
Câu 5:
Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện đúng 1 lần là:
Câu 6:
Gieo 2 con súc sắc và gọi kết quả xảy ra là tích số hai nút ở mặt trên. Số phần tử của không gian mẫu là:
Câu 7:
Một hộp đựng 10 thẻ, đánh số từ 1 đến 10. Chọn ngẫu nhiên thẻ. Gọi A là biến cố để tổng số của 3 thẻ được chọn không vượt quá 8. Số phần tử của biến cố là:
Câu 8:
Xét phép thử tung con súc sắc 6 mặt hai lần. Xác định số phần tử của không gian mẫu
Câu 9:
Cho phép thử có không gian mẫu . Các cặp biến cố không đối nhau là:
Câu 10:
Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của không gian mẫu:
Câu 11:
Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:
Câu 12:
Gieo một đồng tiền và một con súcsắc. Số phần tử của không gian mẫu là:
Câu 13:
Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của biến cố: A: “ 4 viên bi lấy ra có đúng hai viên bi màu trắng”:
Câu 14:
Gieo con súc sắc hai lần. Biến cố A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm :
Câu 15:
Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là: