Trắc nghiệm ôn tập chương 3 (có đáp án)
Trắc nghiệm Toán 7 Bài ôn tập chương 3
-
318 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
18/07/2024Chọn câu đúng. Cho tam giác ABC vuông tại B theo định lí Pytago ta có:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta có:
AC2=AB2+BC2
Câu 2:
21/07/2024Cho △MNP có ˆM=40°, các đường phân giác NH và PK của góc N và góc P cắt nhau tại I. Khi đó góc NIP bằng:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
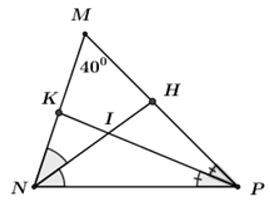
Xét có (định lí tổng ba góc trong một tam giác)
Vì NH là phân giác của
(2) (tính chất tia phân giác)
Vì PK là phân giác của
(3) (tính chất tia phân giác)
Từ (1)(2) và (3)
(*)
Xét có: (**) (định lí tổng ba góc trong tam giác)
Từ (*) và (**)
Câu 3:
18/07/2024Chọn đáp án đúng nhất. Tam giác ABC có thì tam giác ABC là tam giác:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Xét tam giác ABC có nên tam giác ABC cân tại A.
Mà tam giác này cân có một góc bằng 600 nên tam giác ABC là tam giác đều.
Câu 4:
22/07/2024Tam giác cân có góc ở đỉnh là 800. Số đo góc ở đáy là:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Gỉa sử tam giác ABC cân tại A có: .
Ta sẽ tìm số đo góc B hoặc góc C
Áp dụng định lí tổng ba góc trong tam giác ta có:
Do đó tam giác ABC cân tại A nên . Từ đó suy ra:
Vậy số đo ở đáy là 500.
Câu 5:
18/07/2024Cho tam giác ABC có: , khi đó tam giác:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Áp dụng định lí tổng ba góc trong tam giác ta có:
Tam giác ABC có: nên áp dụng quan hệ giữa cạnh và góc trong tam giác suy ra AC > BC > AB
Câu 6:
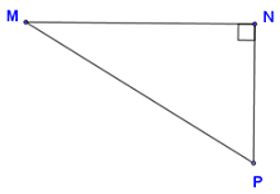
19/07/2024Cho tam giác vuông MNP như hình vẽ. Trực tam giác MNP là
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Ta có: nên MN;NP là các đường cao của tam giác MNP mà hai đường này giao nhau tại N nên N là trực tâm tam giác MNP
Câu 7:
23/07/2024Cho tam giác ABC vuông tại A có AB = 5cm, AC = 12cm. Gọi G là trọng tâm tam giác ABC, khi đó GA + GB + GC bằng (làm tròn đến 2 chữ số sau dấu phẩy)
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
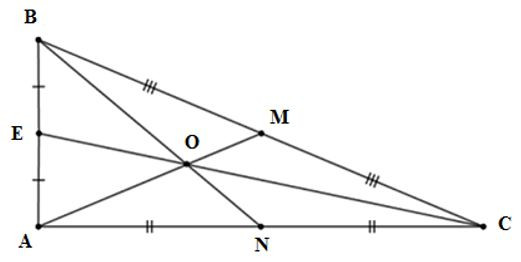
Gọi AM, BN, CE là ba đường trung tuyến của tam giác ABC
vuông tại A nên theo định lí Pytago ta có:
Ta có: AM, BN, CE là các đường trung tuyến ứng với các cạnh BC, AC, AB của tam giác vuông ABC
Suy ra M, N, E lần lượt là trung điểm của các cạnh BC, AC, AB
Áp dụng định lí Pytago với tam giác AEC vuông tại A ta có:
Ta có tam giác ABC vuông tại A, AM là đường trung tuyến ứng với cạnh huyền BC nên ta có:
Ta có:
(do G là trọng tâm tam giác ABC)
Câu 8:
20/07/2024Cho tam giác ABC có AB = 15cm, BC = 8cm. Tính độ dài cạnh AC biết độ dài này (theo đơn vị cm) là một số nguyên tố lớn hơn bình phương của 4
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Theo bất đẳng thức tam giác ABC có: AB – BC < AC < AB + BC
Suy ra 15 – 8 < AC < 15 + 8 hay 7 < AC < 23.
Theo đề bài ta có: AC là số nguyên tố và AC > 42 = 16
Suy ra AC = 17cm hoặc AC = 19cm
+) Nếu AC = 17cm thì 15 + 8 >17 (thỏa mãn bất đẳng thức tam giác)
+) Nếu AC = 19cm thì 15 + 8 > 19 (thỏa mãn bất đẳng thức tam giác)
Vậy độ dài cạnh AC có thể là 17 cm và 19 cm
Câu 9:
20/07/2024Cho tam giác MON, trung tuyến MI, biết và . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
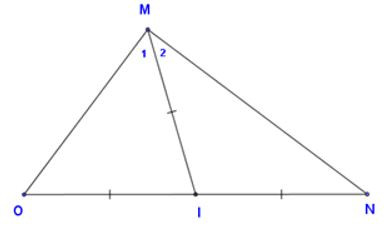
Vì
Xét tam giác MIO có nên tam giác MIO cân tại I (tính chất tam giác cân)
Xét tam giác MIN có nên tam giác MIN cân tại I (tính chất tam giác cân)
Suy ra
Xét tam giác MON có: (định lí tổng ba góc trong tam giác)
Suy ra nên tam giác MON vuông tại M
Câu 10:
20/07/2024Cho hình vẽ. Biết . Tính
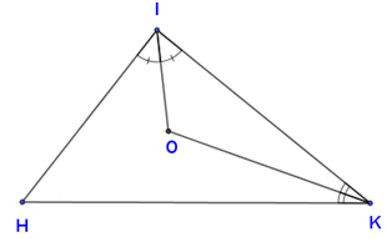
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
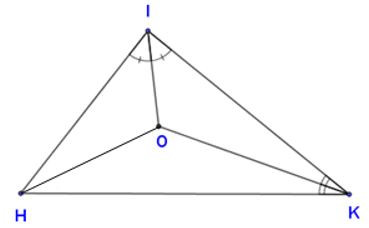
Ta có:
là tia phân giác góc KIH (1)
Ta có:
là tia phân giác góc IKH (2)
Từ (1) và (2) suy ra O là giao điểm hai tia phân giác
Do đó O thuộc tia phân giác của góc H (tính chất ba đường phân giác trong tam giác)
Suy ra: (tính chất đường phân giác)
Câu 11:
18/07/2024Chọn đáp án đúng. Cho tam giác ABC có đường cao AH. Biết B nằm giữa H và C. Ta có:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
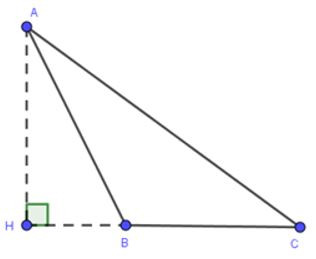
Vì là góc ngoài tại đỉnh B của tam giác AHB nên:
Hay nên là góc tù và là góc lớn nhất trong tam giác ABC
Câu 12:
20/07/2024Cho vuông tại A có AB = 4cm, BC = 5cm. So sánh các góc của tam giác ABC
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Vì tam giác ABC vuông tại A nên theo định lí Pytago có:
Từ đó ta có: suy ra
Câu 13:
23/07/2024Cho tam giác MNP cân ở M, trung tuyến MA, trọng tâm G.
Biết MN = 13cm, NA = 12cm. Khi đó độ dài MG là:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
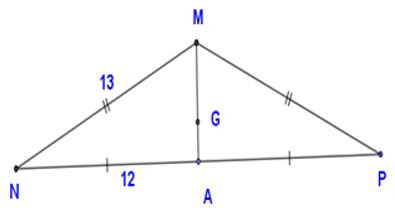
Vì cân tại M có MA là trung tuyến nên MA cũng là đường cao (tính chất các đường trong tam giác cân)
Xét vuông tại A, theo định lí Pytago ta có:
Vì MA là trung tuyến, G là trọng tâm nên tính chất trọng tâm tam giác ta có:
Câu 14:
18/07/2024Cho tam giác ABC, biết số đo các góc tỉ lệ với nhau theo tỉ số: . Hãy so sánh ba cạnh của tam giác ABC
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
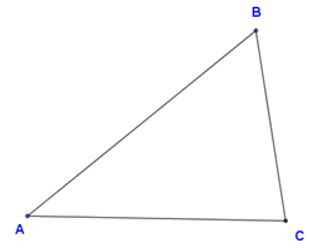
Theo bài ra ta có:
Suy ra AB > AC > BC (quan hệ giữa góc và cạnh đối diện trong )
Câu 15:
23/07/2024Cho tam giác ABC vuông tại A có BD là phân giác góc ABD (D thuộc AC), kẻ DE vuông góc với BC (E thuộc BC). Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
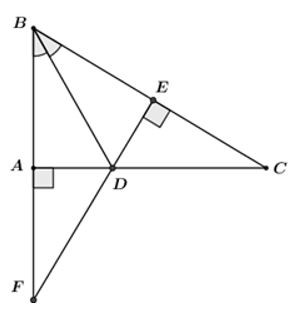
+) DE vuông góc với BC nên ta có tam giác BDE là tam giác vuông
Xét hai tam giác vuông BAD và BED ta có:
(do BD là tia phân giác của góc B)
BD là cạnh chung
Vậy (cạnh huyền - góc nhọn)
(các cặp cạnh tương ứng)
nằm trên đường trung trực của AE và BD là đường trung trực của AE. Do đó A đúng
+) Xét hai tam giác vuông ADF và EDC ta có:
AF = EC (gt)
DA = DE (cmt)
Vậy (hai cạnh góc vuông bằng nhau)
Suy ra DF = DC (hai cạnh tương ứng). Do đó B đúng
+)Trong tam giác vuông ADF, AD là cạnh góc vuông, DF là cạnh huyền nên
Mà (cmt). Từ đó, suy ra . Do đó C đúng
Vậy cả A, B, C đều đúng
Có thể bạn quan tâm
- Trắc nghiệm ôn tập chương 3 (có đáp án) (317 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Tính chất ba đường trung trực của tam giác (có đáp án) (603 lượt thi)
- Trắc nghiệm Quan hệ giữa góc và cạnh đối diện trong tam giác (có đáp án) (411 lượt thi)
- Trắc nghiệm Tính chất đường trung trực của một đoạn thẳng (có đáp án) (401 lượt thi)
- Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác (có đáp án) (397 lượt thi)
- Trắc nghiệm Tính chất ba đường cao của tam giác (có đáp án) (388 lượt thi)
- Trắc nghiệm Tính chất ba đường phân giác của tam giác (có đáp án) (385 lượt thi)
- Trắc nghiệm Tính chất ba đường trung tuyến trong tam giác (có đáp án) (371 lượt thi)
- Trắc nghiệm Tính chất tia phân giác của một góc (có đáp án) (368 lượt thi)
- Trắc nghiệm Quan hệ giữa đường vuông góc và đường xiên. Đường xiên và hình chiếu của đường xiên (có đáp án) (365 lượt thi)
