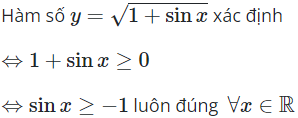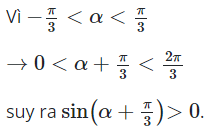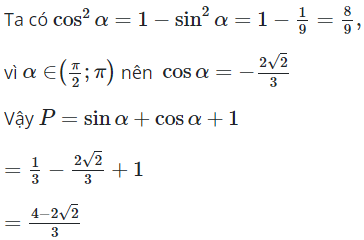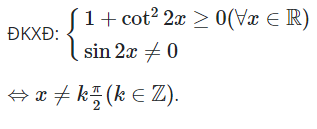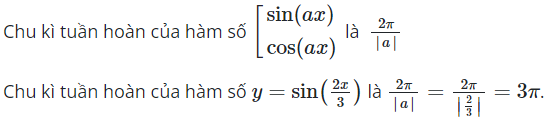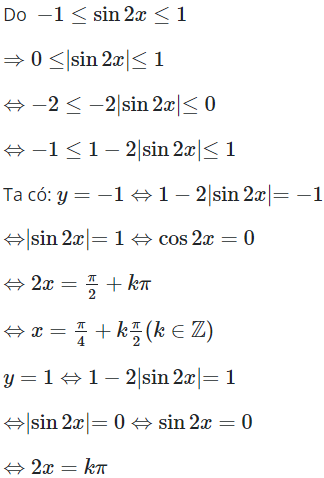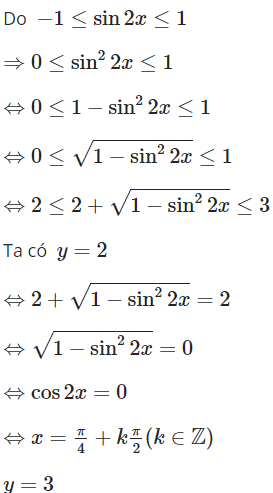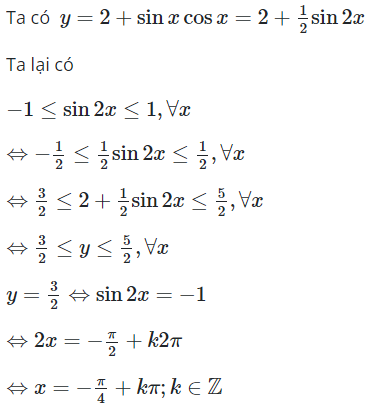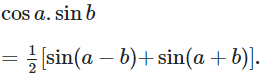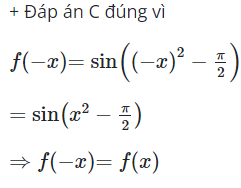Trắc nghiệm Hàm số lượng giác (có đáp án)
Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác
-
1447 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
28/11/2024Cho và .
Mệnh đề nào dưới đây là đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Lời giải
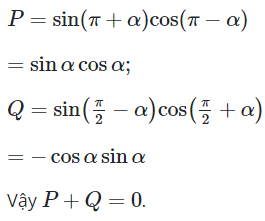
*Phương pháp giải:
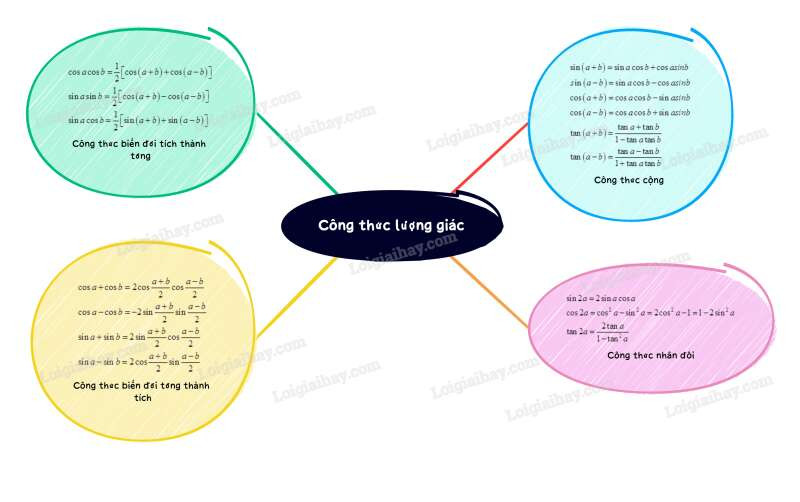
*Lý thuyết
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm
Lý thuyết Công thức lượng giác – Toán 11 Kết nối tri thức
Câu 4:
17/07/2024Giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lượt là
 Xem đáp án
Xem đáp án
Chọn A
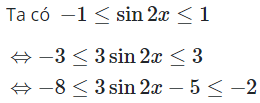
Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lươt là -8 và -2 .
Câu 7:
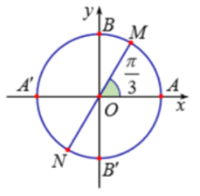
23/07/2024Trên hình vẽ sau các điểm M , N là những điểm biểu diễn của các cung có số đo là:
 Xem đáp án
Xem đáp án
Chọn C
Ta có: Cung có số đo biểu diễn hai điểm M, N có số đo cung lần lượt là
Câu 9:
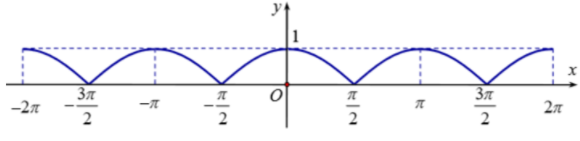
18/07/2024Đồ thị hàm số trên hình vẽ là đồ thị của hàm số nào
 Xem đáp án
Xem đáp án
Chọn C
Nhận xét:
+) thì . Suy ra loại B và D
+) thì y = 0. Suy ra loại A
Vậy đáp án đúng là C.
Câu 15:
07/10/2024Điều kiện xác định của hàm số là
 Xem đáp án
Xem đáp án
Đáp án đúng: B
* Phương pháp giải:
Tìm tập xác định của hàm số lượng giác. Hàm số y =tan sẽ xác định ≠ )
* Lời giải:
Hàm số y=tan2x xác định khi và chỉ khi
2x ≠ x ≠
* Một số phương trình lượng giác thường gặp:
a) Phương trình bậc nhất đối với một hàm số lượng giác
*Phương pháp giải:
Chuyển vế rồi chia hai vế của phương trình dạng at+b=0 (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.
b) Phương trình bậc hai đối với một hàm số lượng giác
*Phương pháp giải:
Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này. Cuối cùng ta đưa về việc giải các phương trình lượng giác cơ bản.
Xem thêm các bài viết liên quan hay, chi tiết:
50 Bài tập Phương trình lượng giác cơ bản Toán 11
100 câu trắc nghiệm Phương trình lượng giác nâng cao
Câu 16:
23/07/2024Tìm mệnh đề đúng trong các mệnh đề sau?
 Xem đáp án
Xem đáp án
Chọn D
Hàm số đồng biến trên mỗi khoảng ![]() và nghịch biến trên mỗi khoảng
và nghịch biến trên mỗi khoảng ![]() với
với
Câu 20:
22/07/2024Giá trị lớn nhất của hàm số là
 Xem đáp án
Xem đáp án
Chọn D
Gọi thỏa mãn phương trình ![]()
Điều kiện để (1) có nghiệm là
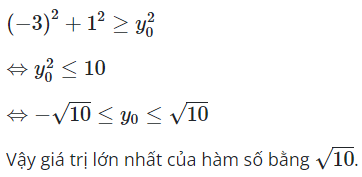
Câu 24:
16/07/2024Giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lượt là
 Xem đáp án
Xem đáp án
Chọn C
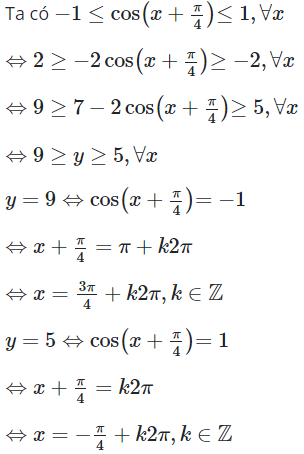
Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lượt là 5 và 9.
Câu 25:
23/07/2024Giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lượt là
 Xem đáp án
Xem đáp án
Chọn D
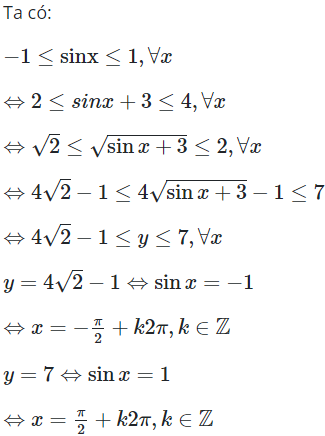
Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lượt là và 7
Câu 26:
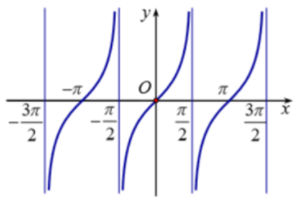
23/07/2024Hàm số nào sau đây đồng biên trên khoảng ?
 Xem đáp án
Xem đáp án
Chọn C
Nhìn vào đồ thị hàm ta thấy trong khoảng đồ thị hàm số là 1 đường cong đi lên. Do vậy, hàm số đồng biến trên khoảng
Câu 27:
16/07/2024Để có đồ thị hàm số , ta thực hiện phép tịnh tiến đồ thị theo véctơ:
 Xem đáp án
Xem đáp án
Chọn C
Ta có: Theo biểu thức tọa độ của phép tịnh tiến 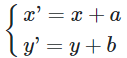
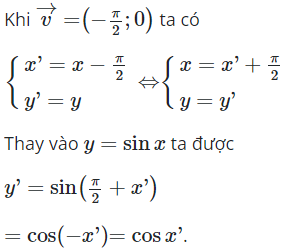
Câu 29:
18/07/2024Chọn khẳng định đúng trong các khẳng định sau:
 Xem đáp án
Xem đáp án
Chọn B
Chu kì tuần hoàn của hàm số ![]()
Có thể bạn quan tâm
- Trắc nghiệm Hàm số lượng giác (có đáp án) (1446 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (394 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (Nhận biết) (528 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (Thông hiểu) (442 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (Vận dụng) (382 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (Phần 2) (371 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Phương trình lượng giác nâng cao (1932 lượt thi)
- 100 câu trắc nghiệm Hàm số lượng giác cơ bản (1363 lượt thi)
- Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án) (823 lượt thi)
- Trắc nghiệm Ôn tập chương 1 (có đáp án) (719 lượt thi)
- Trắc nghiệm Một số phương trình lượng giác thường gặp (có đáp án) (656 lượt thi)
- Một số phương trình lượng giác thường gặp có đáp án (Vận dụng) (591 lượt thi)
- Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Thông hiểu) (589 lượt thi)
- Trắc nghiệm Chương 1: Hàm số lượng giác và phương trình lượng giác có đáp án (589 lượt thi)
- Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Vận dụng) (379 lượt thi)
- Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (378 lượt thi)