Trắc nghiệm Cấp số nhân có đáp án (Nhận biết)
-
311 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Cho cấp số nhân , biết: . Lựa chọn đáp án đúng.
Xem đáp án
Đáp án A
Vì là cấp số nhân nên
Câu 2:
20/07/2024Dãy số 1,2,4,8,16,... là một cấp số nhân với:
Xem đáp án
Đáp án B
Cấp số nhân: 1,2,4,8,16,32,…
Câu 5:
20/07/2024Cho cấp số nhân với . Viết bốn số hạng đầu tiên của cấp số nhân.
Xem đáp án
Đáp án B
Ta có:
Câu 13:
17/07/2024Cho dãy số là một cấp số nhân với . Dãy số nào sau đây không phải là cấp số nhân?
Câu 14:
07/11/2024Cho cấp số nhân có và q = -2. Tính tổng 10 số hạng đầu tiên của cấp số nhân đã cho.
Xem đáp án
Đáp án đúng là D
LỜi giải:
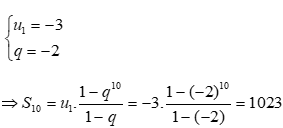
*Phương pháp giải:
Để xác định một cấp số nhân, ta cần xác định số hạng đầu và công bội. Do đó, ta thường biểu diễn giả thiết của bài toán qua u1 và q.
Số hạng tổng quát của cấp số nhân:
un = u1.qn-1, n ≥ 1 .
Trong đó q: công bội của cấp số nhân.
Tính chất:
*Lý thuyết:
- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
- Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi:
un + 1 = un. q với .
- Đặc biệt
Khi q = 0, cấp số nhân có dạng u1, 0, 0, …., 0,…..
Khi q = 1, cấp số nhân có dạng u1, u1, u1, …., u1,…
Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, 0, 0,…, 0..
Nếu cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát un được xác định bởi công thức: un = u1.qn - 1 với n ≥ 2.
Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:
( hay ).
Xem thêm
Lý thuyết Cấp số nhân (mới + Bài Tập) – Toán 11
TOP 40 câu Trắc nghiệm Cấp số nhân (có đáp án ) – Toán 11
