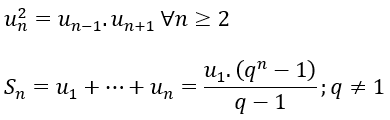Cho cấp số nhân $\left({\mathrm{u}}_{\mathrm{n}}\right)$ có ${\mathrm{u}}_1=-3$ và q = -2. Tính tổng 10 số hạng đầu tiên của cấp số nhân đã cho.

Đáp án đúng là D

LỜi giải:

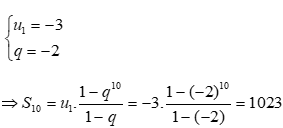
*Phương pháp giải:

Để xác định một cấp số nhân, ta cần xác định số hạng đầu và công bội. Do đó, ta thường biểu diễn giả thiết của bài toán qua u₁ và q.

Số hạng tổng quát của cấp số nhân:

                u_n = u₁.q^n-1, n ≥ 1 .

        Trong đó q: công bội của cấp số nhân.

Tính chất:

*Lý thuyết:

- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.

Số q được gọi là công bội của cấp số nhân.

- Nếu (u_n) là cấp số nhân với công bội q, ta có công thức truy hồi:

u_{n + 1} = u_n. q với $n\in \mathbb{N}*$.

- Đặc biệt

Khi q = 0, cấp số nhân có dạng u₁, 0, 0, …., 0,…..

Khi q = 1, cấp số nhân có dạng u₁, u₁, u₁, …., u₁,…

Khi u₁ = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, 0, 0,…, 0..

Nếu cấp số nhân có số hạng đầu u₁ và công bội q thì số hạng tổng quát u_n được xác định bởi công thức: u_n = u₁.q^{n - 1} với n ≥ 2.

Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:

$u_k^2=u_{k-1}.u_{k+\text{}1};k\ge 2$

( hay $\left|u_k\right|=\sqrt{u_{k-1}.u_{k+\text{}1}}$).

Xem thêm

Lý thuyết Cấp số nhân (mới + Bài Tập) – Toán 11 

TOP 40 câu Trắc nghiệm Cấp số nhân (có đáp án ) – Toán 11