Chọn A

1)  Xét dãy số : $u_n=-\frac{3^{n-1}}{5}$

$\frac{u_{n+1}}{u_n}=-\frac{3^{n+\text{}1-1}}{5}:\left(-\frac{3^{n-1}}{5}\right)=3\Rightarrow \left(u_n\right)$ là cấp số nhân với công bội q= 3.

 (2). Xét dãy số: u_n = 3n - 1

      Ta có: $\frac{u_{n+1}}{u_n}=\frac{3(n+1)-1}{3n-1}=\frac{3n+2}{3n-1}\Rightarrow \left(u_n\right)$ không phải là cấp số  nhân.

( 3) Xét  dãy số : $u_n=\frac{2^n-1}{3}$

Ta có: $\frac{u_{n+1}}{u_n}=\frac{2^{n+1}-1}{2^n-1}\Rightarrow \left(u_n\right)$ không phải là cấp số  nhân

(4) xét dãy số u_n = n³

Ta có: $\frac{u_{n+1}}{u_n}=\frac{{(n+1)}^3}{n^3}\Rightarrow \left(u_n\right)$ không phải là cấp số nhân

Chọn B

Áp dụng công thức số hạng tổng quát cấp số nhân ta có:

$\begin{array}{l}{u}_n=u_1{q}^{n-1}\Rightarrow u_7=u_1.q^6\\ \Rightarrow q^6=-32:\frac{-1}{2}=64\\ \Rightarrow \left[\begin{array}{l}q=2\\ q=-2\end{array}\right.\end{array}$

Chọn C

Ta có : $u_2=u_1.q=4.\left(-4\right)=-16;$

$\begin{array}{l}{\text{ u}}_3=u_2.q\\ =-16.\left(-4\right)=64;\\ {\text{u}}_4=u_3.q\\ =64.\left(-4\right)=-256\end{array}$

Số hạng tổng quát:  $u_n= 4. {( - 4)}^{n - 1}$

Chọn B

Ta có

$\begin{array}{l}{u}_n=u_1.q^{n-1}\\ \Rightarrow \frac{1}{{10}^{103}}=-1.{\left(-\frac{1}{10}\right)}^{n-1}=\frac{{(-1)}^n}{{10}^{n-1}}\end{array}$.

$\Rightarrow n-1=103\Rightarrow n=104$

Chọn B

Ta có: $\frac{u_{n+1}}{u_n}=\frac{3^{\frac{n+1}{2}+1}}{3^{\frac{n}{2}+1}}= 3^{\frac{1}{2}}=\sqrt{3},\forall n\in N^{*}$

Dãy số là cấp số nhân với $u_1=3\sqrt{3};q=\sqrt{3}$

Chọn C

Ta có $u_2;u_4;u_6;\dots ;u_{20}$ lập thành cấp số nhân số hạng đầu $u_2=9;q=3$ và có 10 số hạng nên 

$S=u_2.\frac{1-3^{10}}{1-3}=9.\frac{3^{10}-1}{2}=\frac{9}{2}(3^{10}-1)$

Chọn D

Ta có :

$\begin{array}{l}{u}_n=19683\\ \iff 3^{\frac{n}{2}+1}=3^9\\ \iff \frac{n}{2}+1=9\\ \iff n=16\end{array}$ 

Vậy số 19683 là số hạng thứ 16 của cấp số.

Chọn D.

Gọi cấp số nhân đó là (u_n), $n=\overline{\mathrm{1,7}}$. Theo đề bài ta có :

$$\begin{gathered} \left\{\begin{array}{c}{u}_4=6\\ u_7=243u_2\end{array}\right.\iff \left\{\begin{array}{c}{u}_1.q^3=6\\ u_1.q^6=243u_1.q\end{array}\right. \\ \iff \left\{\begin{array}{l}{u}_1. 3^3= 6\\ q^5= 243\end{array}\right.\iff \left\{\begin{array}{c}{u}_1=\frac{2}{9}\\ q=3\end{array}\right. \end{gathered}$$

Do đó các số hạng còn lại của cấp số nhân là

$\begin{array}{l}{u}_1=\frac{2}{9};u_2=\frac{2}{3};u_3=2;\\ u_5=18;u_6=54;u_7=162\end{array}$

Chọn C

Ta có: $u_2=u_1.q\iff \frac{1}{4}=u_1.q$ ; $u_5=u_1.q^4\iff 16=u_1.q^4$

Suy ra:

$\begin{array}{l}\frac{u_5}{u_2}=\frac{u_1{q}^4}{u_{1}q}=q^3=64\\ \iff q=4\end{array}$

Từ đó: $u_1=\frac{1}{16}.$ 

Chọn C

Gọi q là công bội của cấp số. Khi đó ta có

$\left\{\begin{array}{c}{u}_1+u_2+u_3+u_4+u_5=11\\ u_1+u_5=\frac{82}{11}\end{array}\right.$

$\begin{array}{l}\iff \left\{\begin{array}{l}{u}_2+u_3+u_4=\frac{39}{11}\\ u_1+u_5=\frac{82}{11}\end{array}\right.\\ \iff \left\{\begin{array}{l}{u}_1\left(q+q^2+q^3\right)=\frac{39}{11}\\ u_1\left(1+q^4\right)=\frac{82}{11}\end{array}\right.\end{array}$

Suy ra: 

$\begin{array}{l}\frac{q^4+1}{q^3+q^2+q}=\frac{82}{39}\\ \iff 39q^4-82q^3-82q^2-82q+39=0\end{array}$

$\begin{array}{l}\iff (3q-1)(q-3)(13q^2+16q+13)=0\\ \iff q=\frac{1}{3},q=3\end{array}$

$\begin{array}{l}q=\frac{1}{3}\Rightarrow u_1=\frac{81}{11}\\ \Rightarrow u_n=\frac{81}{11}.\frac{1}{3^{n-1}}\end{array}$

$\begin{array}{l}q=3\Rightarrow u_1=\frac{1}{11}\\ \Rightarrow u_n=\frac{3^{n-1}}{11}\end{array}$

Chọn C

Gọi q là công bội của cấp số. Khi đó ta có

$$\begin{gathered} \left\{\begin{array}{l}{u}_1+u_2+\hspace{0.17em}{u}_3+\hspace{0.17em}{u}_4+\hspace{0.17em}{u}_5= 11\\ u_1 +\hspace{0.17em}{u}_5= \frac{82}{11}\end{array}\right.\iff \left\{\begin{array}{l}{u}_2+\hspace{0.17em}{u}_3+\hspace{0.17em}{u}_4= \frac{39}{11}\\ u_1 +\hspace{0.17em}{u}_5= \frac{82}{11}\end{array}\right. \\ \iff \left\{\begin{array}{l}{u}_1(q +\hspace{0.17em}{q}^2+\hspace{0.17em}{q}^3) = \frac{39}{11} \left(1\right)\hspace{0.17em}\\ u_1( 1+\hspace{0.17em}{q}^4) = \frac{82}{11} \left(2\right)\end{array}\right. \end{gathered}$$

Lấy (2) chia (1) ta được:

$$\begin{gathered} \frac{1 +\hspace{0.17em}{q}^4}{q +\hspace{0.17em}{q}^2+\hspace{0.17em}{q}^3}= \frac{82}{39}\iff 39 +\hspace{0.17em}39q^4= 82q +\hspace{0.17em}82q^2+\hspace{0.17em}82q^3 \\ \iff 39q^4- 82q^3-\hspace{0.17em}82q^2+\hspace{0.17em}82q- 39= 0 \\ \iff q = 3; q = \frac{1}{3} \end{gathered}$$

Ta có $S_{2011}=u_1\frac{q^{2011}-1}{q-1}$

+ Với $q=\frac{1}{3}\Rightarrow u_1= \frac{81}{11}\Rightarrow S_{2011}=\frac{243}{22}\left(1-\frac{1}{3^{2011}}\right)$

+ Với $q=3\Rightarrow u_1= \frac{1}{11}\Rightarrow S_{2011}=\frac{1}{22}\left(3^{2011}-1\right)$

Chọn B

$$\begin{gathered} a^2=\left(-\frac{1}{5}\right).\left(-\frac{1}{125}\right)=\frac{1}{625} \\ \iff a=\pm \frac{1}{25} \end{gathered}$$

Chọn D

$\begin{array}{l}{\text{\hspace{0.33em}S}}_n=2^2+\frac{1}{2^2}+2+2^4+\frac{1}{2^4}+2+\mathrm{...}+2^{2n}+\frac{1}{2^{2n}}+2\\ =\left(2^2+2^4+\mathrm{...}+2^{2n}\right)+\left(\frac{1}{2^2}+\frac{1}{2^4}+\mathrm{...}+\frac{1}{2^{2n}}\right)+2n\\ =4.\frac{1-4^n}{1-4}+\frac{1}{4}\frac{1-\frac{1}{4^n}}{1-\frac{1}{4}}+2n\\ = \frac{4}{3}. (\hspace{0.17em}{4}^n-1)+\hspace{0.17em}\frac{1}{3}.\frac{4^n-1}{4^n}+\hspace{0.17em}2n \\ =\frac{4^n-1}{3}\left(4-\frac{1}{4^n}\right)+2n.\end{array}$

Chọn C

Kiểm tra các đáp án

A. Dãy số đã cho là cấp số nhân với công bội q = -2 .

B. Dãy số đã cho là cấp số nhân với công bội q= 0 .

C.

$\begin{array}{l}\frac{u_{n+1}}{u_n}=\frac{(n+\text{}1){.6}^{n+\text{}1+1}}{n{.6}^{n+1}}\\ =\frac{6\left(n+1\right)}{n},\forall n\in {\mathbb{N}}^{*}\end{array}$ , không phải là hằng số.

Vậy $\left(u_n\right):u_n=n{.6}^{n+1}$ không phải là cấp số nhân.

D. $\frac{v_{n+1}}{v_n}=\frac{{\left(-1\right)}^{n+1}{3}^{2\left(n+1\right)} }{{\left(-1\right)}^n{3}^{2n}}=\frac{{\left(-1\right)}^{n+ 1}{3}^{2n + 2} }{{\left(-1\right)}^n{3}^{2n}} =-\mathrm{9,}\forall n\in {\mathbb{N}}^{*}$ . Vậy $\left(v_n\right):v_n={\left(-1\right)}^n{.3}^{2n}$ là một cấp số nhân.

Chọn A

Ta có: $\frac{u_{n+1}}{u_n}=\frac{{4.3}^{n+1}}{{4.3}^n}=3$ không phụ thuộc vào n suy ra dãy $\left(u_n\right)$ là một cấp số nhân với công bội q = 3.

Chọn C

$u_n=u_1.q^{n-1}\Rightarrow 192=3.{\left(-2\right)}^{n-1}$

$\begin{array}{l}\Rightarrow {\left(-2\right)}^{n-1}=64={(-2)}^6\\ \Rightarrow n-1=6\Rightarrow n=7\end{array}$

Chọn D

Gọi q là công bội của cấp số. Theo giả thiết ta có

$\begin{array}{l}\left\{\begin{array}{l}{u}_1{q}^3=\frac{2}{27}\\ u_1{q}^2=243.u_1{q}^7\end{array}\right.\\ \iff \left\{\begin{array}{l}{u}_1{q}^3=\frac{2}{27}\\ q^5=\frac{1}{243}\end{array}\right.\iff \left\{\begin{array}{l}q=\frac{1}{3}\\ u_1=2\end{array}\right.\end{array}$

Ta có:

$\begin{array}{l}{u}_n=\frac{2}{3^{n-1}}\Rightarrow u_n=\frac{2}{6561}\\ \iff 3^{n-1}=6561=3^8\Rightarrow n=9\end{array}$

Vậy $\frac{2}{6561}$ là số hạng thứ 9 của cấp số.

Chọn C

Ba số: $2x-1;x;2x+1$ theo thứ tự lập thành cấp số nhân

$$\begin{gathered} \iff \left(2x-1\right)\left(2x+1\right)=x^2 \\ \iff 4x^2-1=x^2 \\ \iff 3x^2=1 \\ \iff x=\pm \frac{1}{\sqrt{3}}. \end{gathered}$$

Chọn A

Gọi q là công bội của cấp số nhân (u_n)

Ta có: u₁ = 3; u₂ = 3q; u₃ = 3q²

 $\begin{array}{l}\Rightarrow 15u_1-4u_2+u_3=15.3-4.3q+3q^2\\ =45-12q+3q^2\\ =3{\left(q-2\right)}^2+33\ge 33 \forall q.\end{array}$

Suy ra $15u_1-4u_2+u_3$  đạt GTNN khi q = 2 .

Khi đó  $u_{13}=u_1{q}^{12}= 3.2^{12}=12288.$ 

Chọn A

$S_n=\frac{8}{9}\left(9+99+999+\underset{nso9}{\underbrace{\mathrm{99...9}}}\right)$

$$\begin{gathered} =\frac{8}{9}\left(10-1+{10}^2-1+{10}^3-1+\mathrm{...}+{10}^n-1\right) \\ \begin{array}{l}=\frac{8}{9}\left[\left(10+{10}^2+{10}^3+\mathrm{...}+{10}^n\right)-n\right]\\ =\frac{8}{9}\left(10.\frac{1-{10}^n}{1-10}-n\right)\\ =\frac{80\left({10}^n-1\right)}{81}-\frac{8}{9}n.\\ \end{array} \end{gathered}$$

Chọn D

+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt $x_1,x_2,x_3$ lập thành một cấp số nhân.

Theo định lý Vi-ét, ta có $x_1.x_2.x_3=8$

Theo tính chất của cấp số nhân, ta có $x_1{x}_3=x_2^2$. Suy ra ta có $x_2^3=8\iff x_2=2.$

Với nghiệm x=2 thay vào phương trình đã cho ta có

$$\begin{gathered} 2^3- 7.2^2+ 2.(m^2+ 6m).2 - 8 = 0 \\ \iff 4m^2+\hspace{0.17em} 24m - 28 = 0 \end{gathered}$$

$m^2+6m-7=0\iff \left[\begin{array}{l}m=1\\ m=-7\end{array}\right.$ 

+ Điều kiện đủ: Với m= 1 hoặc m = -7 thì $m^2+6m=7$ nên ta có phương trình: $x^3-7x^2+14x-8=0.$

Giải phương trình này, ta được các nghiệm là 1,2,4 

Hiển nhiên ba nghiệm này lập thành một cấp số nhân với công bôị q=2

Vậy m= 1 và m=  -7  là các giá trị cần tìm.

Chọn B

Do 3 số a, b, c theo thứ tự lập thành cấp số nhân nên ta có :

$ac=b^2\Rightarrow \frac{1}{b^2}=\frac{1}{ac}$

Chọn B

Ta có 8= 2. 4 nên công bội q = 4

Do đó, x = 2.q² = 2. 4² =  32

Chọn B

Ta có cấp số nhân (u_n) có:

$\begin{array}{l}\left\{\begin{array}{l}{u}_k=16\\ u_{k+1}=36\end{array}\right.\\ \Rightarrow q=\frac{u_{k+1}}{u_k}=\frac{9}{4}\\ \Rightarrow u_{k+2}=u_{k+1}q=36.\frac{9}{4}=81\end{array}$

Chọn C

Từ giả thiết suy ra $3S=3+{2.3}^2+{3.3}^3+\mathrm{...}+{11.3}^{11}$. Do đó 

$\begin{array}{l}-2S=S-3S\\ =1+3+3^2+\mathrm{...}+3^{10}-{11.3}^{11}\\ =1.\frac{1-3^{11}}{1-3}-{11.3}^{11}\\ =-\frac{1}{2}-\frac{{21.3}^{11}}{2}\\ \Rightarrow S=\frac{1}{4}+\frac{21}{4}{.3}^{11}.\end{array}$

vì 

$\begin{array}{l}S=\frac{1}{4}+\frac{{21.3}^{11}}{4}=a+\frac{{21.3}^b}{4}\\ \Rightarrow a=\frac{1}{4},b=11\\ \Rightarrow P=\frac{1}{4}+\frac{11}{4}=3.\end{array}$

Chọn A

Theo giả thiết ta có :

$\begin{array}{l}\left\{\begin{array}{l}y=xq;z=x{q}^2\\ x+3z=2\left(2y\right)\end{array}\right.\\ \Rightarrow x+3x{q}^2=4xq\\ \Rightarrow x\left(3q^2-4q+1\right)=0\\ \iff \left[\begin{array}{l}x=0\\ 3q^2-4q+1=0\end{array}\right..\end{array}$

Nếu $x=0\Rightarrow y=z=0\Rightarrow$ công sai của cấp số cộng: x ; 2y ;  3z bằng 0 (vô lí).

nếu

$\begin{array}{l}3q^2-4q+1=0\\ \iff \left[\begin{array}{l}q=1\\ q=\frac{1}{3}\end{array}\right.\iff q=\frac{1}{3}\left(q\cancel{=}1\right).\end{array}$

Chọn C

*Theo tính chất của cấp số cộng , ta có x+  z = 2y.

Kết hợp với giả thiết, x+ y + z = 21, ta suy ra  3y = 21 nên y =  7.

* Gọi d là công sai của cấp số cộng thì $x=y-d=7-d$ và $z=y+d=7+d$.

Sau khi thêm các số 2 ; 3 ; 9 vào ba số x ; y ; z ta được ba số là x+ 2 ; y + 3 ; z + 9 hay

9- d ;  10 ; 16+ d.

 * Theo tính chất của cấp số nhân, ta có

$\begin{array}{l}\left(9-d\right)\left(16+d\right)={10}^2\\ \iff d^2+7d-44=0\end{array}$

Giải phương trình ta được d= -11 hoặc d= 4.

   Với d = -11 ; cấp số cộng 18 ; 7 ; - 4. Lúc này F = 389.

   Với d= 4, cấp số cộng 3 ; 7 ; 11. Lúc này F = 179.

Chọn A

+ Ba số $x+6y\mathrm{,5}x+2y\mathrm{,8}x+y$ lập thành cấp số cộng nên

$\begin{array}{l}\left(x+6y\right)+\left(8x+y\right)=2\left(5x+2y\right)\\ \iff 9x+\text{}7y=10x+\text{\hspace{0.17em}}4y\\ \iff x=3y\end{array}$

+ Ba số $x+\frac{5}{3},y-\mathrm{1,2}x-3y$ lập thành cấp số nhân nên $\left(x+\frac{5}{3}\right)\left(2x-3y\right)={\left(y-1\right)}^2$.

Thay x= 3y vào ta được :

$\begin{array}{l}\left(3y+\frac{5}{3}\right)\left(2.3y-3y\right)={\left(y-1\right)}^2\\ \iff \left(3y+\frac{5}{3}\right).3y=y^2-2y+\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}1\\ \iff 9y^2+\text{}5y-y^2+\text{}2y-1=0\end{array}$

$\iff 8y^2+7y-1=0\iff y=-1$ hoặc $y=\frac{1}{8}$ .

Với y= -1 thì x= - 3; với $y=\frac{1}{8}$ thì $x=\frac{3}{8}$.

Chọn B

Giả sử ba số hạng a,  b, c lập thành cấp số cộng thỏa yêu cầu, khi đó b, a, c theo thứ tự đó lập thành cấp số nhân  công bội q. Ta có

$\begin{array}{l}\left\{\begin{array}{l}a+c=2b\\ a=bq;c=b{q}^2\end{array}\right.\\ \Rightarrow bq+b{q}^2=2b\iff b. (q + q^2- 2 ) = 0\\ \iff \left[\begin{array}{l}b=0\\ q^2+q-2=0\end{array}\right..\end{array}$ 

     Nếu  $b=0\Rightarrow a=b=c=0$ nên a, b, c là cấp số cộng công sai d= 0 (vô lí).

     Nếu $q^2+q-2=0\iff q=1$ hoặc  q= -2. Nếu $q=1\Rightarrow a=b=c$ (vô lí), do đó q = -2.

Đáp án đúng: A

*Lời giải

Diện tích bề mặt của mỗi tầng (kể từ 1) lập thành một cấp số nhân có công bội $q=\frac{1}{2}$ và$u_1=\frac{12288}{2}=6144.$

Khi đó diện tích mặt trên cùng là : $u_{11}=u_1{q}^{10}=\frac{6144}{2^{10}}=6$ 

*Phương pháp giải

- xét từng ý, vận dụng tính chất của cấp số nhân: số hạng thứ nhất và công bội q

- khi đó sẽ tính được diện tích mặt trên cùng ( tầng thứ 11 ) hay u11 = ? 

*Lý thuyết cần nắm và các dạng bài toán về cấp số nhân:

- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.

Số q được gọi là công bội của cấp số nhân.

- Nếu (u_n) là cấp số nhân với công bội q, ta có công thức truy hồi:

u_{n + 1} = u_n. q với $n\in \mathbb{N}*$.

- Đặc biệt

Khi q = 0, cấp số nhân có dạng u₁, 0, 0, …., 0,…..

Khi q = 1, cấp số nhân có dạng u₁, u₁, u₁, …., u₁,…

Khi u₁ = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, 0, 0,…, 0..

Số hạng tổng quát.

- Định lí: Nếu cấp số nhân có số hạng đầu u₁ và công bội q thì số hạng tổng quát u_n được xác định bởi công thức: u_n = u₁.q^{n - 1} với n ≥ 2.

Tính chất các số hạng của cấp số nhân

- Định lí: Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:

$u_k^2=u_{k-1}.u_{k+\text{}1};k\ge 2$

( hay $\left|u_k\right|=\sqrt{u_{k-1}.u_{k+\text{}1}}$).

Tổng n số hạng đầu của một cấp số nhân.

- Định lí: Cho cấp số nhân (u_n) với công bội q ≠ 1. Đặt S_n = u₁ + u₂ + …+ u_n .

Khi đó: $S_n=\frac{u_1(1-q^n)}{1-q}$.

- Chú ý: Nếu q = 1 thì cấp số nhân là u₁, u₁, u₁,….u₁,….Khi đó, S_n = n.u₁.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Cấp số nhân (mới + Bài Tập) – Toán 11

Toán 11 Bài 3  giải SGK (Cánh diều): Cấp số nhân

TOP 40 câu Trắc nghiệm Cấp số nhân (có đáp án) – Toán 11

Chọn D

Ta có:  $u_{n +1}= 4^{n +1}+ n +1$

Chọn D 

Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:

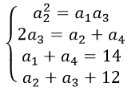
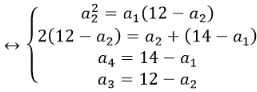
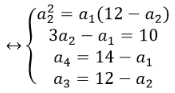
Từ $3a_2- a_1= 10 \Rightarrow a_1= 3a_2- 10$ thay vào (1) ta được: 

$$\begin{gathered} a_2^2= (\hspace{0.17em}3a_2-10). (12- a_2) \\ \iff a_2^2= 36a_2- 3a_2^2- 120+\hspace{0.17em}10a_2 \\ \iff 4a_2^2- 46a_2+\hspace{0.17em}120 = 0 \\ \Rightarrow a_2= 4; a_2= \frac{15}{2} \hspace{0.17em}\left(loại\right) \end{gathered}$$

Từ đó, ta tìm được 4 số cần tìm là:   a1=2, a2=4, a3=8 và a4=12

Chọn D

Chọn A

Số tiền là 1000000. (1+0,0065)24≈ 1168236,3