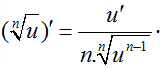50 câu hỏi trắc nghiệm thuộc 30 Đề thi thử thpt quốc gia môn Toán hay nhất có lời giải chi tiết (Đề 3)

Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại B, AB=a, $∠ A B C = 45 °$ cạnh bên SA vuông góc với mặt phẳng đáy một góc $60 °$ . Tính thể tích V của khối chóp S.ABC

A. $V = \frac{a^{3} \sqrt{3}}{9}$

B. $V = \frac{a^{3} \sqrt{3}}{6}$

C. $V = \frac{a^{3}}{4 \sqrt{3}}$

D. $V = \frac{a^{3} \sqrt{3}}{18}$

Xem đáp án

Câu 2:

Trong các hàm số sau, hàm số đồng biến trên R là

A. $y = x^{4} + 3 x^{2} - 1$

B. $y = x^{3} - 3 x^{2} + 6 x + 2$

C. $y = x^{4} - 3 x^{2} - 5$

D. $y = \frac{3 - 2 x}{x + 1}$

Xem đáp án

Câu 3:

Cho hàm số phù hợp với bảng biến thiên sau. Mệnh đề nào đúng?

A. Hàm số đồng biến trên khoảng $(- \infty; - 1) \cup (1; + \infty)$ và nghịch biến trên $(- 1; 0) \cup (0; 1))$

B. Hàm số đồng biến trên hai khoảng $(- \infty; - 1); (11; + \infty)$ và nghịch biến trên $(- 1; 11)$

C. Hàm số đồng biến trên hai khoảng $(- \infty; - 1); (1; + \infty)$ và nghịch biến trên khoảng $(- 1; 1)$

D. Hàm số đồng biến trên hai khoảng $(- \infty; - 1); (1; + \infty)$ và nghịch biến trên hai khoảng $(- 1; 0); (0; 1)$

Xem đáp án

Đáp án D

Câu 4:

12/07/2024

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AB=2a, $A A' = a \sqrt{3}$ . Tính thể tích khối lăng trụ ABC.A’B’C’

A. $3 a^{3}$

B. $a^{3}$

C. $\frac{a^{3}}{4}$

D. $\frac{3 a^{3}}{4}$

Xem đáp án

Câu 5:

Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và $∠ A B C = 120 °$ . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC

A. $\frac{a \sqrt{2}}{5}$

B. $a \sqrt{2}$

C. $a \sqrt{5}$

D. $\frac{a \sqrt{2}}{4}$

Xem đáp án

Dựng tam giác đều IAB (I và C cùng phía bờ AB). Ta có $∠ I B C = 120 ° - 60 ° = 60 °$ và IB=BC nên DIBC đều, IA=IB=IC=a

Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.

Gọi M là trung điểm của SA.

Câu 6:

21/07/2024

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=AA’=a, AC=2a. Khoảng cách từ điểm D đến mặt phẳng (ACD’) là

A. $\frac{a \sqrt{3}}{3}$

B. $\frac{a \sqrt{5}}{5}$

C. $\frac{a \sqrt{10}}{5}$

D. $\frac{a \sqrt{21}}{7}$

Xem đáp án

Câu 7:

12/07/2024

Nếu cạnh của một hình lập phương tăng lên gấp 3 lần thì thể tích của hình lập phương đó tăng lên bao nhiêu lần?

A. 27

B. 9

C. 6

D. 4

Xem đáp án

Câu 8:

Cho hình chóp S.ABCD có đáy hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN,SC) bằng

A. $45 °$

B. $30 °$

C. $90 °$

D. $60 °$

Xem đáp án

Đáp án C

MN là đường trung bình của tam giác DAS nên MN//SA.

Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên

Câu 9:

Cho hình trụ có diện tích toàn phần là 8ᴨ và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ?

A. $\frac{4 π}{9}$

B. $\frac{π \sqrt{6}}{9}$

C. $\frac{16 π \sqrt{3}}{9}$

D. $\frac{π \sqrt{6}}{12}$

Xem đáp án

Đáp án C

Gọi bán kính đường tròn đáy là r. Vì thiết diện cắt bởi mặt phẳng qua trục là hình vuông nên chiều cao hình trụ là 2r.

Câu 10:

Mệnh đề nào sau đây là đúng?

A. Hàm số y=f(x) đồng biến trên khoảng (a;b) khi và chỉ khi $f' (x) \geq 0 \forall x \in (a; b)$

B. Nếu $f' (x) \geq 0 \forall x \in (a; b)$ thì hàm số y=f(x) đồng biến trên (a;b)

C. Hàm số y=f(x) đồng biến trên khoảng (a;b) khi và chỉ khi $f' (x) > 0 \forall x \in (a; b)$

D. Nếu $f' (x) > 0 \forall x \in (a; b)$ thì hàm số y=f(x) đồng biến trên khoảng (a;b)

Xem đáp án

Câu 11:

Cho hình hộp đứng $A B C D . A_{1} B_{1} C_{1} D_{1}$ có đáy ABCD là hình vuông cạnh 2a, đường thẳng $D B_{1}$ tạo với mặt phẳng (BCC1B1) góc $30 °$ . Tính thể tích khối hộp $A B C D . A_{1} B_{1} C_{1} D_{1}$

A. $a^{3} \sqrt{3}$

B. $\frac{a^{3} \sqrt{2}}{3}$

C. $8 a^{3} \sqrt{2}$

D. $a^{3}$

Xem đáp án

Câu 12:

Đồ thị trong hình bên là đồ thị của hàm số nào trong các hàm số sau

A. $y = x^{3} - 3 x + 1$

B. $y = x^{4} - 2 x^{2} + 1$

C. $y = - x^{3} + 3 x - 1$

D. $y = 2 x^{3} - 3 x^{2} + 1$

Xem đáp án

Đáp án A

Câu 13:

Hàm số mũ và hàm số lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải

Trong các đường thẳng sau, đường thẳng nào là đường thẳng đi qua điểm A(3;0) và tiếp xúc với đồ thị hàm số y=-1/3 x^3 +3x ?

A. $y = \frac{2}{5} x + \frac{7}{5}$

B. $y = - \frac{3}{4} x + \frac{9}{4}$

C. $y = 6 x - 18$

D. $y = - 6 x + 18$

Xem đáp án

Câu 14:

19/11/2024

Với a là số thực dương bất kì, mệnh đề nào dưới đây là đúng?

A. $\ln 3 a = \ln 3 + \ln a$

B. $\ln \frac{a}{3} = \frac{1}{3} \ln a$

C. $\ln a^{5} = \frac{1}{5} \ln a$

D. $\ln (3 + a) = \ln 3 + \ln a$

Xem đáp án

Đáp án đúng: A

*Lời giải:

Tương tự như hàm số Logarit: Ta có

- ln3a = ln3 + lina nên đáp án A đúng

- ln(a/3) = lna - ln3 nên đáp án B sai

- lna⁵ = 5lna

*Phương pháp giải:

- Áp dụng logarit của một tích: Loga(b1. b2) = logab1 + logab2

- Áp dụng logarit của một lũy thừa: Logab = b loga

- Áp dụng logarit của một thương: Log b1/b2 = logb1 - logb2

* Lý thuyết cần nắm và dạng toán về hàm số logarit và hàm số mũ:

HÀM SỐ LOGARIT:

Định nghĩa logarit

Cho hai số dương a; b với a ≠ 1. Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là logab.

$α = \log_{a} b \Leftrightarrow a^{α} = b$

– Chú ý: Không có logarit của số âm và số 0.

Tính chất của logarit

Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:

loga1 = 0; logaa = 1

$a^{\log_{a} b} = b; \log_{a} (a^{α}) = α$

Quy tắc tính logarit

Logarit của một tích

– Định lí 1. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:

$\log_{a} (b_{1} . b {}_{2}) = \log_{a} b_{1} + \log_{a} b {}_{2}$

Logarit của một tích bằng tổng các logarit.

– Chú ý:

Định lí 1 có thể mở rộng cho tích n số dương:

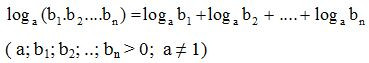
Logarit của một thương

– Định lí 2. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:

$\log_{a} \frac{b_{1}}{b_{2}} = \log_{a} b_{1} - \log_{a} b {}_{2}$

Logarit của một thương bằng hiệu các logarit.

Đặc biệt: $\log_{a} \frac{1}{b} = - \log_{a} b$ ( a > 0; b > 0; a ≠ 1)

Logarit của một lũy thừa

– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:

$\log_{a} b^{α} = α \log_{a} b$

Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.

– Đặc biệt: $\log_{a} \sqrt[n]{b} = \frac{1}{n} \log_{a} b$

Đổi cơ số logarit

– Định lí 4. Cho ba số dương a; b; c với a ≠ 1; c ≠ 1, ta có:

$\log_{a} b = \frac{\log_{c} b}{\log_{c} a}$

– Đặc biệt:

$\begin{array}{l} \log_{a} b = \frac{1}{\log_{b} a} ( b \neq 1) \\ \log_{a^{α}} b = \frac{1}{α} \log_{a} b (α \neq 0) \end{array}$

Logarit thập phân. Logarit tự nhiên

Logarit thập phân

Logarit thập phân là logarit cơ số 10.

log10b thường được viết là logb hoặc lgb.

Logarit tự nhiên

– Logarit tự nhiên là logarit cơ số e. Logeb được viết là lnb.

HÀM SỐ MŨ: y = ax, (a > 0, a ≠ 1)

Tập xác định: D = R

Tập giá trị: T = (); +∝), nghĩa là khi giải phương trình mũ mà đặt t = af(x) thì t > 0

Tính đơn điệu:

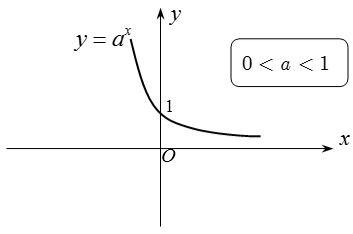
+ Khi a > 1 thì hàm số y = ax đồng biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) > g(x).

+ Khi 0 < a < 1 thì hàm số y = ax nghịch biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) < g(x).

Đạo hàm:

(ax)' = ax.ln a ⇒ (au)' = u'.au.ln a

(ex)' = ex ⇒ (eu)' = eu.u'

Các dạng bài tập Toán lớp 12 ôn thi THPT Quốc gia có lời giải

Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.

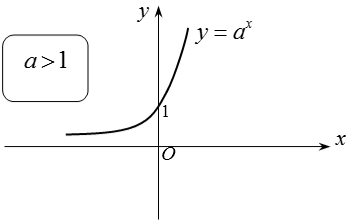
Các dạng bài tập Toán lớp 12 ôn thi THPT Quốc gia có lời giải

Xem thêm các bài viết liên quan hay, chi tiết

Toán 12 Bài 4: Hàm số mũ. Hàm số lôgarit

50 Bài tập Lôgarit Toán 12 mới nhất

Câu 15:

08/10/2024

Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng?

A. 3

B. 9

C. 6

D. 4

Xem đáp án

Đáp án đúng: B

*Phương pháp giải:

- Nắm lại kiến thức về hình lập phương: định nghĩa, tính chất, số măt, số đỉnh, số cạnh và các mặt phẳng đối xứng của hình

*Lời giải:

Hình lập phương có tất cả 9 mặt đối xứng gồm:

3 mặt phẳng chia hình lập phương thành 2 khối hộp hình chữ nhật.

6 mặt phẳng chia hình lập phương thành 2 khối lăng trụ tam giác.

*Lý thuyết nắm thêm về hình lập phương:

Công thức thể tích khối lập phương:

*) Dang bài tính thể tích khối lập phương:

+ Dạng 1:Tính thể tích hình lập phương khi biết độ dài một cạnh

* Phương pháp giải: Dựa vào đề bài cho biết độ dài của các cạnh, muốn tính thể tích hình lập phương, ta chỉ cần lấy cạnh nhân với cạnh rồi nhân với cạnh.

+ Dạng 2: Tính thể tích khối lập phương khi đã biết diện tích xung quanh hoặc diện tích toàn phần

* Phương pháp giải: Đầu tiên, ta cần phải tính diện tích 1 mặt rồi mới tìm ra được độ dài cạnh tương ứng. Sau khi đã biết được độ dài cạnh, ta áp dụng công thức thể tích như dạng 1.

+ Dạng 3: Tính độ dài cạnh khi biết được thể tích

* Phương pháp giải: Để tìm một số a chưa biết mà ta có a x a x a = V thì lúc này biết V, ta sẽ dễ dàng tính độ dài cạnh của hình lập phương.

24
Th1

Xem thêm các bài viết liên quan hay, chi tiết:

5 Đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết

Trắc nghiệm Khái niệm về khối đa diện có đáp án (Thông hiểu)

Câu 16:

Giá trị cực tiểu của hàm số y= x^3 -3x^2 -9x+2 là

A. -25

B. 3

C. 7

D. -20

Xem đáp án

Câu 17:

15/07/2024

Trong các mệnh đề sau, mệnh đề nào đúng?

A. $1 + \sin 2 x - \cos 2 x = 2 \sqrt{2} \cos x . \cos (x + \frac{π}{4})$

B. $1 + \sin 2 x - \cos 2 x = 2 \sqrt{2} \cos x (\sin x - \cos x)$

C. $1 + \sin 2 x - \cos 2 x = 2 \sqrt{2} \cos x . \cos (x - \frac{π}{4})$

D. $1 + \sin 2 x - \cos 2 x = \sqrt{2} \cos x . \cos (x - \frac{π}{4})$

Xem đáp án

Câu 18:

Trong các hàm số sau, hàm số nào nghịch biến trên R ?

A. $y = \log_{5} x$

B. $y = \log_{\frac{1}{2}} x$

C. $y = {(\frac{2}{3})}^{- x}$

D. $y = {(\frac{e}{3})}^{x}$

Xem đáp án

Câu 19:

Gọi E là tập hợp các số tự nhiên gồm 3 chữ số phân biệt từ các chữ số 1, 2, 3, 4, 5. Chọn ngẫu nhiên 2 số khác nhau từ tập hợp E. Tính xác suất để 2 số được chọn có đúng 1 số có chữ số 5

A. $\frac{7}{22}$

B. $\frac{5}{63}$

C. $\frac{144}{295}$

D. $\frac{132}{271}$

Xem đáp án

Câu 20:

$\lim_{x \to 0} \frac{\sqrt{1 - x} - 1}{x}$ bằng?

A. $- \frac{1}{2}$

B. $\frac{1}{2}$

C. $+ \infty$

D. 0

Xem đáp án

Câu 21:

Khoảng cách từ điểm M(3;-4) đến đường thẳng D: 3x-4y-1=0 bằng

A. $\frac{8}{5}$

B. $\frac{24}{5}$

C. 5

D. $\frac{7}{5}$

Xem đáp án

Câu 22:

Cho các số thực dương a,b thỏa mãn $\log a = x, \log b = y$ . Tính $l o g (a^{2} b^{3})$ ?

A. 6xy

B. $x^{3} y^{3}$

C. $x^{3} + y^{3}$

D. 2x+3y

Xem đáp án

Câu 23:

16/07/2024

Trong khoảng $(- π; π)$ , phương trình $s i n^{6} x + 3 s i n^{2} x c o s x + c o s^{6} x = 1$ có

A. 4 nghiệm

B. 1 nghiệm

C. 3 nghiệm

D. 2 nghiệm

Xem đáp án

Câu 24:

Tập xác định của hàm số $y = {(2 - x)}^{\sqrt{3}}$ là

A. R/{2}

B. R

C. (-∞;2)

D. (-∞;2]

Xem đáp án

Câu 25:

Tính thể tích V của khối nón có bán kính đáy bằng 3 và chiều cao bằng 6?

A. 18ᴨ

B. 54ᴨ

C. 108ᴨ

D. 36ᴨ

Xem đáp án

Câu 26:

Cho hàm số $y = \frac{2^{x}}{l n 2 - 2 x + 3}$ . Mệnh đề nào sau đây sai?

A. Hàm số đồng biến trên (0;+∞)

B. Hàm số có giá trị cực tiểu là $y = \frac{2}{\ln 2 + 1}$

C. Hàm số nghịch biến trên khoảng (-∞;0)

D. Hàm số đạt cực trị tại x=1

Xem đáp án

Câu 27:

Trong các số tự nhiên từ 100 đến 999 có bao nhiêu số mà các chữ số của nó tăng dần hoặc giảm dần

A. 168

B. 204

C. 216

D. 120

Xem đáp án

Đáp án B

Với ba chữ số khác nhau thuộc tập hợp {1;2;3;4;5;6;7;8;9}, ta viết được 2 số có 3 chữ số theo thứ tự tăng dần hoặc giảm dần ( $a b c$ với a>b>choặc a<b<c), có $2 . C_{9}^{3} = 168$ số

Với 2 chữ số khác nhau thuộc tập hợp {1;2;3;4;5;6;7;8;9} và 1 chữ số 0, ta viết được 1 số theo thứ tự tăng dần hoặc giảm dần ( $a b 0$ với a>b>0), có $C_{9}^{2} = 36$ số

Vậy có tất cả 168+36=204 (số).

Câu 28:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = - 2 x^{4} + 4 x^{2} + 3$ trên đoạn [0;2] lần lượt là

A. 6 và -12

B. 6 và -13

C. 5 và -13

D. 6 và -31

Xem đáp án

Câu 29:

Gía trị của m để phương trình $x^{4} - 8 x^{2} + 3 - 4 m = 0$ có 4 nghiệm thực phân biệt là:

A. $- \frac{13}{4} \leq m \leq \frac{3}{4}$

B. $- \frac{13}{4} < m < \frac{3}{4}$

C. $m \leq \frac{3}{4}$

D. $m \geq - \frac{13}{4}$

Xem đáp án

Câu 30:

Tổng các nghiệm của phương trình $l o g_{\frac{1}{3}} (x^{2} - 5 x + 7) = 0$ bằng

A. 6

B. 7

C. 13

D. 5

Xem đáp án

Đáp án D

Phương trình tương đương với $x^{2} - 5 x + 7 = 0$ , tổng các nghiệm của phương trình này là 5 (theo định lý Vi-et).

Câu 31:

Trong các mệnh đều sau, mệnh đề nào sai?

A. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng thì song song với nhau

B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau

C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau

D. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau

Xem đáp án

Đáp án D

Câu 32:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và $S A ⊥ (A B C D)$ . Biết $S A = \frac{a \sqrt{6}}{3}$ . Tính góc giữa SC và (ABCD)

A. $30 °$

B. $60 °$

C. $75 °$

D. $45 °$

Xem đáp án

Câu 33:

Phương trình $2^{x - 2} = 3^{x^{2} + 2 x - 8}$ có một nghiệm dạng $x = \log_{a} b - 4$ với a, b là các số nguyên dương thuộc khoảng (1;5) . Khi đó a+2b bằng

A. 6

B. 14

C. 9

D. 7

Xem đáp án

Câu 34:

Các đường tiệm cận của đồ thị hàm số $y = \frac{2 x + 1}{x - 1}$ là

A. x = 1; y = -2

B. x = 1; y = 2

C. x = 1; y = 0

D. x = -1; y = 2

Xem đáp án

Câu 35:

Tập nghiệm của phương trình $l o g_{2} (x^{2} - 1) = l o g_{2} (2 x)$ là

A. $S = \{\frac{1 + \sqrt{2}}{2}\}$

B. $S = \{1 + \sqrt{2}\}$

C. $S = \{1 + \sqrt{2}; 1 - \sqrt{2}\}$

D. $S = \{2; 4\}$

Xem đáp án

Câu 36:

Hàm số f(x) có đạo hàm $f ’ (x) = x^{2} (x + 1)^{3} (x + 2)$ . Số cực trị của hàm số là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C

Hàm số có 2 điểm cực trị là $x = - 1 v à x = - 2$ . Chú ý rằng $f ’ (0) = 0$ nhưng f’(x) không đổi dấu khi qua điểm $x = 0$ nên $x = 0$ không là cực trị của hàm số

Câu 37:

18/07/2024

Số hạng không chứa x trong khai triển $P (x) = {(x^{3} - \frac{1}{x^{2}})}^{5} (x \neq 0)$ là số hạng thứ

A. 3

B. 6

C. 4

D. 5

Xem đáp án

Câu 38:

Cho x, y là những số thực thỏa mãn $x^{2} - x y + y^{2} = 1$ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P = \frac{x^{4} + y^{4} + 1}{x^{2} + y^{2} + 1}$ . Giá trị của $A = M + 15 m$ là

A. $A = 17 - 2 \sqrt{6}$

B. $A = 17 - \sqrt{6}$

C. $A = 17 + \sqrt{6}$

D. $A = 17 + 2 \sqrt{6}$

Xem đáp án

Câu 39:

19/07/2024

Cho biểu thức $P = \frac{2 x y}{x^{2} + y^{2}}$ với x, y khác 0. Giá trị nhỏ nhất của P bằng

A. -2

B. 0

C. -1

D. 1

Xem đáp án

Câu 40:

Cho khai triển $(1 + 2 x)^{n} = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{n} x^{n}$ (nÎN*) và các hệ số thỏa mãn $a_{0} + \frac{a_{1}}{2} + . . . + \frac{a_{n}}{2^{n}} = 4096$ . Hệ số lớn nhất là

A. 126720

B. 1293600

C. 729

D. 924

Xem đáp án

Câu 41:

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y = \frac{x^{2}}{2} - m x + l n (x - 1)$ đồng biến trên khoảng (1;+∞) ?

A. 4

B. 1

C. 3

D. 2

Xem đáp án

Câu 42:

Hàm số $y = \frac{x - 2}{x + m - 3}$ đồng biến trên khoảng (0;+∞) khi

A. m < 1

B. m = 1

C. m ≥ 3

D. m ≠ 1

Xem đáp án

Câu 43:

Cho hàm số f(x)=ln2018-ln(x+1 / x).Tính S=f’(1)+f’(2)+f’(3)+…+f’(2017)

A. $\frac{4035}{2018}$

B. 2017

C. $\frac{2016}{2017}$

D. $\frac{2017}{2018}$

Xem đáp án

Câu 44:

Cho hai vectơ $\vec{a}$ và $\vec{b}$ khác vecto không và thảo mãn $\vec{u} = \vec{a} + \vec{b}$ vuông góc với vecto $\vec{v} = 2 \vec{a} - 3 \vec{b}$ và $\vec{m} = 5 \vec{a} - 3 \vec{b}$ vuông góc với $\vec{n} = - 2 \vec{a} + 7 \vec{b}$ . Tính góc tạo bởi hai vecto $\vec{a}$ và $\vec{b}$

A. $60 °$

B. $45 °$

C. $90 °$

D. $30 °$

Xem đáp án

Câu 45:

Tập hợp các gia trị của m để hàm số $y = \frac{1}{3} x^{3} - 6 x^{2} + (m - 2) x + 11$ có hai điểm cực trị trái dấu là

A. (-∞;38)

B. (-∞;2)

C. (-∞;2]

D. (2;38)

Xem đáp án

Câu 46:

Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ hộp ít nhất (diện tích toàn phần của lon nhỏ nhất). Bán kính đáy của vỏ lon là bao nhiêu khi muốn thể tích của lon là 314 cm^3

A. $r = \sqrt[3]{\frac{314}{4 π}}$

B. $r = 942 \sqrt[3]{2 π}$

C. $r = \sqrt[3]{\frac{314}{2 π}}$

D. $r = \sqrt[3]{\frac{314}{π}}$

Xem đáp án

Câu 47:

Tập hợp các giá trị m để hàm số $y = \frac{m x^{2} + 6 x - 2}{x + 2}$ có tiệm cận đứng là:

A. $\{\frac{7}{2}\}$

B. R

C. $R / \{- \frac{7}{2}\}$

D. $R / \{\frac{7}{2}\}$

Xem đáp án

Câu 48:

Một người gửi 50 triệu đồng vào ngân hàng với lãi suất 8,4%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập làm vốn ban đầu để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó được lĩnh số tiền không ít hơn 80 triệu đồng (cả vốn ban đầu lẫn lãi), biết rằng trong suốt thời gian gửi tiền người đó không rút tiền và lãi suất không thay đổi?

A. 4 năm

B. 7 năm

C. 5 năm

D. 6 năm

Xem đáp án

Câu 49:

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;2018] để hệ phương trình $\{\begin{cases} x - y + m = 0 \\ \sqrt{x y} + y = 1 \end{cases}$ có nghiệm?

A. 2016

B. 2018

C. 2019

D. 2017

Xem đáp án

Câu 50: