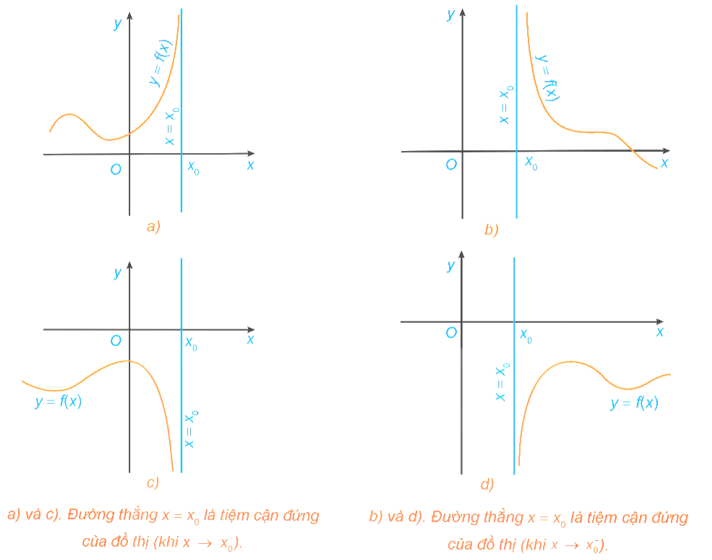50 câu hỏi trắc nghiệm thuộc 30 Đề thi thử thpt quốc gia môn Toán hay nhất có lời giải chi tiết (Đề 10)

Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Tính thể tích khối chóp S.ABC

A. $V = \frac{a^{3} \sqrt{3}}{12}$

B. $V = \frac{a^{3}}{4}$

C. $V = \frac{a^{3} \sqrt{3}}{4}$

D. $V = \frac{a^{3}}{12}$

Xem đáp án

Câu 2:

Giá trị cực tiểu của hàm số $y = - \frac{1}{3} x^{3} + x - 1$ là:

A. $- \frac{5}{3}$

B. $- \frac{1}{3}$

C. -1

D. 1

Xem đáp án

Nhận xét: Khi giải toán trắc nghiệm, thực ra không cần tính y”. Hãy nhớ rằng đồ thị hàm số bậc ba có 3 điểm cực trị và hệ số a < 0 có hình dạng như hình vẽ bên dưới.

Qua đó có thể thấy điểm cực tiểu của đồ thị hàm số là điểm cực trị bên trái, hay nói cách khác là điểm cực trị có hoành độ nhỏ hơn (nghiệm bé hơn của phương trình y’=0)

Câu 3:

Cho khối chóp có đáy hình vuông cạnh a và chiều cao bằng 2a. Thể tích của khối chóp đã cho bằng:

A. $4 a^{3}$

B. $\frac{2}{3} a^{3}$

C. $2 a^{3}$

D. $\frac{4}{3} a^{3}$

Xem đáp án

Câu 4:

21/07/2024

Số đường tiệm cận của đồ thị hàm số $y = \frac{x}{x^{2} - 1}$ nằm bên phải trục tung là

A. 2

B. 3

C. 4

D. 1

Xem đáp án

Chọn D.

Hàm số này có 2 đường tiệm cận đứng là $x = - 1, x = 1$ , đường nằm bên phái trục tung chỉ có đường $x = 1$

Câu 5:

Đường cong trong hình vẽ là đồ thị của hàm số nào trong bốn hàm số sau:

A. $y = \frac{- 2 x + 2}{x + 1}$

B. $y = \frac{- x + 2}{x + 2}$

C. $y = \frac{2 x - 2}{x + 1}$

D. $y = \frac{x - 2}{x + 1}$

Xem đáp án

Chọn A.

Nhìn vào đồ thị hàm số ta thấy:

Đồ thị hàm số có đường tiệm cận đứng $x = - 1$ loại phương án B.

Đồ thị hàm số có đường tiệm cận ngang $y = - 2$ loại phương án C,D

Câu 6:

Thể tích của khối lăng trụ có khoảng cách giữa môt đường thẳng bất kỳ của đáy này tới một đường thẳng bất kỳ của đáy kia bằng h và diện tích của đáy bằng B là:

A. $V = \frac{1}{6} B h$

B. $V = \frac{1}{3} B h$

C. $V = \frac{1}{2} B h$

D. $V = B h$

Xem đáp án

Chọn D.

Giả thiết khoảng cách giữa một đường thẳng bất kỳ của đáy này tới một đường thẳng bất kỳ của đáy kia bằng h cho ta thông tin chiều cao của lăng trụ bằng h vì 2 đáy song song với nhau. Do đó V=Bh

Câu 7:

17/07/2024

Một vật chuyển động theo quy luật $S = 10 t^{2} - \frac{1}{3} t^{3}$ , với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và S (m) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 15 giây, kể từ khi vật bắt đầu chuyển động vận tốc v (m/s) của vật đạt giá trị lớn nhất tại thời điểm t (s) bằng

A. 8 (s).

B. 20 (s).

C. 10 (s).

D. 15 (s).

Xem đáp án

Câu 8:

Cho khối tứ diện O.ABC có OA, OB, OC đôi một vuông góc và OA=a, OB=b, OC=c. Thể tích khối tứ diện O.ABC được tính theo công thức nào sau đây

A. $V = \frac{1}{6} a b c$

B. $V = \frac{1}{3} a b c$

C. $V = \frac{1}{2} a b c$

D. $V = 3 a b c$

Xem đáp án

Câu 9:

Lý thuyết Đường tiệm cận của đồ thị hàm số – Toán lớp 12 Kết nối tri thức

Khối hộp chữ nhật ABCD.A’B’C’D’ có độ dài các cạnh lần lượt là 2a, 3a và 4a. Thể tích khối hộp ABCD.A’B’C’D’ là

A. $V = 20 a^{3}$

B. $V = 24 a^{3}$

C. $V = a^{3}$

D. $V = 18 a^{3}$

Xem đáp án

Câu 10:

14/07/2024

Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = 2 x^{3} - 3 x^{2} - 12 x + 10$ trên đoạn $[- 3; 3]$ là:

A. -1

B. 18

C. -18

D. 7

Xem đáp án

Câu 11:

11/11/2024

Tọa độ tâm đối xứng của đồ thị hàm số $y = \frac{x - 2}{2 x - 1}$ là

A. $(- \frac{1}{2}; 2)$

B. $(\frac{1}{2}; \frac{1}{2})$

C. $(\frac{1}{2}; - 1)$

D. $(- \frac{1}{2}; \frac{1}{2})$

Xem đáp án

Đáp án đúng: B.

*Lời giải

Tâm đối xứng của đồ thị hàm số này là giao điểm của 2 đường tiệm cận $(\frac{1}{2}; \frac{1}{2})$

*Phương pháp giải

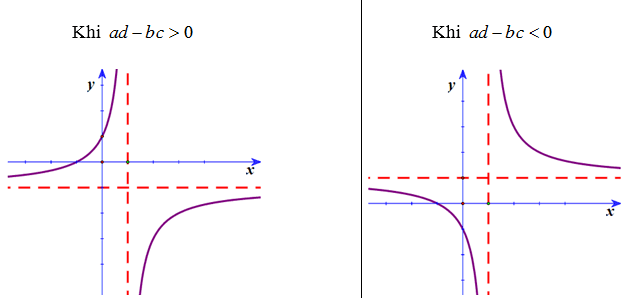
- Tâm đối xứng của đồ thị y = ax+b/cx+d là 2 đường tiệm cận của đồ thị:

*Lý thuyết cần nắm và dạng toán về đồ thị hàm số:

Các dạng đồ thị của hàm số nhất biến 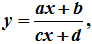(ab - bc ≠ 0)

Đường tiệm cận ngang

Đường thẳng y = y0 gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu $lim_{x \to + \infty} f (x) = y_{0}$ hoặc $lim_{x \to - \infty} f (x) = y_{0}$ .

Ví dụ 1. Tìm tiệm cận ngang của đồ thị hàm số $y = \frac{2}{x - 1}$ .

Ta có $\lim_{x \to + \infty} y = \lim_{x \to + \infty} \frac{2}{x - 1} = 0$ ; $\lim_{x \to - \infty} y = \lim_{x \to - \infty} \frac{2}{x - 1} = 0$ .

Vậy y = 0 là tiệm cận ngang của đồ thị hàm số.

Đường tiệm cận đứng

Đường thẳng x = x₀ gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

$\lim_{x \to {x_{0}}^{+}} f (x) = + \infty; \lim_{x \to {x_{0}}^{-}} f (x) = - \infty; \lim_{x \to {x_{0}}^{+}} f (x) = - \infty; \lim_{x \to {x_{0}}^{-}} f (x) = + \infty$

Ví dụ 2. Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{3 x + 6}{x - 2}$ .

Ta có $\lim_{x \to 2^{+}} y = \lim_{x \to 2^{+}} \frac{3 x + 6}{x - 2} = + \infty; \lim_{x \to 2^{-}} y = \lim_{x \to 2^{-}} \frac{3 x + 6}{x - 2} = - \infty$ .

Do đó đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

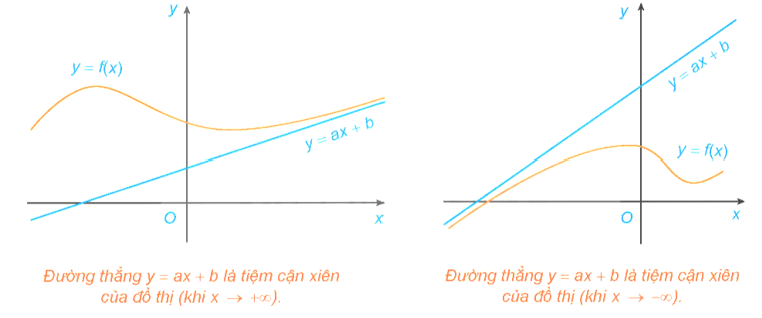
Đường tiệm cận xiên

Đường thẳng y = ax + b (a ≠ 0) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu $\lim_{x \to + \infty} [f (x) - (a x + b)] = 0$ hoặc $\lim_{x \to - \infty} [f (x) - (a x + b)] = 0$ .

Ví dụ 3.Tìm tiệm cận xiên của đồ thị hàm số $y = f (x) = 2 x + 1 - \frac{1}{x + 2}$ .

Ta có $\lim_{x \to + \infty} [f (x) - (2 x + 1)] = \lim_{x \to + \infty} (- \frac{1}{x + 2}) = 0$ ;

$\lim_{x \to - \infty} [f (x) - (2 x + 1)] = \lim_{x \to - \infty} (- \frac{1}{x + 2}) = 0$ .

Do đó y = 2x + 1 là tiệm cận xiên của đồ thị hàm số.

Chú ý:

Ta biết rằng nếu đường thẳng y = ax + b (a ≠ 0) là tiệm cận xiên của đồ thị hàm số y = f(x) thì $\lim_{x \to + \infty} [f (x) - (a x + b)] = 0$ hoặc $\lim_{x \to - \infty} [f (x) - (a x + b)] = 0$ .

Do đó $lim_{x \to + \infty} [f (x) - (a x + b)] . \frac{1}{x} = 0$ hoặc $lim_{x \to - \infty} [f (x) - (a x + b)] . \frac{1}{x} = 0$ .

Từ đây suy ra $a = \lim_{x \to + \infty} \frac{f (x)}{x}$ hoặc $a = \lim_{x \to - \infty} \frac{f (x)}{x}$ .

Khi đó, ta có $b = \lim_{x \to + \infty} [f (x) - a x]$ hoặc $b = \lim_{x \to - \infty} [f (x) - a x]$ .

Ngược lại, với a và b xác định như trên, đường thẳng y = ax + b (a ≠ 0) là một tiệm cận xiên của đồ thị hàm số y = f(x). Đặc biệt, nếu a = 0 thì đồ thị hàm số có tiệm cận ngang.

Xem thêm các bài viết liên quan hay, chi tiết:

Các dạng toán và 50 bài tập về tiệm cận của đồ thị hàm số (có đáp án 2024) – Toán 12

TOP 40 câu Trắc nghiệm Đường tiệm cận (có đáp án 2024) - Toán 12

Câu 12:

Cho hàm số $y = - x^{4} + 2 m x^{2} - 2 m + 1$ . Với gái trị nào của m thì đồ thị hàm số có 3 điểm cực trị?

A. m < 0

B. m = 0

C. m ≠ 0

D. m > 0

Xem đáp án

Câu 13:

Cho hàm số $y = \frac{3 x - 1}{- 2 + x}$ . Khẳng định nào sau đây là đúng?

A. Hàm số luôn nghịch biến trên R

B. Hàm số luôn nghịch biến trên từng khoảng xác định

C. Hàm số luôn đồng biến trên các khoảng (-∞;2) và (-2;+∞)

D. Hàm số luôn nghịch biến trên các khoảng (-∞;-2) và (-2;+∞)

Xem đáp án

Câu 14:

Cho hàm số $y = a x^{4} + b x^{2} + c (a \neq 0)$ có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên bao nhiêu khoảng?

A. 2

B. 4

C. 3

D. 1

Xem đáp án

Chọn A.

Có 2 khoảng nghịch biến của đồ thị hàm số là (-∞;-1) và (0;1)

Câu 15:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D. SA vuông góc với mặt phẳng đáy (ABCD); AB=2a; AC=CD=a. Mặt phẳng (P) đi qua CD và trọng tâm G của tam giác SAB cắt các cạnh SA, SB lần lượt tại M và N. Tính thể tích khối chóp S.CDMN theo thể tích khối chóp S.ABCD

A. $V_{S . C D M N} = \frac{14}{27} V_{S . A B C D}$

B. $V_{S . C D M N} = \frac{4}{27} V_{S . A B C D}$

C. $V_{S . C D M N} = \frac{10}{27} V_{S . A B C D}$

D. $V_{S . C D M N} = \frac{1}{2} V_{S . A B C D}$

Xem đáp án

Câu 16:

Gọi $m_{1}, m_{2}$ là các giá trị của m để hệ phương trình $\{\begin{cases} (y - 2) x - y - 1 = 0 \\ x^{2} - 2 x + y^{2} - 4 y + 5 = m^{2} \end{cases}$ có đúng 4 nghiệm nguyên. Khi đó ${m_{1}}^{2} + {m_{2}}^{2}$ bằng

A. 10

B. 9

C. 20

D. 4

Xem đáp án

Câu 17:

21/07/2024

Cho hàm số $y = f (x)$ có đồ thị như hình bên. Giá trị lớn nhất của hàm số này trên đoạn [-1;2] bằng:

A. 5

B. 2

C. 1

D. Không xác định

Xem đáp án

Câu 18:

Cho hàm số y=f(x) xác định trên R và có bảng xét dấu đạo hàm như sau:

Khi đó số điểm cực trị của đồ thị hàm số y=f(x) là

A. 3

B. 2

C. 4

D. 1

Xem đáp án

Chọn A.

Tại các điểm $x_{1}, x_{2}, x_{3}$ hàm số y=f(x) xác định và hàm số y=f’(x) không xác định hoặc bằng 0, ngoài ra hàm số y=f’(x) còn đổi dấu qua các điểm đó nên hàm số y=f(x) có 3 điểm cực trị.

Câu 19:

Hình nào dưới đây là đồ thị hàm số $y = x^{3} - 3 x^{2} + 4$ ?

A.

B.

C.

D.

Xem đáp án

Chọn C.

Hệ số a > 0, loại phương án A và D.

Đồ thị hàm số cắt trục tung tại điểm (0;4), loại phương án B.

Câu 20:

Lập phương trình tiếp tuyến với đồ thị hàm số $y = f (x)$ thỏa mãn $f^{2} (1 + 2 x) = x - f^{3} (1 - x)$ tại điểm có hoành độ $x = 1$ ?

A. $y = - \frac{1}{7} x - \frac{6}{7}$

B. $y = - \frac{1}{7} x + \frac{6}{7}$

C. $y = \frac{1}{7} x - \frac{6}{7}$

D. $y = \frac{1}{7} x + \frac{6}{7}$

Xem đáp án

Câu 21:

Cho hàm số $y = \frac{1}{3} x^{3} - \frac{1}{2} (2 m + 4) x^{2} + (m^{2} + 4 m + 3) x + 1$ (m là tham số). Tìm m để hàm số đạt cực đại tại $x_{0} = 2$

A. m = 1

B. m = -2

C. m = -1

D. m = 2

Xem đáp án

Câu 22:

Cho khối đa diện đều. Khẳng định nào sau đây sai?

A. Số đỉnh của khối lập phương bằng 8

B. Số mặt của khối tứ diện đều bằng 4

C. Khối bát diện đầu là loại {4;3}

D. Số cạnh của khối bát diện đều bằng 12

Xem đáp án

Chọn C

Khối bát diện đều là loại {3;4}

Câu 23:

Đồ thị hàm số nào sau đây có 3 điểm cực trị?

A. $y = x^{4} + 2 x^{2} - 3$

B. $y = \frac{1}{4} x^{4} - \frac{1}{3} x^{3} - \frac{1}{2} x^{2} + x + 3$

C. $y = |x^{2} - 1| - 4$

D. $y = {|x - 1|}^{3}$

Xem đáp án

Câu 24:

Cho khối chóp S.ABC có thể tích V. Nếu giữu nguyên chiều cao và tăng các đáy lên 3 lần thì thể tích khối chóp thu được là:

A. 3V

B. 6V

C. 9V

D. 12V

Xem đáp án

Chọn C.

Các đáy được tăng lên 3 lần thì diện tích tăng lên 9 lần.

$V = \frac{1}{3} S_{d} . h$ tăng lên 9 lần.

Câu 25:

19/07/2024

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. $A B = a, B C = 2 a$ cạnh bên SA vuông góc với đáy và $S A = a \sqrt{2}$ Tính thể tích khối chóp S.ABCD

A. $\frac{2 a^{3} \sqrt{3}}{3}$

B. $\frac{2 a^{3} \sqrt{2}}{3}$

C. $2 a^{3} \sqrt{2}$

D. $a^{3} \sqrt{2}$

Xem đáp án

Câu 26:

Cho hàm số y=f(x) có bảng biến thiên dưới đây. Mệnh đề nào sau đây là đúng?

A. Hàm số đạt cực tiểu tại x = 4

B. Đồ thị hàm số có đường tiệm cận ngang

C. Hàm số có $y_{C D} = 4$

D. Đồ thị hàm số có một tiệm cận đứng là đường thẳng x = 0

Xem đáp án

Câu 27:

Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 3cm. Cạnh bên tạo với đáy $60 °$ . Thể tích $(c m^{3})$ của khối chóp đó là:

A. $\frac{3 \sqrt{2}}{2}$

B. $\frac{9 \sqrt{6}}{2}$

C. $\frac{9 \sqrt{3}}{2}$

D. $\frac{3 \sqrt{6}}{2}$

Xem đáp án

Câu 28:

Hãy xác định a, b để hàm số y = 2-ax / x+b có đồ thị như hình vẽ:

A. a = 1; b = - 2

B. a = b = 2

C. a = -1; b = - 2

D. a = b = -2

Xem đáp án

Câu 29:

Cho hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

A. a > 0, b > 0, c > 0

B. a > 0, b < 0, c > 0

C. a < 0, b > 0, c > 0

D. a > 0, b < 0, c < 0

Xem đáp án

Chọn B.

Dễ thấy $\lim_{x \to \infty} y = + \infty$ nên a > 0.

Đồ thị hàm số có 3 điểm cực trị nên ab<0 => b<0

Đồ thị hàm số cắt trục tung tại điểm (0;c) có tung độ dương nên c > 0.

Câu 30:

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?

A. a > 0, b > 0, c < 0, d < 0

B. a < 0, b < 0, c > 0, d < 0

C. a > 0, b < 0, c < 0, d < 0

D. a > 0, b < 0, c > 0, d < 0

Xem đáp án

Câu 31:

17/07/2024

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc $60 °$ . Tính theo a thể tích khối chóp S.ABCD

A. $V = \frac{a^{3} \sqrt{6}}{6}$

B. $V = \frac{a^{3} \sqrt{6}}{2}$

C. $V = \frac{a^{3} \sqrt{6}}{3}$

D. $V = \frac{a^{3}}{3}$

Xem đáp án

Câu 32:

Cho lăng trụ đứng ABC.A’B’C’ có đáy là DABC vuông tại B, $A B = a$ , $\hat{B A C} = 60 °$ , $A A' = a \sqrt{3}$ . Thể tích khối lăng trụ là

A. $\frac{3 a^{3}}{2}$

B. $\frac{2 a^{3}}{3}$

C. $\frac{a^{3} \sqrt{3}}{3}$

D. $\frac{a^{3} \sqrt{3}}{9}$

Xem đáp án

Câu 33:

19/07/2024

Cho hàm số $y = \frac{x^{3}}{3} + 3 x^{2} - 2$ có đồ thị là (C) Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc $k = - 9$

A. $y + 16 = - 9 (x + 3)$

B. $y = - 9 (x + 3)$

C. $y - 16 = - 9 (x - 3)$

D. $y - 16 = - 9 (x + 3)$

Xem đáp án

Câu 34:

21/07/2024

Cho hàm số $y = f (x)$ liên tục trên D và có giá trị lớn nhất, gái trị nhỏ nhất trên D. Khi đó bất phương trình $f (x) \geq m$ có nghiệm khi và chỉ khi

A. $\underset{D}{M a x} f (x) \geq m$

B. $\underset{D}{M a x} f (x) < m$

C. $\frac{1}{2} [\underset{D}{M a x} f (x) - \underset{D}{M i n} f (x)] \geq m$

D. $\underset{D}{M i n} f (x) \leq m$

Xem đáp án

Câu 35:

Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, $\hat{B C D} = 120 °$ , $A A' = \frac{7}{2} a$ . Hình chiếu vuông góc của A’ lên mạt phẳng (ABCD) trung với giao điểm của AC và BD Tính theo a thể tích khối hộp ABCD.A’B’C’D’?

A. $3 a^{3}$

B. $\frac{4 a^{3} \sqrt{6}}{3}$

C. $2 a^{3}$

D. $\sqrt{3} a^{3}$

Xem đáp án

Câu 36:

17/07/2024

Cho tứ diện MNPQ. Gọi I;J;K lần lượt là trung điểm các cạnh MN;MP;MQ. Tỉ số thể tích $\frac{V_{M I J K}}{V_{M N P Q}}$ bằng

A. $\frac{1}{4}$

B. $\frac{1}{3}$

C. $\frac{1}{8}$

D. $\frac{1}{6}$

Xem đáp án

Câu 37:

14/07/2024

Xác định m để đồ thị hàm số $y = \frac{x - 1}{x^{2} + 2 (m - 1) x + m^{2} - 2}$ có đúng hai đường tiệm cận đứng

A. $m < \frac{3}{2}$

B. $m > - \frac{3}{2}; m \neq 1$

C. $m < - \frac{3}{2}; m \neq 1; m \neq 3$

D. $m > - \frac{3}{2}$

Xem đáp án

Câu 38:

Hàm số f(x) có đạo hàm $f ’ (x) = x^{2} (x + 2)$ . Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng (-2;+∞)

B. Hàm số nghịch biến trên các khoảng (-∞;-2) và (0;+∞)

C.Hàm số đồng biến trên các khoảng (-∞;-2) và (0;+∞)

D. Hàm số nghịch biến trên khoảng (-2;0)

Xem đáp án

Câu 39:

Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, $A A' = \frac{3 a}{2}$ . Biết rằng hình chiếu vuông góc của A’ lên (ABC) là trung điểm BC Tính thể tích V của lăng trụ đó

A. $V = \frac{2 a^{3}}{3}$

B. $V = \frac{3 a^{3}}{4 \sqrt{2}}$

C. $V = a^{3} \sqrt{\frac{3}{2}}$

D. $V = a^{3}$

Xem đáp án

Câu 40:

Cho hàm số $y = x^{4} - 2 x^{2} - 2$ có đồ thị (C) và đồ thị $(P) : y = 1 - x^{2} .$ Số giao điểm của (P) và đồ thị (C) là:

A. 1

B. 4

C. 2

D. 3

Xem đáp án

Câu 41:

19/07/2024

Cho hàm số y=f(x) có đồ thị như hình vẽ bên:

Điều kiện của m để phương trình $f (|x|) = m$ có 4 nghiệm phân biệt $x_{1}, x_{2}, x_{3}, x_{4}$ thỏa mãn $x_{1} \leq - \frac{1}{2} x_{2} < x_{3} \leq \frac{1}{2} x_{4}$ là:

A. $m \in (2; 3)$

B. $m \in [2; 3]$

C. $m \in [\frac{5}{2}; 3)$

D. $m \in [2; \frac{5}{2})$

Xem đáp án

Đồ thị hàm số có điểm uốn là trung điểm của 2 đường cực trị $I (\frac{1}{2}; \frac{5}{2})$

Số nghiệm của phương trình f(|x|)=m là số giao điểm của đồ thị hàm số y=f(|x|) và đường thẳng y=m. Để phương trình có 4 nghiệm thỏa mãn điều kiện đề bài thì $\frac{5}{2} \leq m < 3$

Câu 42:

14/07/2024

Cho hàm số $y = x^{3} - 3 x - 1$ . Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng (-∞;+∞)

B. Hàm số nghịch biến trên khoảng (-1;1)

C. Hàm số nghịch biến trên khoảng (-∞;-1)

D. Hàm số đồng biến trên khoảng (0;1)

Xem đáp án

Câu 43:

Cho hàm số y=f(x) có bảng biến thiên như sau:

Mệnh đề nào dưới đây là đúng?

A. Hàm số đạt cực đại tại x = 3

B. Hàm số đạt cực tiểu tại x = -2

C. Hàm số có $y_{C D} = 3$

D. Hàm số nghịch biến trên các khoảng (-∞;-2) và (2;+∞)

Xem đáp án

Chọn C

Câu 44:

16/07/2024

Tổng diện tích các mặt của một hình lập phương bằng 54. Thể tích của khôi lập phương là

A. 15

B. 27

C. 18

D. 21

Xem đáp án

Câu 45:

Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x,y,z (dm). Biết tỉ số hai cạnh đáy là $x : y = 1 : 3$ và thể tích của hộp bằng $18 (d m^{3})$ . Để tốn ít vật liệu nhất thì tổng $x + y + z$ bằng?

A. $\frac{26}{3}$

B. 10

C. $\frac{19}{2}$

D. 26

Xem đáp án

Câu 46:

Cho hàm số y=f(x) được xác định trên R và hàm số f=f’(x) có đồ thị như hình vẽ.

Tìm khoảng nghịch biến của hàm số $y = f (x^{2} - 3)$ ?

A. (-∞;-1) và (0;1)

B. (-1;0)

C. (-1;0)

D. (-1;1)

Xem đáp án

Câu 47:

15/07/2024

Cho hàm số $y = \sqrt{x^{2} - x - 20}$ . Mệnh đề nào dưới đây là sai?

A. Hàm số nghịch biến trên khoảng (-∞;-4)

B. Hàm số đạt cực đại tại x = 5

C. Hàm số đồng biến trên khoảng (5;+∞)

D. Hàm số không có cực trị

Xem đáp án

Câu 48:

Tìm tất cả các giá trị của m để hàm số $y = \frac{x^{3}}{3} - (m - 1) x^{2} + 2 (m - 1) x + 2$ đồng biến trên tập xác định của nó là:

A. 1 < m < 3

B. m ≥ 1

C. 1 ≤ m ≤ 3

D. m ≤ 3

Xem đáp án

Câu 49: