Tọa độ tâm đối xứng của đồ thị hàm số $y = \frac{x-2}{2x-1}$ là

Đáp án đúng: B.

*Lời giải

Tâm đối xứng của đồ thị hàm số này là giao điểm của 2 đường tiệm cận $\left(\frac{1}{2};\frac{1}{2}\right)$

*Phương pháp giải

- Tâm đối xứng của đồ thị y = ax+b/cx+d là 2 đường tiệm cận của đồ thị:

*Lý thuyết cần nắm và dạng toán về đồ thị hàm số:

Các dạng đồ thị của hàm số nhất biến 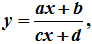(ab - bc ≠ 0)

Đường tiệm cận ngang

Đường thẳng y = y0 gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu $\underset{x\to +\infty }{lim}f\left(x\right)=y_0$ hoặc $\underset{x\to -\infty }{lim}f\left(x\right)=y_0$.

Ví dụ 1. Tìm tiệm cận ngang của đồ thị hàm số $y=\frac{2}{x-1}$ .

Ta có $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{2}{x-1}=0$ ; $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{2}{x-1}=0$ .

Vậy y = 0 là tiệm cận ngang của đồ thị hàm số.

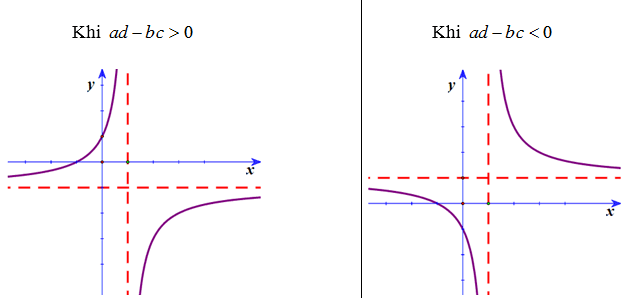
Đường tiệm cận đứng

Đường thẳng x = x₀ gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

$\underset{x\to {x_0}^{+}}{\lim }f\left(x\right)=+\infty ;\underset{x\to {x_0}^{-}}{\lim }f\left(x\right)=-\infty ;\underset{x\to {x_0}^{+}}{\lim }f\left(x\right)=-\infty ;\underset{x\to {x_0}^{-}}{\lim }f\left(x\right)=+\infty$

Ví dụ 2. Tìm tiệm cận đứng của đồ thị hàm số $y=\frac{3x+6}{x-2}$ .

Ta có $\underset{x\to 2^{+}}{\lim }y=\underset{x\to 2^{+}}{\lim }\frac{3x+6}{x-2}=+\infty ;\underset{x\to 2^{-}}{\lim }y=\underset{x\to 2^{-}}{\lim }\frac{3x+6}{x-2}=-\infty$ .

Do đó đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

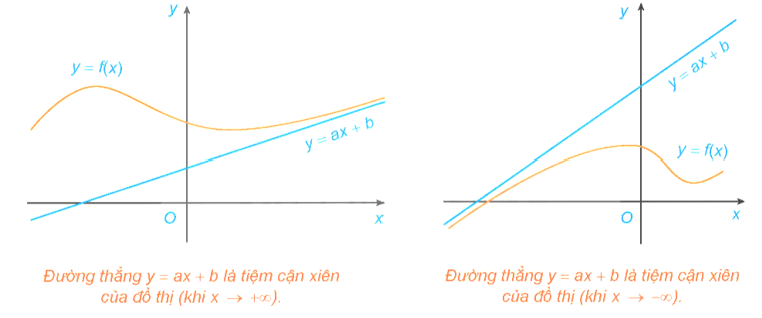
Đường tiệm cận xiên

Đường thẳng y = ax + b (a ≠ 0) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu $\underset{x\to +\infty }{\lim }\left[f\left(x\right)-\left(ax+b\right)\right]=0$ hoặc $\underset{x\to -\infty }{\lim }\left[f\left(x\right)-\left(ax+b\right)\right]=0$.

Ví dụ 3.Tìm tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=2x+1-\frac{1}{x+2}$ .

Ta có $\underset{x\to +\infty }{\lim }\left[f\left(x\right)-\left(2x+1\right)\right]=\underset{x\to +\infty }{\lim }\left(-\frac{1}{x+2}\right)=0$ ;

$\underset{x\to -\infty }{\lim }\left[f\left(x\right)-\left(2x+1\right)\right]=\underset{x\to -\infty }{\lim }\left(-\frac{1}{x+2}\right)=0$.

Do đó y = 2x + 1 là tiệm cận xiên của đồ thị hàm số.

Chú ý:

Ta biết rằng nếu đường thẳng y = ax + b (a ≠ 0) là tiệm cận xiên của đồ thị hàm số y = f(x) thì $\underset{x\to +\infty }{\lim }\left[f\left(x\right)-\left(ax+b\right)\right]=0$ hoặc $\underset{x\to -\infty }{\lim }\left[f\left(x\right)-\left(ax+b\right)\right]=0$.

Do đó $\underset{x\to +\mathrm{\infty }}{lim}[f\left(x\right)-(ax+b)].\frac{1}{x}=0$ hoặc $\underset{x\to -\mathrm{\infty }}{lim}[f\left(x\right)-(ax+b)].\frac{1}{x}=0$.

Từ đây suy ra $a=\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x}$ hoặc $a=\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x}$.

Khi đó, ta có $b=\underset{x\to +\infty }{\lim }\left[f\left(x\right)-ax\right]$ hoặc $b=\underset{x\to -\infty }{\lim }\left[f\left(x\right)-ax\right]$.

Ngược lại, với a và b xác định như trên, đường thẳng y = ax + b (a ≠ 0) là một tiệm cận xiên của đồ thị hàm số y = f(x). Đặc biệt, nếu a = 0 thì đồ thị hàm số có tiệm cận ngang.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Đường tiệm cận của đồ thị hàm số – Toán lớp 12 Kết nối tri thức 

Các dạng toán và 50 bài tập về tiệm cận của đồ thị hàm số (có đáp án 2024) – Toán 12

TOP 40 câu Trắc nghiệm Đường tiệm cận (có đáp án 2024) - Toán 12