Giải SBT Toán 10 trang 59 Tập 2 Chân trời sáng tạo

Giải SBT Toán 10 trang 59 Tập 2 Chân trời sáng tạo

Bài 3 trang 59 SBT Toán 10 Tập 2: Cho tam giác MNP có toạ độ các đỉnh là M(3; 3), N(7; 3) và P(3; 7).

a) Tìm toạ độ trung điểm E của cạnh MN.

b) Tim toạ độ trọng tâm G của tam giác MNP.

Lời giải:

a) Gọi E(x_E; y_E) là trung điểm của MN

Ta có  $\left\{\begin{array}{l}{x}_E=\frac{x_M+x_N}{2}=\frac{3+7}{2}=5\\ y_E=\frac{y_M+y_N}{2}=\frac{3+3}{2}=3\end{array}\right.$

Vậy E(5; 3).

b) Gọi G(x_G; y_G) là trọng tâm của tam giác MNP

Ta có $\left\{\begin{array}{l}{x}_G=\frac{x_M+x_N+x_P}{3}=\frac{3+7+3}{3}=\frac{13}{3}\\ y_G=\frac{y_M+y_N+y_P}{3}=\frac{3+3+7}{3}=\frac{13}{3}\end{array}\right.$

Vậy $G\left(\frac{13}{3};\frac{13}{3}\right)$ .

Bài 4 trang 59 SBT Toán 10 Tập 2: Cho tam giác ABC có toạ độ các đỉnh là A(1; 3), B(3; 1) và C(6; 4).

a) Tính độ đài ba cạnh của tam giác ABC và số đo của góc B.

b) Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC.

Lời giải:

a) + Độ dài các cạnh của tam giác ABC

 $\overrightarrow{AB}=(2;-2)\Rightarrow \left|\overrightarrow{AB}\right|=\sqrt{2^2+{(-2)}^2}=2\sqrt{2}$

Suy ra AB = $2\sqrt{2}$ .

 $\overrightarrow{BC}=(3;3)\Rightarrow \left|\overrightarrow{BC}\right|=\sqrt{3^2+3^2}=3\sqrt{2}$

Suy ra AB = $3\sqrt{2}$ .

 $\overrightarrow{AC}=(5;1)\Rightarrow \left|\overrightarrow{BC}\right|=\sqrt{5^2+1^2}=\sqrt{26}$

Suy ra AC = $\sqrt{26}$ .

+ Tính số đo góc B

Ta có  $\overrightarrow{BA}=(-2;2);\overrightarrow{BC}=(3;3)\Rightarrow \overrightarrow{BA}.\overrightarrow{BC}=-2.3+2.3=0$

 $\begin{array}{l}\overrightarrow{BA}.\overrightarrow{BC}=BA.BC.cos\left(\overrightarrow{BA},\overrightarrow{BC}\right)\\ \iff cos\left(\overrightarrow{BA},\overrightarrow{BC}\right)=\frac{\overrightarrow{BA}.\overrightarrow{BC}}{BA.BC}=\frac{-2.3+2.3}{\sqrt{{(-2)}^2+2^2}.\sqrt{3^2+3^2}}=0\end{array}$

$\Rightarrow \left(\overrightarrow{BA},\overrightarrow{BC}\right)={90}^o$

Mà  = 90^o.

b) Gọi I(x; y) là tâm đường tròn ngoại tiếp tam giác ABC:

$\overrightarrow{AI}=(x-1;y-3);\overrightarrow{BI}=(x-3;y-1);\overrightarrow{CI}=(x-6;y-4)$

Suy ra   $\left\{\begin{array}{l}A{I}^2=B{I}^2\\ A{I}^2=C{I}^2\end{array}\right.$

 $\iff \left\{\begin{array}{l}{x}^2-2x+1+y^2-6y+9=x^2-6x+9+y^2-2y+1\\ x^2-2x+1+y^2-6y+9=x^2-12x+36+y^2-8y+16\end{array}\right.$

 $\iff \left\{\begin{array}{l}4x-4y=0\\ 10x+2y=42\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{7}{2}\\ y=\frac{7}{2}\end{array}\right.$

Vậy  $I\left(\frac{7}{2};\frac{7}{2}\right)$.

Bài 5 trang 59 SBT Toán 10 Tập 2: Cho năm điểm A(2 ; 0), B(0; – 2), C(3; 3), D(– 2; – 2), E(1; – 1). Trong các điểm đã cho, hãy tìm điểm:

a) Thuộc trục hoành;

b) Thuộc trục tung;

c) Thuộc đường phân giác của góc phần tư thứ nhất.

Lời giải:

a) Điểm thuộc trục hoành là điểm có tung độ bằng 0. Do đó các điểm thuộc trục hoành là: A(2; 0).

b) Điểm thuộc trục hoành là điểm có hoành độ bằng 0. Do đó các điểm thuộc trục tung là: B(0; – 2).

c) Điểm thuộc đường phân giác của góc phần tư thứ nhất có hoành độ bằng tung độ. Do đó các điểm thuộc đường phân giác của góc phần tư thứ nhất là: C(3; 3); D(– 2; – 2).

Bài 6 trang 59 SBT Toán 10 Tập 2: Cho điểm M(4; 5). Tìm toạ độ:

a) Điểm H là hình chiếu vuông góc của điểm M trên trục Ox;

b) Điểm M’ đối xứng với M qua trục Ox;

c) Điểm K là hình chiếu vuông góc của điểm M trên trục Oy;

d) Điểm M’’ đối xứng với M qua trục Oy;

e) Điểm C đối xứng với M qua gốc O.

Lời giải:

a) Gọi H(a; 0) (a ≠ 0) là hình chiếu vuông góc của M trên trục Ox

Ta có  $\overrightarrow{OH}.\overrightarrow{MH}=0$

Mà $\overrightarrow{OH}=(a;0);\overrightarrow{MH}=(a-4;-5)$

$\overrightarrow{OH}.\overrightarrow{MH}=a.(a-4)+0.(-5)=a^2-4a=0\iff \left[\begin{array}{l}a=0\\ a=4\end{array}\right.$

Do đó chỉ có a = 4 là thỏa mãn điều kiện.

Vậy H(4; 0) là hình chiếu vuông góc của M trên trục Ox.

b) Ta có điểm M’(x’; y’) đối xứng với điểm M(x; y) qua trục Ox  $\Rightarrow \left\{\begin{array}{l}x=x\text{'}\\ y=-y\text{'}\end{array}\right.$

Vậy M’(4; – 5) là điểm đối xứng với M qua trục Ox.

c) Gọi K(0; b) (b ≠ 0) là hình chiếu vuông góc của M trên trục Oy.

Ta có  $\overrightarrow{OK}.\overrightarrow{MK}=0$

Mà $\overrightarrow{OK}=(0;b);\overrightarrow{MK}=(-4;b-5)$

$\overrightarrow{OK}.\overrightarrow{MK}=0.(-4)+b.(b-5)=b^2-5b=0\iff \left[\begin{array}{l}b=0\\ b=5\end{array}\right.$

Do đó chỉ có b = 5 là thỏa mãn điều kiện.

Vậy K(0; 5) là hình chiếu vuông góc của M trên trục Oy.

d) Ta có điểm M”(x”; y”) đối xứng với điểm M(x; y) qua trục Oy  $\Rightarrow \left\{\begin{array}{l}x=-x"\\ y=y"\end{array}\right.$

Vậy M”(– 4; 5) là điểm đối xứng với M qua trục Oy.

e) Gọi C(x; y) là điểm đối xứng với M qua gốc toạ độ O

Suy ra O là trung điểm của MC.

Ta có  $\left\{\begin{array}{l}\frac{x+4}{2}=0\\ \frac{y+5}{2}=0\end{array}\right.\iff \left\{\begin{array}{l}x=-4\\ y=-5\end{array}\right.$

Vậy C(– 4; – 5).

Bài 7 trang 59 SBT Toán 10 Tập 2: Cho ba điểm A(1; 1), B(2; 4), C(4; 4).

a) Tìm toạ độ điểm D sao cho ABCD là một hình bình hành.

b) Tìm toạ độ giao điểm hai đường chéo của hình bình hành ABCD.

Lời giải:

a)

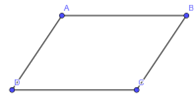
Giả sử D(x; y)

Ta có  $\overrightarrow{AB}=(1;3);\overrightarrow{DC}=(4-x;4-y)$

Để ABCD là hình bình hành thì  $\overrightarrow{AB}=\overrightarrow{DC}\iff \left\{\begin{array}{l}4-x=1\\ 4-y=3\end{array}\right.\iff \left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$

Vậy D(3; 1).

b) Gọi I là giao điểm của hai đường chéo AC và BD

Vậy I là trung điểm của AC và BD theo tính chất hình hành

Ta có  $\left\{\begin{array}{l}{x}_I=\frac{x_A+x_C}{2}=\frac{1+4}{2}=\frac{5}{2}\\ y_I=\frac{y_A+y_C}{2}=\frac{1+4}{2}=\frac{5}{2}\end{array}\right.$

Vậy $I\left(\frac{5}{2};\frac{5}{2}\right)$ .

Bài 8 trang 59 SBT Toán 10 Tập 2: Cho tam giác ABC có toạ độ các đỉnh là A(1; 1), B(7; 3), C(4; 7) và cho các điểm M(2; 3), N(3; 5).

a) Chứng minh bốn điểm A, M, N, C thẳng hàng.

b) Chứng minh trọng tâm của các tam giác ABC và MNB trùng nhau.

Lời giải:

a) Ta có $\overrightarrow{AM}=(1;2);\overrightarrow{AN}=(2;4)$  suy ra $\overrightarrow{AN}=2\overrightarrow{AM}$ . Do đó 3 điểm A, M, N thẳng hàng

Ta có $\overrightarrow{AM}=(1;2);\overrightarrow{AC}=(3;6)$  suy ra $\overrightarrow{AC}=3\overrightarrow{AM}$ . Do đó 3 điểm A, M, C thẳng hàng

Vì 3 điểm A, M, N thẳng hàng nên N thuộc đường thẳng AM; 3 điểm A, M, C thẳng hàng nên C thuộc đường thẳng AM.

Vậy 4 điểm A, M, N, C thẳng hàng.

b) Goi G(x; y) là trọng tâm tam giác ABC

Ta có  $\left\{\begin{array}{l}x=\frac{x_A+x_B+x_C}{3}=\frac{1+7+4}{3}=4\\ y=\frac{y_A+y_B+y_C}{3}=\frac{1+3+7}{3}=\frac{11}{3}\end{array}\right.$

Suy ra G  $\left(4;\frac{11}{3}\right)$.

Goi G’(x’; y’) là trọng tâm tam giác MNB

Ta có $\left\{\begin{array}{l}x\text{'}=\frac{x_M+x_N+x_B}{3}=\frac{2+3+7}{3}=4\\ y\text{'}=\frac{y_M+y_N+y_B}{3}=\frac{3+5+3}{3}=\frac{11}{3}\end{array}\right.$

Suy ra G’ $\left(4;\frac{11}{3}\right)$.

Do đó điểm G trùng G’.

Vậy trọng tâm tam giác ABC và MNB trùng nhau.

Bài 9 trang 59 SBT Toán 10 Tập 2: Cho bốn điểm M(6; – 4), N(7; 3), P(0; 4), Q(– 1; -3). Chứng minh rằng tứ giác MNPQ là hình vuông.

Lời giải:

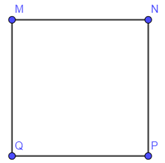
Ta có $\overrightarrow{MN}=(1;7);\overrightarrow{QP}=(1;7)\Rightarrow \overrightarrow{MN}=\overrightarrow{QP}$  nên hai véc tơ cùng phương suy ra MN song song với PQ và MN = QP (1)

Ta có $\overrightarrow{MQ}=(-7;1);\overrightarrow{NP}=(-7;1)\Rightarrow \overrightarrow{MQ}=\overrightarrow{NP}$  nên hai véc tơ cùng phương suy ra MQ song song với NP và MQ = NP (2)

Mà $\left|\overrightarrow{MN}\right|=\left|\overrightarrow{NP}\right|=\left|\overrightarrow{PQ}\right|=\left|\overrightarrow{MQ}\right|=\sqrt{50}$  vậy MN = NP = PQ = MQ (3)

Từ (1); (2); (3) suy ra tứ giác MNPQ là hình thoi (4)

Ta có  $\overrightarrow{MN}.\overrightarrow{NP}=1.(-7)+7.1=0$$\Rightarrow \overrightarrow{MN}\perp \overrightarrow{NP}$  vậy MN $\perp$  NP.

Tứ giác MNPQ là hình thoi và có 1 góc vuông nên tứ giác MNPQ là hình vuông.

Bài 10 trang 59 SBT Toán 10 Tập 2: Tính góc giữa hai vectơ $\overrightarrow{a}$  và $\overrightarrow{b}$  trong các trường hợp sau:

a) $\overrightarrow{a}=\left(1;-4\right),\overrightarrow{b}=\left(5;3\right)$

b) $\overrightarrow{a}=\left(4;3\right),\overrightarrow{b}=\left(6;0\right)$

c) $\overrightarrow{a}=\left(2;2\sqrt{3}\right),\overrightarrow{b}=\left(-3;\sqrt{3}\right)$

Lời giải:

a) Ta có  $\text{cos}\left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{1.5+(-4).3}{\sqrt{1^2+{(-4)}^2}.\sqrt{5^2+3^2}}=-\frac{7\sqrt{2}}{34}$

Vậy $\left(\overrightarrow{a},\overrightarrow{b}\right)={106}^{o}56\text{'}$ .

b) Ta có  $\text{cos}\left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{4.6+3.0}{\sqrt{4^2+3^2}.\sqrt{6^2+0^2}}=\frac{4}{5}$

Vậy $\left(\overrightarrow{a},\overrightarrow{b}\right)={36}^{o}52\text{'}$ .

c) Ta có $\text{cos}\left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{2.(-3)+2\sqrt{3}.\sqrt{3}}{\sqrt{2^2+{\left(2\sqrt{3}\right)}^2}.\sqrt{{(-3)}^2+{\sqrt{3}}^2}}=0$ .

Vậy $\left(\overrightarrow{a},\overrightarrow{b}\right)={90}^o$ .

Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo với cuộc sống hay, chi tiết khác: 

Giải SBT Toán 10 trang 58 Tập 2

Giải SBT Toán 10 trang 60 Tập 2