Giải SBT Toán 10 trang 14 Tập 2 Chân trời sáng tạo

Giải SBT Toán 10 trang 14 Tập 2 Chân trời sáng tạo

Bài 3 trang 14 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau:

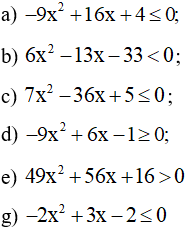
Lời giải:

a) Tam thức bậc hai f (x) = –9x² + 16x + 4 có a = – 9 < 0 và ∆ = 16² – 4.( – 9).4 = 112 > 0. Do đó f(x) có hai nghiệm phân biệt là x₁ = 2 và x₂ = $\frac{-2}{9}$

Áp dụng định lí về dấu tam thức bậc hai ta có:

$-9x^2+16x+4\le 0$ khi x ≤ $\frac{-2}{9}$ hoặc x ≥ 2.

Vậy tập nghiệm của bất phương trình là S = $\left(-\infty ;\frac{-2}{9}\right)\cup \left(2;+\infty \right)$.

b) Tam thức bậc hai f (x) = $6x^2-13x-33$ có a = 6 > 0 và ∆ = ( –13)² – 4.6.( –33) = 961 > 0. Do đó f(x) có hai nghiệm phân biệt là x₁ = $\frac{11}{3}$ và x₂ = $\frac{-3}{2}$

Áp dụng định lí về dấu tam thức bậc hai ta có:

$6x^2-13x-33$ < 0 khi $\frac{-3}{2}$ < x < $\frac{11}{3}$

Vậy tập nghiệm của bất phương trình là S = $\left(\frac{-3}{2};\frac{11}{3}\right)$.

c) Tam thức bậc hai f ( x ) = $7x^2-36x+5$ có a = 7 > 0 và 2∆ = ( –36)² – 4.7.5 = 1156 > 0. Do đó f(x) có hai nghiệm phân biệt là x₁ = $\frac{1}{7}$ và x₂ = 5

Áp dụng định lí về dấu tam thức bậc hai ta có:

$7x^2-36x+5\le 0$  khi $\frac{1}{7}$ ≤ x ≤ 5

Vậy tập nghiệm của bất phương trình là S = $\left[\frac{1}{7};5\right]$.

d) Tam thức bậc hai f ( x ) = $-9x^2+6x-1$ có a = –9 < 0 và ∆ = 6² – 4.( –9).( –1) = 0. Do đó f(x) có nghiệm x = $\frac{1}{3}$

Áp dụng định lí về dấu tam thức bậc hai ta có:

$-9x^2+6x-1\ge 0$ khi x = $\frac{1}{3}$

Vậy tập nghiệm của bất phương trình là S = $\left\{\frac{1}{3}\right\}$.

e) Tam thức bậc hai f ( x ) = $49x^2+56x+16$ = ( 7x + 4 )²

Tam thức bậc hai có nghiệm x = $\frac{-4}{7}$

Áp dụng định lí về dấu tam thức bậc hai ta có:

$49x^2+56x+16>0$  khi x ≠ $\frac{-4}{7}$

Vậy tập nghiệm của bất phương trình là S = $ℝ\backslash \left\{\frac{-4}{7}\right\}$

g)

Tam thức bậc hai f ( x ) = $-2x^2+3x-2$ có ∆ = 3² – 4. ( –2 ). ( –2 ) = –7 < 0 nên f(x) vô nghiệm.

Áp dụng định lí về dấu tam thức bậc hai ta có a = –2 < 0 nên

$-2x^2+3x-2\le 0$ với mọi x ∈ ℝ.

Vậy $-2x^2+3x-2\le 0$ với mọi x ∈ ℝ.

Bài 4 trang 14 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau:

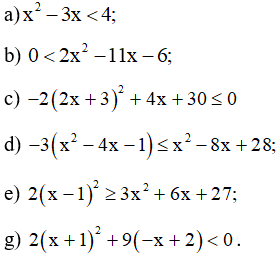
Lời giải:

a) Ta có: $x^2-3x<4$ ⟺ x² – 3x – 4 < 0

Xét tam thức bậc hai f(x) = x² – 3x – 4 có ∆ = (– 3)² – 4.1.(– 4) = 25 > 0 nên f(x) có hai nghiệm phân biệt x₁ = 4 và x₂ = –1.

Ta có: a = 1 > 0 nên f ( x ) < 0 với –1 < x < 4.

Suy ra x² – 3x – 4 < 0 hay $x^2-3x<4$ với –1 < x < 4.

Vậy bất phương trình đã cho có tập nghiệm khi S = (–1 ; 4).

b) Ta có: 0 < 2x² – 11x – 6 ⇔ 2x² – 11x – 6 > 0

Tam thức bậc hai f( x ) = 2x² – 11x – 6 có ∆ = (– 11)² – 4.2.(– 6) = 169 > 0 nên f(x) có hai nghiệm phân biệt x₁ = 6 và x₂ = $\frac{-1}{2}$,

Ta lại có: a = 2 > 0 nên f ( x ) > 0 khi x < $\frac{-1}{2}$ hoặc x > 6.

Vậy tập nghiệm của bất phương trình là: S =  (– ∞; $\frac{-1}{2}$) ∪ (6; +∞).

c) $-2{\left(2x+3\right)}^2+4x+30\le 0$ 

⟺ –2.( 4x² + 12x + 9 ) + 4x + 30 ≤ 0

⟺ –8x² – 24x – 18 + 4x + 30 ≤ 0

⟺ –8x² – 20x + 12 ≤ 0

⟺ –2x² – 5x + 3 ≤ 0

Tam thức bậc hai f ( x ) = –2x² – 5x + 3 có ∆ = (– 5)² – 4.(– 2).3 = 49 nên f(x) có hai nghiệm phân biệt x₁ = –3 và x₂ = $\frac{1}{2}$,

Ta lại có a = –2 < 0 nên f ( x ) ≤ 0 khi x ≤ –3 hoặc x ≥ $\frac{1}{2}$

Vậy bất phương trình đã cho có tập nghiệm là S = (–∞ ; –3] ∪ [$\frac{1}{2}$; +∞).

d) $-3\left(x^2-4x-1\right)\le x^2-8x+28$

⟺ –4x² + 20x – 25 ≤ 0

Tam thức bậc hai f ( x ) = –4x² + 20x – 25 có ∆ = 20² – 4. ( –4 ) . ( – 25 ) = 0 ,

a = –4 < 0 nên f ( x ) ≤  0 với mọi x ∈ ℝ.

Suy ra –4x² + 20x – 25 ≤ 0 với mọi x ∈ ℝ.

Vậy $-3\left(x^2-4x-1\right)\le x^2-8x+28$ với mọi x ∈ ℝ.

e) $2{\left(x-1\right)}^2\ge 3x^2+6x+27$

⟺ 2x² – 4x + 2 ≥ 3x²  + 6x + 27

⟺ –x² – 10x – 25 ≥ 0

⟺ –( x + 5 )² ≥ 0

⟺ x = –5 ( do –( x + 5 )² ≤ 0 với mọi x ∈ ℝ)

Vậy $2{\left(x-1\right)}^2\ge 3x^2+6x+27$ khi x = –5

g) $2{\left(x+1\right)}^2+9\left(-x+2\right)<0$

⇔ 2(x² + 2x + 1) – 9x + 18 < 0

⇔ 2x² – 5x + 20 < 0

Tam thức bậc hai f ( x ) = 2x² – 5x + 20 có ∆ = (– 5)² – 4. 2 . 20 = –135 < 0,

Ta lại có a = 2 > 0 nên f ( x ) > 0 với mọi x ∈ ℝ.

Suy ra 2x² – 5x + 20 > 0 với mọi x ∈ ℝ.

Vậy không tồn tại x thỏa mãn $2{\left(x+1\right)}^2+9\left(-x+2\right)<0$.

Bài 5 trang 14 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:

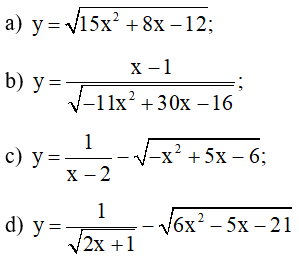
Lời giải:

a) Hàm số xác định khi và chỉ khi 15x² + 8x – 12 ≥ 0

Tam thức bậc hai f ( x ) = 15x² + 8x – 12 có ∆ = 8² – 4.15. (–12) = 784 > 0 suy ra f(x) có hai nghiệm phân biệt x₁ = $\frac{2}{3}$ và x₂ = $\frac{-6}{5}$.

Ta có: a = 15 > 0 nên f ( x ) ≥ 0 khi và chỉ khi x ≤ $\frac{-6}{5}$ hoặc x ≥ $\frac{2}{3}$.

Vậy tập xác định của hàm số là D = $\left(-\infty ;\frac{-6}{5}\right]\cup \left[\frac{2}{3};+\infty \right)$.

b) Hàm số xác định khi và chỉ khi –11x² + 30x – 16 > 0

Tam thức bậc hai f ( x ) = –11x² + 30x – 16 có ∆ = 30² – 4.( –11).( –16) =  196 > 0 suy ra f(x) có hai nghiệm phân biệt x₁ = 2 và x₂ = $\frac{8}{11}$.

Ta có: a = –11 < 0 nên f ( x ) > 0 khi và chỉ khi $\frac{8}{11}$ < x < 2.

Vậy tập xác định của hàm số là D = $\left(\frac{8}{11};2\right)$.

c) Hàm số xác định khi và chỉ khi x – 2 ≠ 0 và –x² + 5x – 6 ≥ 0.

+) Xét x – 2 ≠ 0 khi và chỉ khi x ≠ 2.

+) Xét tam thức bậc hai f ( x ) = –x² + 5x – 6 có ∆ = 5² – 4.( –1).( –6) = 1 > 0 suy ra f(x) hai nghiệm phân biệt x₁ = 3 và x₂ = 2 ,

Ta có: a = –1 < 0 nên f ( x ) ≥ 0 khi và chỉ khi 2 ≤ x ≤ 3.

Suy ra hàm số xác định khi 2 < x ≤ 3.

Vậy tập xác định của hàm số là D = $\left(2;3\right]$.

d) Hàm số xác định khi và chỉ khi 2x + 1 > 0 và 6x² – 5x – 21 ≥ 0

+) Xét 2x + 1 > 0 khi và chỉ khi x > $\frac{-1}{2}$

+) Xét tam thức bậc hai f ( x ) = 6x² – 5x – 21 có ∆ = (–5)² – 4.6.( –21) = 529 > 0 suy ra f(x) hai nghiệm phân biệt x₁ = $\frac{7}{3}$ và x₂ = $\frac{-3}{2}$ ,

Ta có a = 6 > 0 nên f ( x ) ≥ 0 khi và chỉ khi x ≤ $\frac{-3}{2}$ hoặc x ≥ $\frac{7}{3}$ mà x > $\frac{-1}{2}$ nên x ≥ $\frac{7}{3}$.

Vậy tập xác định của hàm số là D = $\left[\frac{7}{3};+\infty \right)$.

Bài 6 trang 14 SBT Toán 10 Tập 2: Tìm giá trị của tham số m để:

a) x = 3 là một nghiệm của bất phương trình $\left(m^2-1\right)x^2+2mx-15\le 0$;

b) x = -1 là một nghiệm của bất phương trình $m{x}^2-2x+1>0$;

c) $x=\frac{5}{2}$ là một nghiệm của bất phương trình $4x^2+2mx-5m\le 0$;

d) x = -2 là một nghiệm của bất phương trình $\left(2m-3\right)x^2-\left(m^2+1\right)x\ge 0$;

e) x = m + 1 là một nghiệm của bất phương trình $2x^2+2mx-m^2-2<0$.

Lời giải:

a) x = 3 là một nghiệm của bất phương trình $\left(m^2-1\right)x^2+2mx-15\le 0$ khi và chỉ khi (m² – 1 ).3² + 2m.3 – 15 ≤ 0 hay 9m² + 6m – 24 ≤ 0

Tam thức bậc hai f (m) = 9m² + 6m – 24 có ∆ = 6² – 4.9.( –24) = 900 suy ra hai nghiệm phân biệt m₁ = $\frac{4}{3}$ và m₂ = –2 và a = 9 > 0 nên f ( m ) ≤ 0 khi và chỉ khi – 2 ≤ m ≤ $\frac{4}{3}$.

Vậy – 2 ≤ m ≤ $\frac{4}{3}$ thỏa mãn yêu cầu đề bài.

b) x = -1 là một nghiệm của bất phương trình $m{x}^2-2x+1>0$ khi và chỉ khi

m.(–1 )² – 2.(–1 ) + 1 > 0 hay m + 3 > 0 hay m > –3.

Vậy m > –3 thỏa mãn yêu cầu đề bài.

c) $x=\frac{5}{2}$ là một nghiệm của bất phương trình $4x^2+2mx-5m\le 0$ khi và chỉ khi

4.${\left(\frac{5}{2}\right)}^2$+ 2.m.$\frac{5}{2}$ – 5m ≤ 0 hay 25 ≤ 0 ( vô lí ).

Vậy không có giá trị m thỏa mãn yêu cầu đề bài.

d) x = -2 là một nghiệm của bất phương trình $\left(2m-3\right)x^2-\left(m^2+1\right)x\ge 0$ khi và chỉ khi ( 2m – 3 ). ( –2)² – (m² + 1 ).( –2) ≥ 0 hay 2m² + 8m – 10 ≥ 0

Tam thức bậc hai f (m) = 2m² + 8m – 10 có ∆ = 8² – 4.2.( –10) = 144 suy ra f(m) có hai nghiệm phân biệt m₁ = –5 và m₂ = 1 và a = 2 > 0 nên f ( m )  ≥  0 khi và chỉ khi

m ≤ –5 hoặc m ≥ 1.

Vậy m ≤ –5 hoặc m ≥ 1 thỏa mãn yêu cầu đề bài.

e) x = m + 1 là một nghiệm của bất phương trình $2x^2+2mx-m^2-2<0$ khi và chỉ khi 2.(m+1)² + 2m.(m+1) – m² – 2 < 0 hay 3m² + 6m < 0

Tam thức bậc hai f (m) = 3m² + 6m có ∆ = 6² – 4.3.0 = 36 suy ra hai nghiệm phân biệt m₁ = –2 và m₂ = 0 và a = 2 > 0 nên f ( m )  <  0 khi và chỉ khi –2 < m < 0.

Vậy –2 < m < 0 thỏa mãn yêu cầu đề bài.

Bài 7 trang 14 SBT Toán 10 Tập 2: Với giả trị nào của tham số m thì:

a) Phương trình $4x^2+2\left(m-2\right)x+m^2=0$ có nghiệm;

b) Phương trình $\left(m+1\right)x^2+2mx-4=0$ có hai nghiệm phân biệt;

c) Phương trình $m{x}^2+\left(m+1\right)x+3m+10=0$vô nghiệm,

d) Bất phương trình $2x^2+\left(m+2\right)x+\left(2m-4\right)\ge 0$ có tập nghiệm là $ℝ$;

e) Bất phương trình $-3x^2+2mx+m^2\ge 0$ có tập nghiệm là $ℝ$.

Lời giải:

a) Phương trình $4x^2+2\left(m-2\right)x+m^2=0$ có nghiệm khi và chỉ khi:

∆ = [2.( m – 2 )]² – 4.4.m² ≥ 0

⇔ m² – 4m + 4 – 4m² ≥ 0

⇔ – 3m² – 4m + 4 ≥ 0

Tam thức bậc hai f (m) = – 3m² – 4m + 4 có ∆_m = (–4)² – 4.( –3).4 = 64 > 0 suy ra f(m) có hai nghiệm phân biệt m₁ =  và m₂ = –2,  a = – 3 < 0 nên f (m) ≥ 0 khi và chỉ khi – 2 ≤ m ≤ $\frac{2}{3}$.

Vậy – 2 ≤ m ≤  thỏa mãn yêu cầu đề bài.

b) Phương trình $\left(m+1\right)x^2+2mx-4=0$ có hai nghiệm phân biệt khi và chỉ khi

m + 1 ≠ 0 và ∆ = (2m)² – 4.( m+1 ).(–4) > 0

+) Ta có: m + 1 ≠ 0 khi và chỉ khi m ≠ –1.

+) Xét ∆ = (2m)² – 4.(m+1).(–4) > 0

⟺ 4m² + 16m + 16 > 0

⟺  m² + 4m + 4 > 0

⟺ ( m + 2 )² > 0

⟺ m ≠ –2 (vì ( m + 2 )² ≥ 0 với mọi x ∈ ℝ)

Vậy m ≠ –1 và m ≠ –2 thỏa mãn yêu cầu bài toán.

c) +) Nếu m = 0 thì phương trình trở thành x + 10 = 0, có nghiệm x = –10. Do đó m = 0 không thỏa mãn yêu cầu.

+) Nếu m ≠ 0 thì phương trình vô nghiệm khi và chỉ khi:

∆ = (m + 1)² – 4.m.( 3m + 10 ) < 0

⟺ m² + 2m + 1 – 12m² – 40m < 0

⟺ –11m² – 38m +1 < 0

Tam thức bậc hai f (m) = –11m² – 38m +1 có ∆_m = (–38)2 – 4.( –11).1 = 1488  suy ra f(m) có hai nghiệm phân biệt:

m₁ = $\frac{-19+2\sqrt{93}}{11}$ và  m₂ = $\frac{-19-2\sqrt{93}}{11}$,  a = – 11 < 0 nên f ( m ) < 0 khi và chỉ khi

m < $\frac{-19-2\sqrt{93}}{11}$ hoặc m > $\frac{-19+2\sqrt{93}}{11}$

Vậy m < $\frac{-19-2\sqrt{93}}{11}$ và m > $\frac{-19+2\sqrt{93}}{11}$ thoả mãn yêu cầu đề bài.

d) Bất phương trình $2x^2+\left(m+2\right)x+\left(2m-4\right)\ge 0$ có a = 2 > 0 nên tập nghiệm là $\mathrm{ℝ}$ khi và chỉ khi ∆ = ( m + 2 )² – 4.2.( 2m – 4 ) ≤ 0

⟺ m² + 4m + 4 – 16m+ 32 < 0

⟺ m² – 12m + 36 ≤ 0

⟺ ( m – 6 )²  ≤ 0

⟺ m = 6 (vì ( m – 6 )²  ≥ 0 với mọi m ∈ ℝ)

Vậy m = 6 thỏa mãn yêu cầu đề bài.

e) Bất phương trình $-3x^2+2mx+m^2\ge 0$ có tập nghiệm là $\mathrm{ℝ}$ khi và chỉ khi a > 0 và ∆ ≤ 0 mà a = –3 < 0 nên không tồn tại m thỏa mãn yêu cầu.

Vậy không tồn tại m thỏa mãn yêu cầu.

Bài 8 trang 14 SBT Toán 10 Tập 2: Lợi nhuận thu được từ việc sản xuất và bán x sản phẩm thủ công của một cửa hàng là:

$I\left(x\right)=-0,1x^2+235x-70000,$

với I được tính bằng nghìn đồng. Với số lượng sản phẩm bán ra là bao nhiêu thì cửa hàng có lãi?

Lời giải:

Cửa hàng có lãi khi và chỉ khi I ( x ) > 0 hay –0,1x² + 235x – 70000 > 0

Tam thức bậc hai $I\left(x\right)=-0,1x^2+235x-70000,$ có ∆ = 235² – 4.(– 0,1).(– 70 000) = 27 225 > 0  nên I(x) có hai nghiệm phân biệt x₁ = 2000 và x₂ = 350, a = –0,1 < 0 nên I ( x ) > 0 khi 350 < x < 2000.

Vậy cửa hàng bán ra từ 351 đến 1999 sản phẩm thì cửa hàng có lãi.

Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 13 Tập 2

Giải SBT Toán 10 trang 15 Tập 2