Câu hỏi:
06/01/2025 19,446Cho tanα = 3. Tính giá trị của biểu thức 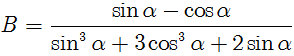
A. 1
B. 2
C. 2/9
D. 4/9
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là : C
*Lời giải
Vì tanx xác định nên cosx ≠ 0. Chia tử và mẫu của phân thức cho luỹ thừa thích hợp của cosx để biểu diễn biểu thức theo tanx.
Suy ra
*Phương pháp giải
Biến đổi biểu thức đã cho về tỉ số lượng giác cho trước (sử dụng công thức ).
*Lý thuyết
1. Đồ thị và tính chất của hàm số y = sinx
- Tập xác định là .
- Tập giá trị là [-1;1].
- Là hàm số lẻ và tuần hoàn chu kì 2.
- Đồng biến trên mỗi khoảng và nghịch biến trên mỗi khoảng
- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
2. Đồ thị và tính chất của hàm số y = cosx
Tập xác định là .
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2.
Đồng biến trên mỗi khoảng và nghịch biến trên mỗi khoảng .
Có đồ thị là một đường hình sin đối xứng qua trục tung.
Hệ quả:
+) xác định với mọi giá trị của và .
+) được xác định khi , xác định khi
+)
+) Dấu của các giá trị lượng giác phụ thuộc vào vị trí điểm M nằm trên đường tròn lượng giác.
Ta có bảng xác định dấu của các giá trị lượng giác:
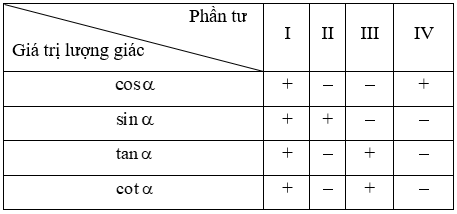
Các công thức lượng giác cơ bản:

Các dạng bài
Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị
a. Phương pháp giải:
Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.
Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
Dạng 3: Rút gọn biểu thức lượng giác
a. Phương pháp giải:
Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
Xem thêm
Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án
Giá trị lượng giác của cung và cách giải bài tập (2024) chi tiết nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho A: B; C là các góc nhọn và tanA = 1/2, tanB = 1/5, tanC = 1/8,. Tổng A + B + C bằng
Câu 3:
Cho góc α thỏa mãn ![]() và sinα + cosα > 0. Tính P = sin3 α + cos3 α.
và sinα + cosα > 0. Tính P = sin3 α + cos3 α.
Câu 8:
Biết OMB’ và ONB’ là các tam giác đều. Cung α có mút đầu là A và mút cuối là B hoặc M hoặc N. Tính số đo của α?
Câu 9:
Trong mặt phẳng định hướng cho tia Ox và hình vuông OABC vẽ theo chiều ngược với chiều quay của kim đồng hồ, biết sđ ( Ox; OA) = 300 + k.3600 . Khi đó sđ (Ox; BC) bằng:
Câu 11:
Biểu thức A = cos (-530) .sin( -3370) + sin3070.sin 1130 có giá trị bằng:
Câu 13:
Trong mặt phẳng định hướng cho tia Ox và hình vuông OABC vẽ theo chiều ngược với chiều quay của kim đồng hồ, biết sđ( Ox; OA) = 300 + k.3600. Khi đó sđ ( OA; AC) bằng:
Câu 15:
Một đường tròn có bán kính 15 cm . Tìm độ dài cung tròn có góc ở tâm bằng 300 là :

 là
là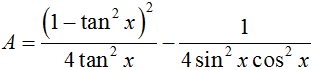
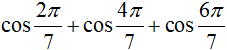 bằng :
bằng :
