Biểu thức $2\cos \frac{\mathrm{\pi }}{7}\cos \frac{2\mathrm{\pi }}{7}+\cos \frac{4\mathrm{\pi }}{7}+\cos \frac{6\mathrm{\pi }}{7}$ bằng

Đáp án đúng: C

* Lời giải:

$$\begin{gathered} 2\cos \frac{\mathrm{\pi }}{7}.\cos \frac{2\mathrm{\pi }}{7}+\cos \frac{4\mathrm{\pi }}{7}+\cos \frac{6\mathrm{\pi }}{7} \\ =2\cos \frac{\mathrm{\pi }}{7}.\cos \frac{2\mathrm{\pi }}{7}+2\cos \frac{5\mathrm{\pi }}{7}\cos \frac{\mathrm{\pi }}{7} \\ =2\cos \frac{\mathrm{\pi }}{7}\left(\cos \frac{2\mathrm{\pi }}{7}+\cos \frac{5\mathrm{\pi }}{7}\right) \\ =4\cos \frac{\mathrm{\pi }}{7}\cos \frac{\mathrm{\pi }}{2}\cos \frac{3\mathrm{\pi }}{14} \\ =4\cos \frac{\mathrm{\pi }}{7}.0.\cos \frac{3\mathrm{\pi }}{14}=0 \end{gathered}$$

*Phương pháp giải:

Áp dụng các công thức về lượng giác để biến đổi và thực hiện phép tính

*Lý thuyết cần nắm và các dạng bài tập về giá trị lượng giác: 

1. Đồ thị và tính chất của hàm số y = sinx

- Tập xác định là $\mathbb{R}$.

- Tập giá trị là [-1;1].

- Là hàm số lẻ và tuần hoàn chu kì 2$\pi$.

- Đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k2\pi ;\frac{\pi }{2}+k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left(\frac{\pi }{2}+k2\pi ;\frac{3\pi }{2}+k2\pi \right)$

- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

2. Đồ thị và tính chất của hàm số y = cosx

Tập xác định là $\mathbb{R}$.

Tập giá trị là [-1;1].

Là hàm số chẵn và tuần hoàn chu kì 2$\pi$.

Đồng biến trên mỗi khoảng $\left(-\pi +k2\pi ;k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left(k2\pi ;\pi +k2\pi \right)$.

Có đồ thị là một đường hình sin đối xứng qua trục tung.

Hệ quả:

+) $\sin \alpha ,\cos \alpha$ xác định với mọi giá trị của $\alpha$ và $-1\le \sin \alpha \le 1,-1\le \cos \alpha \le 1$.

+) $\tan \alpha$ được xác định khi $\alpha \ne \frac{\pi }{2}+k\pi$, xác định khi $\alpha \ne k\pi$

+) $\sin \alpha =\sin \left(\alpha +k2\pi \right),\cos \alpha =\cos \left(\alpha +k2\pi \right)$

$\tan \alpha =\tan \left(\alpha +k\pi \right),\cot \alpha =\cot \left(\alpha +k\pi \right)$

+) Dấu của các giá trị lượng giác phụ thuộc vào vị trí điểm M nằm trên đường tròn lượng giác.

Ta có bảng xác định dấu của các giá trị lượng giác:

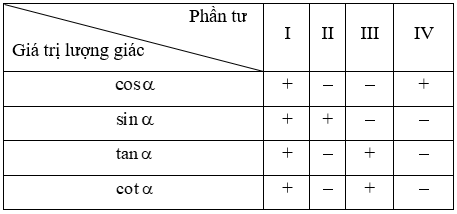
Các công thức lượng giác cơ bản:

Các dạng bài

Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị

a. Phương pháp giải:

Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.

Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác

a. Phương pháp giải:

Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.

Ta lựa chọn một trong các cách biến đổi sau:

* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)

* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.

* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.

Dạng 3: Rút gọn biểu thức lượng giác

a. Phương pháp giải:

Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.

Xem thêm các bài viết liên quan hay, chi tiết:

Tổng hợp bảng giá trị lượng giác

Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án

Giá trị lượng giác của cung và cách giải bài tập (2024) chi tiết nhất