Nội dung bài viết

    Xem thêm

    Lý thuyết Phương trình mặt cầu – Toán lớp 12 Kết nối tri thức

    Với lý thuyết Toán lớp 12 Bài 17:  Phương trình mặt cầu chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 12.

    1 223 15/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 12 Bài 17: Phương trình mặt cầu- Kết nối tri thức

    A. Lý thuyết Phương trình mặt cầu

    1. Phương trình mặt cầu

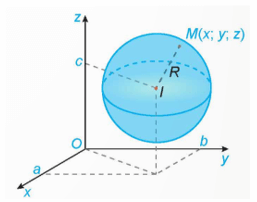
    Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c) bán kính R có phương trình:

    (x – a)2 + (y – b)2 + (z – c)2 = R2.

    Phương trình mặt cầu (Lý thuyết Toán lớp 12) | Kết nối tri thức

    Chú ý

    +) Điểm M(x; y; z) nằm trong mặt cầu (S) nếu (x – a)2 + (y – b)2 + (z – c)2 < R2.

    +) Điểm M(x; y; z) nằm ngoài mặt cầu (S) nếu (x – a)2 + (y – b)2 + (z – c)2 > R2.

    Ví dụ 1. Trong không gian Oxyz, viết phương trình mặt cầu (S) có tâm I(1; −4; 0) và bán kính bằng 3.

    Hướng dẫn giải

    Phương trình mặt cầu là: (x – 1)2 + (y + 4)2 + z2 = 9.

    Nhận xét. Với a, b, c, d là các hằng số, phương trình x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 có thể viết lại thành (x – a)2 + (y – b)2 + (z – c)2 = a2 + b2 + c2 – d và là phương trình của một mặt cầu (S) khi và chỉ khi a2 + b2 + c2 – d > 0. Khi đó, (S) có tâm I(a; b; c) và bán kính R=a2+b2+c2−d

    Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, phương trình nào trong các phương trình sau là phương trình của mặt cầu. Xác định tâm và bán kính của mặt cầu ứng với phương trình đó.

    a) x2 + y2 + z2 + x – 2y + 4z – 3 = 0.

    b) x2 + y2 + z2 – 2x + 4y – 4z + 10 = 0.

    Hướng dẫn giải

    a) Phương trình đã cho tương ứng với a=−12 ; b = 1; c = −2 và d = −3.

    Có a2 + b2 + c2 – d = 334>0 .

    Do đó đây là phương trình mặt cầu với tâm I−12;1;−2;R=332 .

    b) Phương trình đã cho tương ứng với a = 1; b = −2; c = 2; d = 10.

    Có a2 + b2 + c2 – d = −1 < 0 nên đây không phải là phương trình mặt cầu.

    B. Bài tập Phương trình mặt cầu

    Bài 1. Trong không gian Oxyz, cho mặt cầu (S): (x – 2)2 + (y + 1)2 + (z – 3)2 = 4. Tâm của (S) có tọa độ là

    A. (−2; 1; −3).

    B. (−4; 2; −6).

    C. (4; −2; 6).

    D. (2; −1; 3).

    Hướng dẫn giải

    Đáp án đúng là: D

    Mặt cầu (S) có tâm I(2; −1; 3).

    Bài 2. Trong không gian Oxyz, xác định phương trình mặt cầu (S) biết:

    a) mặt cầu (S) có tâm A(2; 1; 0), đi qua điểm B(0; 1; 2).

    b) mặt cầu (S) có đường kính AB với A(1; 2; 3), B(5; 4; −1).

    Hướng dẫn giải

    a) Ta có R = AB = 0−22+1−12+2−02=22 .

    Phương trình mặt cầu cần tìm là: (x – 2)2 + (y – 1)2 + z2 = 8.

    b) Gọi I(3; 3; 1) là trung điểm của AB,

    R=AB2=5−12+4−22+−1−322=3 .

    Phương trình mặt cầu cần tìm là: (x – 3)2 + (y – 3)2 + (z – 1)2 = 9.

    Bài 3. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z2 – 2x – 2y – 2z – 22 = 0 và mặt phẳng (P): 3x – 2y + 6z + 14 = 0. Tính khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (P).

    Hướng dẫn giải

    Mặt cầu (S) có tâm là I(1; 1; 1).

    Có dI,P=3.1−2.1+6.1+1432+−22+62=217=3 .

    Bài 4. Trong không gian hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là kilômét) một trạm phát sóng rađa của Nga được đặt trên bán đảo Crimea ở vị trí I(−2; 1; −1) và được thiết kế phát hiện máy bay của địch ở khoảng cách tối đa 500 km.

    a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng của rađa trong không gian.

    b) Hai chiếc máy bay do thám của Mỹ và Anh đang bay ở vị trí có tọa độ lần lượt là M(−200; 100; −250) và N(350; −100; 300). Hỏi rađa của Nga có thể phát hiện ra hai chiếc máy bay do thám của Mỹ và Anh không?

    Hướng dẫn giải

    a) Phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng của rađa trong không gian là (x + 2)2 + (y – 1)2 + (z + 1)2 = 250000.

    b)

    Có IM=−200+22+100−12+−250+12≈333,18<R .

    IN=350+22+−100−12+300+12≈474,03<R.

    Vậy rađa của Nga có thể phát hiện ra hai chiếc máy bay do thám của Mỹ và Anh.

    Bài 5. Trong không gian Oxyz, cho mặt cầu (S): x2 + (y – 2)2 + (z + 1)2 = 6. Đường kính của (S) bằng

    A. 6 .

    B. 12.

    C. 26 .

    D. 3.

    Hướng dẫn giải

    Đáp án đúng là: C

    Mặt cầu (S) có bán kính là 6 . Suy ra đường kính là 26 .

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 223 15/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: