Lý thuyết Công thức xác suất toàn phần và công thức Bayes Toán lớp 12 (Kết nối tri thức)

Lý thuyết Toán 12 Bài 19: Công thức xác suất toàn phần và công thức Bayes- Kết nối tri thức

A. Lý thuyết Công thức xác suất toàn phần và công thức Bayes

1. Công thức xác suất toàn phần

Cho hai biến cố A và B. Khi đó, ta có công thức sau:

$P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)$.

Công thức trên được gọi là công thức xác suất toàn phần.

Ví dụ 1. Giả sử tỉ lệ người dân của tỉnh Khánh Hòa nghiện thuốc lá là 20%, tỉ lệ người bị bệnh phổi trong số người nghiện thuốc lá là 70%, trong số người không nghiện thuốc lá là 15%. Hỏi khi ta gặp ngẫu nhiên một người dân của tỉnh Khánh Hòa thì khả năng người đó bị bệnh phổi là bao nhiêu %?

Hướng dẫn giải

Gọi biến cố A: “Người dân đó nghiện thuốc lá”.

Biến cố B: “Người dân đó bị bệnh phổi”.

Cần tính P(B).

Theo đề, ta có P(A) = 0,2$\Rightarrow P\left(\overline{A}\right)=0,8$ .

Lại có tỉ lệ người bị bệnh phổi trong số người nghiện thuốc lá là 70%, trong số người không nghiện thuốc là là 15% nên P(B|A) = 0,7; $P\left(B|\overline{A}\right)=0,15$ .

Theo công thức xác suất toàn phần ta có:

$P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)$

$=0,2.0,7+0,8.0,15=0,26$

Vậy khi ta gặp ngẫu nhiên một người dân của tỉnh Khánh Hòa thì khả năng người đó bị bệnh phổi là 26%.

Chú ý. Một phương pháp mô tả trực quan công thức xác suất toàn phần là dùng sơ đồ hình cây.

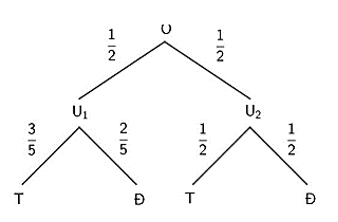
Ví dụ 2. Cho hai hộp U₁ và U₂ giống nhau về kích thước và màu sắc bên ngoài. Trong đó hộp U₁ chứa 3 quả cầu trắng, 2 quả cầu đen và hộp U₂ chứa 2 quả cầu trắng, 2 quả cầu đen. Chọn ngẫu nhiên 1 quả cầu. Tính xác suất để quả cầu lấy ra là màu trắng

Hướng dẫn giải

Ta dùng sơ đồ cây để minh họa như sau

Dựa vào sơ đồ cây, ta có xác suất để quả cầu lấy ra là màu trắng là:

$\frac{3}{5}.\frac{1}{2}+\frac{1}{2}.\frac{1}{2}=\frac{11}{20}$.

2. Công thức Bayes

Cho A và B là hai biến cố, với P(B) > 0. Khi đó ta có công thức sau:

$P\left(A|B\right)=\frac{P\left(A\right).P\left(B|A\right)}{P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)}$.

Công thức trên có tên là công thức Bayes.

Chú ý. Theo công thức xác suất toàn phần, ta có:

$P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)$.

Do đó, công thức Bayes còn có thể viết dưới dạng

$P\left(A|B\right)=\frac{P\left(A\right).P\left(B|A\right)}{P\left(B\right)}$ .

Ý nghĩa của công thức Bayes: Một nhà nghiên cứu quan tâm đến xác suất xảy ra của biến cố A. Theo tính toán ban đầu A có xác suất là P(A) = p. Sau đó, nhà nghiên cứu có được thông tin rằng: “Biến cố B đã xảy ra”. Với thông tin mới này, nhà nghiên cứu sẽ cập nhật hiểu biết của mình về khả năng xảy ra biến cố A, bằng cách tính P(A| B), xác suất của A khi biết B đã xảy ra. Công thức Bayes giúp ta tính P(A| B).

Ví dụ 3. Từ một hộp có 50 quả cầu trắng và 100 quả cầu đen. Người ta rút ngẫu nhiên không hoàn lại từng quả một và rút hai lần. Tính xác suất để lần đầu rút được quả trắng biết lần thứ hai cũng rút được quả trắng.

Hướng dẫn giải

Gọi biến cố A: “Lần đầu rút được quả trắng”.

Biến cố B: “Lần thứ hai rút được quả trắng”.

Ta cần tính P(A|B).

Theo đề ta có: $P\left(A\right)=\frac{50}{150}$; $P\left(B|A\right)=\frac{49}{149}$.

Suy ra $P\left(\overline{A}\right)=\frac{100}{150}$; $P\left(B|\overline{A}\right)=\frac{50}{149}$.

Do đó $P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)$

$=\frac{50}{150}.\frac{49}{149}+\frac{100}{150}.\frac{50}{149}=\frac{1}{3}$.

Suy ra

$P\left(A|B\right)=\frac{P\left(A\right).P\left(B|A\right)}{P\left(B\right)}$ $=\frac{50}{150}.\frac{49}{149}:\frac{1}{3}=\frac{49}{149}$ .

B. Bài tập Công thức xác suất toàn phần và công thức Bayes

Cho hai biến cố A và B, với P(B) = 0,8; P(A| B) = 0,7; $P\left(A|\overline{B}\right)=0,45$.

(Sử dụng cho bài 1, 2)

Bài 1. Tính P(A).

A. 0,25.

B. 0,65.

C. 0,55.

D. 0,5.

Hướng dẫn giải

Đáp án đúng là: B

Vì P(B) = 0,8 suy ra $P\left(\overline{B}\right)=0,2$.

Có $P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)$= 0,8.0,7 + 0,2.0,45 = 0,65.

Bài 2. Tính P(B| A).

A. 0,25.

B. 0,65.

C. $\frac{56}{65}$.

D. 0,5.

Hướng dẫn giải

Đáp án đúng là: C

Có $P\left(B|A\right)=\frac{P\left(B\right).P\left(A|B\right)}{P\left(A\right)}=\frac{0,8.0,7}{0,65}=\frac{56}{65}$.

Bài 3. Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên một viên bi từ hộp I bỏ sang hộp II. Sau đó lấy ngẫu nhiên 1 viên bi từ hộp II.

a) Tính xác suất để viên bi được lấy ra từ hộp II là viên bi màu trắng.

b) Giả sử viên bi được lấy ra từ hộp II là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I.

Hướng dẫn giải

a) Gọi A là biến cố: “Lấy được viên bi màu trắng từ hộp thứ I”.

B là biến cố: “Lấy được viên vi màu trắng từ hộp thứ II”.

Cần tính P(B).

Theo đề ta có: $P\left(A\right)=\frac{5}{10}=\frac{1}{2}$$\Rightarrow P\left(\overline{A}\right)=\frac{1}{2}$.

Có $P\left(B|A\right)=\frac{7}{11}$; $P\left(B|\overline{A}\right)=\frac{6}{11}$.

Ta có

$P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)$$\frac{1}{2}.\frac{7}{11}+\frac{1}{2}.\frac{6}{11}=\frac{13}{22}$.

b) Cần tính P(A| B).

Có $P\left(A|B\right)=\frac{P\left(A\right).P\left(B|A\right)}{P\left(B\right)}$$=\frac{1}{2}.\frac{7}{11}:\frac{13}{22}=\frac{7}{13}$.

Bài 4. Một công ty một ngày sản xuất được 850 sản phẩm trong đó có 50 sản phẩm không đạt chất lượng. Lần lượt lấy ra ngẫu nhiên không hoàn lại 2 sản phẩm để kiểm tra.

a) Tính xác suất để sản phẩm thứ hai không đạt chất lượng biết sản phẩm thứ nhất đạt chất lượng.

b) Tính xác suất để sản phẩm thứ hai không đạt chất lượng.

Hướng dẫn giải

a) Gọi biến cố A: “Sản phẩm thứ nhất đạt chất lượng”.

Biến cố B: “Sản phẩm thứ hai không đạt chất lượng”.

Cần tính P(B| A).

Do sản phẩm thứ nhất đạt chất lượng nên $P\left(B|A\right)=\frac{50}{849}$ .

b) Cần tính P(B).

Ta có $P\left(A\right)=\frac{800}{850}$ ; $P\left(\overline{A}\right)=\frac{50}{850}$ ; $P\left(B|A\right)=\frac{50}{849}$ ; $P\left(B|\overline{A}\right)=\frac{49}{849}$ .

Do đó $P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)$

$=\frac{800}{850}.\frac{50}{849}+\frac{50}{850}.\frac{49}{849}=\frac{1}{17}$ .

Bài 5. Một hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số viên bi màu đỏ đánh số và 50% số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số. Lấy ra ngẫu nhiên 1 viên bi trong hộp. Tính xác suất để viên bi được lấy ra có đánh số.

Hướng dẫn giải

Gọi biến cố A: “Viên bi lấy ra là màu đỏ”.

Biến cố B: “Viên bi lấy ra được đánh số”.

Ta cần tính P(B).

Theo đề ta có: $P\left(A\right)=\frac{50}{80}=\frac{5}{8}\Rightarrow P\left(\overline{A}\right)=\frac{3}{8}$;

Ta có $P\left(B|A\right)=0,6$; $P\left(B|\overline{A}\right)=0,5$.

Do đó $P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)$

$=\frac{5}{8}.0,6+\frac{3}{8}.0,5=\frac{9}{16}$ .

Trắc nghiệm: Công thức xác suất toàn phần và công thức Bayes

I. Nhận biết

Câu 1. Cho A, B là các biến cố của một phép thử T. Biết rằng $0<P\left(B\right)<1,$ xác suất của biến cố A được tính theo công thức nào sau đây?

A. $P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right).$

B. $P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(B|\overline{A}\right).$

C. $P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{A}\right).P\left(A|\overline{B}\right).$

D. $P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right).$

Câu 2. Cho A, B là các biến cố của một phép thử T. Biết rằng $0<P\left(B\right)$, xác suất để biến cố A với điều kiện biến cố B đã xảy ra được tính theo công thức nào dưới đây?

A. $P\left(A|B\right)=\frac{P\left(A\right)}{P\left(B\right)}.$

B. $P\left(A|B\right)=\frac{P\left(A\right).P\left(B|A\right)}{P\left(B\right)}.$

C. $P\left(A|B\right)=\frac{P\left(B\right).P\left(B|A\right)}{P\left(A\right)}.$

D. $P\left(A|B\right)=\frac{P\left(B\right)}{P\left(A\right)}.$

Câu 3. Cho A, B là các biến cố của một phép thử T. Biết rằng $P\left(A\right)>0$ và $0<P\left(B\right)<1.$ Xác suất của biến cố B với điều kiện biến cố A đã xảy ra được tính theo công thức nào?

A. $P\left(B|A\right)=\frac{P\left(A\right).P\left(A|B\right)}{P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)}.$

B. $P\left(B|A\right)=\frac{P\left(B\right).P\left(A|B\right)}{P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)}.$

C. $P\left(B|A\right)=\frac{P\left(B\right).P\left(A|B\right)}{P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)}.$

D. $P\left(B|A\right)=\frac{P\left(A\right).P\left(A|B\right)}{P\left(A\right).P\left(B|A\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)}.$

Câu 4. Nếu hai biến cố A, B thỏa mãn $P\left(A\right)=\mathrm{0,3,}P\left(B\right)=\mathrm{0,6}$ và $P\left(A|B\right)=\mathrm{0,4}$ thì $P\left(B|A\right)$ bằng

A. 0,5

B. 0,6

C. 0,8

D. 0,2.

Câu 5. Cho hai biến cố A, B với $P\left(B\right)=\mathrm{0,6};P\left(A|B\right)=\mathrm{0,7}$ và $P\left(A|\overline{B}\right)=\mathrm{0,4.}$ Khi đó, $P\left(A\right)$ bằng

A. 0,7

B. 0,4

C. 0,58.

D. 0,52.

II. Thông hiểu

Câu 6. Cho hai biến cố A, B với $P\left(B\right)=\mathrm{0,8};P\left(A|B\right)=\mathrm{0,7}$ và $P\left(A|\overline{B}\right)=\mathrm{0,45.}$ Tính $P\left(A\right)$

A. 0,25

B. 0,65

C. 0,55

D. 0,5.

Câu 7. Cho hai biến cố A, B với $P\left(B\right)=\mathrm{0,3};P\left(A\right)=\mathrm{0,4}$ và $P\left(A|B\right)=\mathrm{0,25.}$ Khi đó, $P\left(B|A\right)$ bằng

A. 0,1875.

B. 0,48

C. 0,333.

D. 0,95.

Câu 8. Một trường liên cấp có 3 khối gồm khối tiểu học, khối THCS và khối THPT. Tỉ lệ học sinh mỗi khối như sau: Khối tiểu học chiếm 25%, khối THCS chiếm 45%, khối THPT chiếm 30%. Xác suất học sinh tham gia ngoại khóa ở các khối tương ứng 30% khối tiểu học, 50% khối THCS, 40% khối THPT. Chọn ngẫu nhiên một học sinh trong trường. tính xác suất để học sinh được chọn tham gia hoạt động ngoại khóa.

A. 0,42.

B. 0,24.

C. 0,3

D. 0,25.

Câu 9. Một công ty du lịch bố trí chỗ cho đoàn khách tại ba khách sạn A, B, C theo tỉ lệ 20%, 50%, 30%. Tỉ lệ hỏng điều hòa ở khách sạn lần lượt là 5%, 4% và 8%. Tính xác suất để một khách nghỉ ở phòng điều hòa bị hỏng.

A. $\frac{2}{500}.$

B. $\frac{27}{500}.$

C. $\frac{7}{500}.$

D. $\frac{23}{500}.$

III. Vận dụng

Câu 10. Một chiếc hộp có 80 viên bi, trong đó 50 viên màu đỏ, 30 viên màu vàng ; các viên có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số viên bi màu đỏ đánh số và 50% viên bi màu vàng đánh số, những viên bi còn lại không đánh số. Khi đó:

a) Số viên bi màu đỏ có đánh số là 30.

b) Số viên bi màu vàng không đánh số là 15.

c) Lấy ra ngẫu nhiên một viên vi trong hộp. Xác suất để viên bi được lấy ra có đánh số là $\frac{3}{5}.$

d) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra không có đánh số là $\frac{7}{16}.$

Số mệnh đề đúng trong các mệnh đề trên là:

A. 1.

B. 2.

C. 3

D. 4.

Xem thêm tóm tắt lý thuyết Toán 12 sách Kết nối tri thức, chi tiết khác:

Lý thuyết Bài 15: Phương trình đường thẳng trong không gian

Lý thuyết Bài 16: Công thức tính góc trong không gian

Lý thuyết Bài 17: Phương trình mặt cầu

Lý thuyết Bài 18: Xác suất có điều kiện

Lý thuyết Bài 19: Công thức xác suất toàn phần và công thức Bayes

Xem thêm tài liệu Toán lớp 12:

Giải Toán 12 Bài 19: Công thức xác suất toàn phần và công thức Bayes

Giải SBT Toán 12 Bài 19: Công thức xác suất toàn phần và công thức Bayes

Giáo án Công thức xác suất toàn phần và công thức Bayes lớp 12

Giáo án điện tử Công thức xác suất toàn phần và công thức Bayes lớp 12