Lý thuyết Khoảng biến thiên và khoảng tứ phân vị– Toán lớp 12 Kết nối tri thức

Lý thuyết Toán 12 Bài 9: Khoảng biến thiên và khoảng tứ phân vị - Kết nối tri thức

A. Lý thuyết Khoảng biến thiên và khoảng tứ phân vị

1. Khoảng biến thiên

• Khoảng biến thiên của mẫu số liệu ghép nhóm

Cho mẫu số liệu ghép nhóm:

Trong đó các tần số m₁ > 0, m_k > 0 và n = m₁ + …+ m_k là cỡ mẫu.

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là R = a_{k + 1} – a₁.

Ý nghĩa: Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc. Khoảng biến thiên được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

Ví dụ 1. Thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty được cho trong bảng sau:

Thời gian	[15; 20)	[20; 25)	[25; 30)	[30; 35)	[35; 40)	[40; 45)	[45; 50)
Số nhân viên	6	14	25	37	21	13	9

Tính khoảng biến thiên R cho mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là R = 50 – 15 = 35.

2. Khoảng tứ phân vị

• Khoảng tứ phân vị của mẫu số liệu ghép nhóm

Xét mẫu số liệu ghép nhóm cho bởi Bảng 3.1.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là $∆$_Q là hiệu số giữa tứ phân vị thứ ba Q₃ và tứ phân vị thứ nhất Q₁ của mẫu số liệu đó, tức là $∆$_Q = Q₃ – Q₁.

Ý nghĩa: Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ cho khoảng tứ phân vị của mẫu số liệu gốc. Khoảng tứ phân vị cũng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.

Nhận xét: Do khoảng tứ phân vị của mẫu số liệu ghép nhóm chỉ phụ thuộc vào nửa giữa của mẫu số liệu, nên không bị ảnh hưởng bởi các giá trị bất thường và có thể dùng đại lượng này để loại giá trị bất thường.

Ví dụ 2. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Cỡ mẫu là 3 + 12 + 15 + 24 + 2 = 56.

Gọi x₁; …; x₅₆ là thời gian truy cập Internet của 56 học sinh và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.

Tứ phân vị thứ nhất là $\frac{x_{14}+x_{15}}{2}$. Do x₁₄; x₁₅ đều thuộc nhóm [12,5; 15,5) nên nhóm này chứa Q₁.

Do đó $Q_1=12,5+\frac{\frac{56}{4}-3}{12}.\left(15,5-12,5\right)=15,25$.

Với tứ phân vị thứ ba là$\frac{x_{42}+x_{43}}{2}$. Do x₄₂; x₄₃ đều thuộc nhóm [18,5; 21,5) nên nhóm này chứa Q₃.

Do đó $Q_3=18,5+\frac{\frac{56.3}{4}-30}{24}.\left(21,5-18,5\right)=20$.

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

$∆$_Q = Q₃ – Q₁ = 20 – 15,25 = 4,75.

B. Bài tập Khoảng biến thiên và khoảng tứ phân vị

Bài 1. Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

A. Hiệu giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu ghép nhóm đó.

B. Tổng giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu ghép nhóm đó.

C. Hiệu giữa hai tứ phân vị bất kì của mẫu số liệu ghép nhóm đó.

D. Tổng giữa hai tứ phân vị bất kì của mẫu số liệu ghép nhóm đó.

Hướng dẫn giải

Đáp án đúng là: A

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là hiệu giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu ghép nhóm đó.

(Dùng cho bài 2, 3) Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:

Bài 2. Tìm khoảng biến thiên của mẫu số liệu trên?

Hướng dẫn giải

Khoảng biến thiên của mẫu số liệu trên là R = 100 – 0 = 100.

Bài 3. Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên?

Hướng dẫn giải

Cỡ mẫu là n = 5 + 9 + 12 + 10 + 6 = 42.

Giả sử x₁; …; x₄₂ là thời gian tập thể dục của 42 học sinh và được xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất là x₁₁. Mà x₁₁ thuộc nhóm [20; 40) nên nhóm chứa tứ phân vị thứ nhất là [20;40).

Ta có $Q_1=20+\frac{\frac{42}{4}-5}{9}.\left(40-20\right)=\frac{290}{9}$.

Tứ phân vị thứ ba là x₃₂. Mà x₃₂ thuộc nhóm [60; 80). Do đó nhóm chứa tứ phân vị thứ ba là [60; 80).

$Q_3=60+\frac{\frac{42}{4}.3-26}{10}.\left(80-60\right)=71$.

Vậy ${\Delta }_Q=Q_3-Q_1=71-\frac{290}{9}=\frac{349}{9}$.

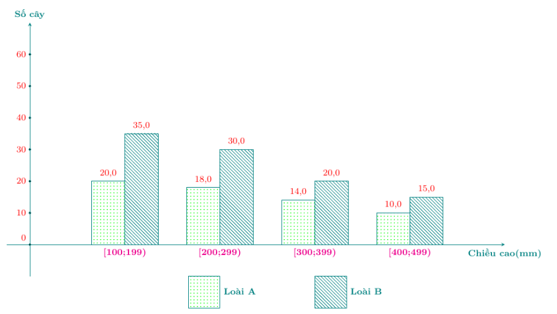
Bài 4. Chiều cao của hai loài hoa được một người thống kê theo biểu đồ sau:

Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên về chiều cao của loài hoa A và loài hoa B. Dựa vào khoảng tứ phân vị, hãy xác định xem chiều cao của loài hoa nào biến động nhiều hơn.

Hướng dẫn giải

Từ biểu đồ, ta có bảng số liệu ghép nhóm sau:

Xét loài A.

Cỡ mẫu là n = 20 + 18 + 14 + 10 = 62.

Giả sử x₁; …; x₆₂ là chiều cao của 62 cây hoa loài A và được xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất của mẫu số liệu là x₁₆ mà x₁₆ $\in$ [100; 199).

Do đó $Q_1=100+\frac{\frac{62}{4}-0}{20}.\left(199-100\right)=176,725$.

Tứ phân vị thứ ba của mẫu số liệu là x₄₇ mà x₄₇ $\in$ [300; 399).

Do đó $Q_3=300+\frac{\frac{62}{4}.3-38}{14}.\left(399-300\right)=\frac{10083}{28}$.

Vậy ${\Delta }_Q=\frac{10083}{28}-176,725\approx 183,38$.

Xét loài B.

Cỡ mẫu n = 35 + 30 + 20 + 15 = 100.

Giả sử y₁; …; y₁₀₀ là chiều cao của 100 cây hoa loài B và được sắp theo thứ tự không giảm.

Tứ phân vị thứ nhất là $\frac{y_{25}+y_{26}}{2}$, mà y₂₅; y₂₆ $\in$ [100; 199).

Ta có $Q_1=100+\frac{\frac{100}{4}-0}{35}.\left(199-100\right)=\frac{1195}{7}$.

Tứ phân vị thứ ba là $\frac{y_{25}+y_{26}}{2}$, mà y₇₅; y₇₆ $\in$ [300; 399).

Ta có $Q_3=300+\frac{\frac{100.3}{4}-65}{20}.\left(399-300\right)=\frac{699}{2}$.

Vậy ${\Delta }_Q=\frac{699}{2}-\frac{1195}{7}=\frac{2503}{14}$.

Chiều cao của loài A có độ phân tán nhiều hơn.

Bài 5. Khoảng biến thiên của mẫu số liệu ghép nhóm là:

A. Tổng số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.

B. Hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.

C. Tổng số giữa hai đầu mút của nhóm bất kì có chứa dữ liệu của mẫu số liệu.

D. Hiệu số giữa hai đầu mút của nhóm bất kì có chứa dữ liệu của mẫu số liệu.

Hướng dẫn giải

Đáp án đúng là: B

Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.