Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán lớp 12 (Kết nối tri thức)

Lý thuyết Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số- Kết nối tri thức

A. Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

1. Định nghĩa

• Khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Cho hàm số y = f(x) xác định trên tập D.

- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) $\le$ M với mọi x ∈ D và tồn tại x₀ ∈ D sao cho f(x₀) = M.

Kí hiệu $M=\underset{x_0\in D}{\max }f\left(x\right)$ hoặc $M=\underset{D}{\max }f\left(x\right)$ .

- Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) $\ge$ m với mọi x ∈ D và tồn tại x₀ ∈ D sao cho f(x₀) = m.

Kí hiệu $m=\underset{x\in D}{\min }f\left(x\right)$ hoặc $m=\underset{D}{\min }f\left(x\right)$.

Chú ý:

- Ta quy ước rằng khi nói giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) (mà không nói “trên tập D”) thì ta hiểu đó là giá trị lớn nhất hay giá trị nhỏ nhất của f(x) trên tập xác định của hàm số.

- Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập D, ta thường lập bảng biến thiên của hàm số trên tập D để kết luận.

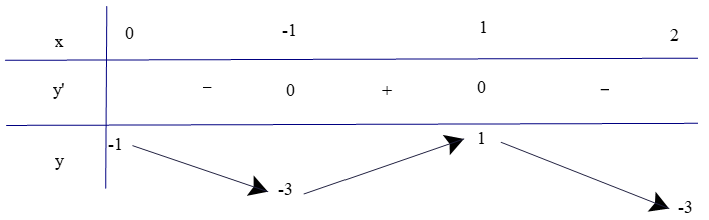
Ví dụ 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) = −x³ + 3x – 1 trên đoạn [0; 2].

Hướng dẫn giải

Trên đoạn [0; 2], có y' = −3x² + 3; y' = 0 $\iff$ x = −1 hoặc x = 1.

Bảng biến thiên

Từ bảng biến thiên, ta có:

$\underset{\left[0;2\right]}{\max }f\left(x\right)=f\left(1\right)=1$ và $\underset{\left[0;2\right]}{\min }f\left(x\right)=f\left(-1\right)=f\left(2\right)=-3$ .

Chú ý:

Trong thực hành, ta cũng dùng các kí hiệu $\underset{D}{\min }y,\underset{D}{\max }y$ để chỉ giá trị nhỏ nhất, giá trị lớn nhất (nếu có) của hàm số $y=f\left(x\right)$ trên tập D. Do đó, trong ví dụ 1 ta có thể viết: $\underset{\left[0;2\right]}{\max }y=y\left(1\right)=1$ và $\underset{\left[0;2\right]}{\min }y=y\left(-1\right)=y\left(2\right)=-3$ .

2. Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Giả sử y = f(x) là hàm số liên tục trên [a; b] và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn [a; b] mà đạo hàm f'(x) bằng 0.

Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b]:

Bước 1: Tìm các điểm x₁, x₂, …, x_n ∈ (a; b), tại đó f'(x) bằng 0 hoặc không tồn tại.

Bước 2: Tính f(x₁), f(x₂), …, f(x_n), f(a) và f(b).

Bước 3: Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có: $M=\underset{\left[a;b\right]}{\max }f\left(x\right);m=\underset{\left[a;b\right]}{\min }f\left(x\right)$ .

Ví dụ 2. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x³ – 3x² trên đoạn [1; 5].

Hướng dẫn giải

Trên đoạn [1; 5], có y' = 3x² – 6x; y' = 0 $\iff$x = 0 (loại) hoặc x = 2 (nhận).

Có y(1) = −2; y(2) = −4; y(5) = 50.

Vậy $\underset{\left[1;5\right]}{\max }y=y\left(5\right)=50;\underset{\left[1;5\right]}{\min }y=y\left(2\right)=-4$.

B. Bài tập tự luyện

Bài 1. Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y=\frac{1}{2}x-\sqrt{x+2}$ trên đoạn [−1; 34]. Tổng S = 3m + M bằng.

A. $S=\frac{13}{2}$. B. $S=\frac{25}{2}$ . C. $S=\frac{63}{2}$ . D. $S=\frac{11}{2}$ .

Hướng dẫn giải

Đáp án đúng là: A

Trên đoạn [−1; 34], có $y^{\text{'}}=\frac{1}{2}-\frac{1}{2\sqrt{x+2}}$ ;

$y^{\text{'}}=0\iff \sqrt{x+2}=1\iff x=-1$ (nhận).

Có $y\left(-1\right)=-\frac{3}{2};y\left(34\right)=11$ .

Do đó $m=-\frac{3}{2};M=11$ . Suy ra $S=3.\left(-\frac{3}{2}\right)+11=\frac{13}{2}$.

Bài 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x³ – 3x² – 9x + 5 trên đoạn [−2; 2].

Hướng dẫn giải

Trên đoạn [−2; 2], có y' = 3x² – 6x – 9; y' = 0 $\iff$ x = −1 (nhận) hoặc x = 3 (loại).

Có y(−2) = 3; y(−1) = 10; y(2) = −17.

Vậy $\underset{\left[-2;2\right]}{\max }y=y\left(-1\right)=10;\underset{\left[-2;2\right]}{\min }y=y\left(2\right)=-17$ .

Bài 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{x^2-4x}{2x+1}$ trên đoạn [0; 3].

Hướng dẫn giải

Trên đoạn [0; 3], có $y^{\text{'}}=\frac{\left(2x-4\right)\left(2x+1\right)-2\left(x^2-4x\right)}{{\left(2x+1\right)}^2}=\frac{2x^2+2x-4}{{\left(2x+1\right)}^2}$ ;

Có y' = 0 $\iff$ 2x² + 2x – 4 = 0 $\iff$ x = −2 (loại) hoặc x = 1 (nhận).

Có y(0) = 0; y (1) = −1; y(3) = $-\frac{3}{7}$ .

Vậy $\underset{\left[0;3\right]}{\max }y=y\left(0\right)=0;\underset{\left[0;3\right]}{\min }y=y\left(1\right)=-1$.

Bài 4. Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = 45t² – t³ (kết quả khảo sát được trong tháng 8 vừa qua). Nếu xem f'(t) là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Hỏi tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?

Hướng dẫn giải

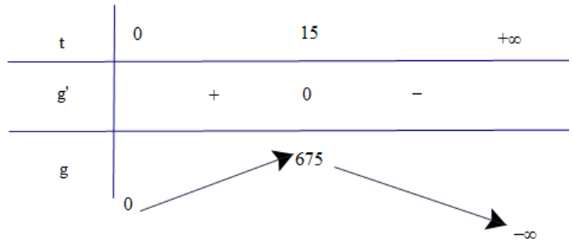
Ta có f'(t) = 90t – 3t².

Bài toán trở thành tìm giá trị lớn nhất của g(t) = f'(t) = 90t – 3t² trên (0; +∞).

Có g'(t) = 90 – 6t; g'(t) = 0 $\iff$ t = 15.

Bảng biến thiên

Dựa vào bảng biến thiên, ta có tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ 15

Bài 5. Giá trị nhỏ nhất của hàm số y = x³ + 3x² trên đoạn [−5; −1] bằng

A. 0. B. 4. C. 2. D. −50.

Hướng dẫn giải

Đáp án đúng là: D

Trên đoạn [−5; −1], có y' = 3x² + 6x;

Có y' = 0 $\iff$ x = 0 (loại) hoặc x = −2 (nhận).

Có y(−5) = −50; y(−2) = 4; y(−1) = 2.

Vậy $\underset{\left[-5;-1\right]}{\min }y=y\left(-5\right)=-50$ .

Trắc nghiệm: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

I. Nhận biết

Câu 1. Cho hàm số $f\left(x\right)$ có đồ thị như hình bên. Giá trị lớn nhất của hàm số $f\left(x\right)$ trên đoạn đạt tại x bằng

A. 4.

B. 2

C. -3

D. 0.

Câu 2. Cho hàm số $f\left(x\right)$ xác định, liên tục trên $ℝ$ và có bảng biến thiên sau:

Giá trị nhỏ nhất của hàm số bằng :

A. -1

B. 3.

C. $\frac{1}{3}$.

D. 1.

Câu 3.Cho hàm số $y=f\left(x\right)$liên tục trên đoạn và có đồ thị trên đoạn như sau:

Tìm giá trị lớn nhất của hàm số $f\left(x\right)$trên đoạn .

Câu 4.Cho hàm số $f\left(x\right)$ có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?

A. Hàm số có GTNN bằng 0.

B. Hàm số không có GTLN và GTNN.

C. Hàm số có GTLN và không có GTNN.

D. Hàm số có GTLN bằng 3.

Câu 5.Cho hàm số $f\left(x\right)$ liên tục trên đoạn và có bảng biến thiên như sau

Giá trị lớn nhất của hàm số $f\left(x\right)$ liên tục trên đoạn bằng

A. $f\left(-1\right)$.

B. $f\left(3\right)$.

C. $f\left(2\right)$.

D. $f\left(0\right)$.

II. Thông hiểu

Câu 6. Cho hàm số y = f(x) liên tục trên đoạn và có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn . Giá trị của $M-m$bằng

A.6

B. 2.

C. 8.

D. 4.

Câu 7. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y=x^4-8x^2+3$ trên đoạn

A. $M=-3;m=-13$

B. $M=3;m=-4$

C.$M=-3;m=-4$

D. $M=3;m=-13$

Câu 8. Giá trị lớn nhất và nhỏ nhất của hàm số $y=x^3-12x+1$ trên đoạn lần lượt là :

A. $-15;17$.

B. $17;-15$.

C. $10;-26$.

D. $6;-26$

Câu 9.Tìm giá trị lớn nhất của hàm số $f\left(x\right)=\frac{x-2}{x+1}$ trên đoạn

A. Không tồn tại.

B. 0.

C. 2

D. -2

III. Vận dụng

Câu 10.Cho hàm số $y=\frac{x+m}{x-2}$thỏa mãn $\underset{\left(3;5\right)}{\min }y=4$. Mệnh đề nào dưới đây đúng

A.$m>5$.

B.$4\le m\le 5$

C.$2\le m<4$.

D.$m<2$.

Xem thêm tóm tắt lý thuyết Toán 12 sách Kết nối tri thức, chi tiết khác:

Lý thuyết Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Lý thuyết Bài 3: Đường tiệm cận của đồ thị hàm số

Lý thuyết Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Lý thuyết Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Lý thuyết Bài 6: Vectơ trong không gian

Xem thêm tài liệu Toán lớp 12:

Giải Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Giải SBT Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Giáo án Giá trị lớn nhất và giá trị nhỏ nhất của hàm số lớp 12

Giáo án điện tử Giá trị lớn nhất và giá trị nhỏ nhất của hàm số lớp 12