Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án
Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án
-
1106 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
08/10/2024Tam giác ABC có . Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
*Phương pháp giải:
- Áp dụng công thức tính diện tích tam giác theo sin/cos
*Lời giải:
Ta có: (đơn vị diện tích)
* Các dạng bài tập và lý thuyết thêm
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
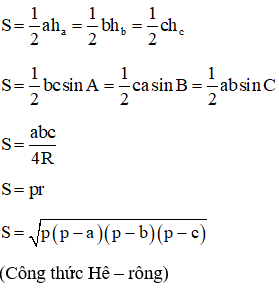
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Định lí côsin và định lí sin(có đáp án)
Câu 2:
06/12/2024Tam giác ABC có . Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
Ta có: .
Suy ra tam giác ABC cân tại A nên .
Diện tích tam giác ABC là (đơn vị diện tích)
*Phương pháp giải:
Áp dụng công thức tính diện tích tam giác
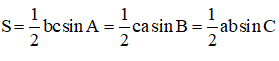
+ Phương pháp giải: Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
*Lý thuyết:
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
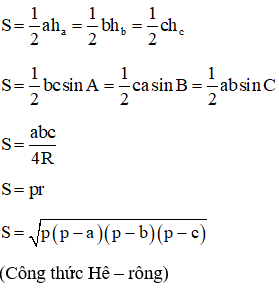
+ Phương pháp giải: Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
Xem thêm
Các công thức tính diện tích tam giác (2024) đầy đủ, chi tiết nhất
Câu 3:
23/07/2024Tam giác ABC có a = 21, b = 17, c = 10 .Diện tích của tam giác ABC bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:
Nửa chu vi của tam giác ABC là:
(đơn vị độ dài).
Do đó
Diện tích tam giác ABC là:
(đơn vị diện tích).
Câu 4:
23/07/2024Tam giác ABC có . Tính độ dài đường cao h kẻ từ đỉnh A xuống cạnh BC của tam giác.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
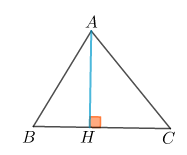
Áp dụng định lý hàm số cosin, ta có:
(đơn vị độ dài).
Ta có: (đơn vị diện tích).
Lại có (đơn vị độ dài).
Câu 5:
12/11/2024Tam giác ABC có . Tính độ dài đường cao h xuất phát từ đỉnh A của tam giác.
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải:
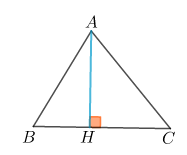
Gọi H là chân đường cao xuất phát từ đỉnh A.
Xét tam giác vuông AHC:
(đơn vị độ dài)
*Phương pháp giải:
- Xét tam giác vuông biết độ dài cạnh huyền và góc nhọn. Áp dụng tỉ số lượng giác sin cos vào tam giác vuông tìm ra đường cao AH:
sin C = AH / AC
*Công thức về giải tam giác - tính diện tích tam giác:
Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.
Công thức tính tdiện tích tam giác:
Cho tam giác ABC có BC = a, CA = b và AB = c, gọi ha, hb, hc là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB; R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác;
• Công thức Heron:
Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:
Cho tam giác ABC có BC = a, CA = b, AB = c, . Khi đó, diện tích S của tam giác ABC là:
.
Trong đó p là nửa chu vi tam giác ABC.
Công thức tính độ dài đường trung tuyến
Cho tam giác ABC vuông tại A, M là trung điểm của BC ta có: .
Gọi là độ dài đường trung tuyến lần lượt vẽ từ đỉnh A, B, C của tam giác ABC, ta có:
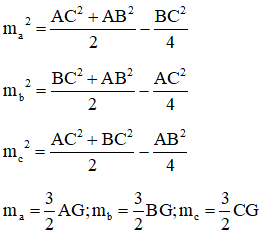
(với G là trọng tâm của tam giác ABC).
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giải tam giác. Tính diện tích tam giác – Toán 10 Cánh diều
Giải Toán 10 Bài 2 (Cánh diều): Giải tam giác. Tính diện tích tam giác
Câu 6:
22/07/2024Tam giác ABC có a = 21, b = 17, c = 10 . Gọi B’ là hình chiếu vuông góc của B trên cạnh AC. Tính BB’.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C

Ta có:
Nửa chu vi là:
(đơn vị độ dài).
Suy ra (đơn vị diện tích).
Lại có (đơn vị độ dài).
Câu 7:
20/07/2024Tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng . Giá trị sinA bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:
Câu 8:
22/07/2024Hình bình hành ABCD có và . Khi đó hình bình hành có diện tích bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
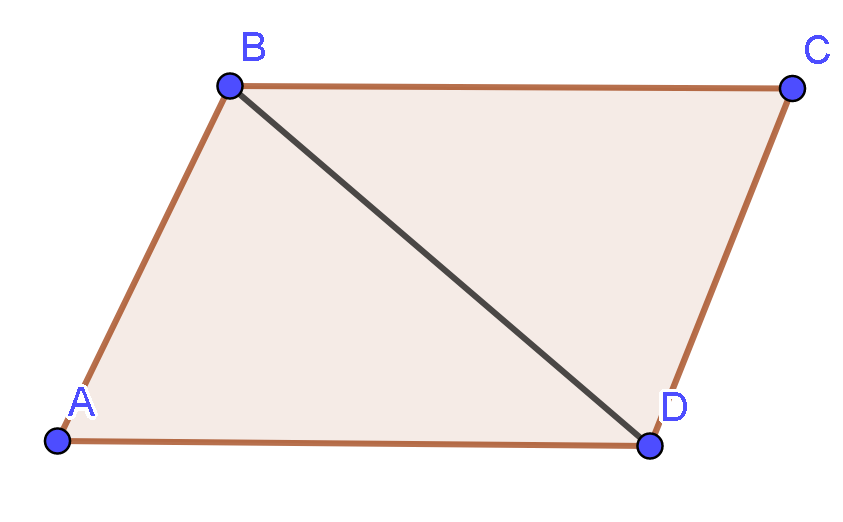
Diện tích tam giác ABD là: (đơn vị diện tích).(BC = AD = a)
Vậy diện tích hình bình hành ABCD là (đơn vị diện tích)
Câu 9:
22/07/2024Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
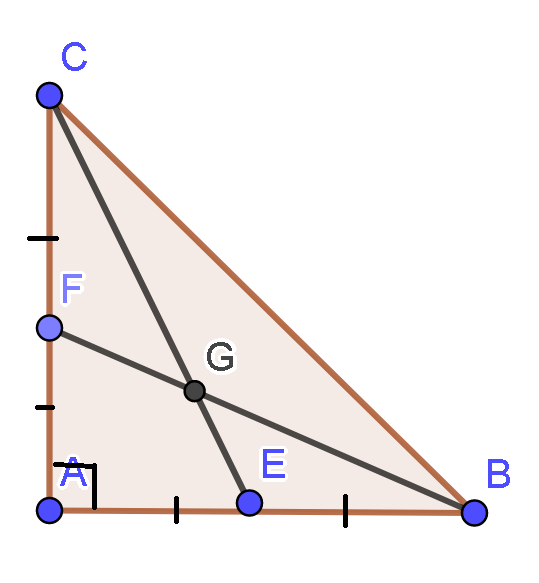
Vì F là trung điểm của AC
Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC.
Khi đó:
Vậy diện tích tam giác GFC là:
Câu 10:
23/07/2024Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét tam giác ABC đều, có độ dài cạnh bằng a.

Theo định lí sin, ta có: (đơn vị độ dài).
Vậy diện tích cần tính là:
Câu 11:
12/07/2024Tam giác ABC có và độ dài đường cao AH = 2. Tính độ dài cạnh AB.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Nửa chu vi là:
Ta có: .
Suy ra .
Lại có (đơn vị diện tích).
Từ đó ta có:
Câu 12:
18/07/2024Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Diện tích tam giác ABC ban đầu là:
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là:
Câu 13:
19/07/2024Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Diện tích tam giác ABC là:
Vì a, b dương và nên suy ra
Dấu xảy ra khi và chỉ khi
Vậy giá trị lớn nhất của diện tích tam giác ABC là (đơn vị diện tích).
Câu 14:
22/07/2024Tam giác cân có cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Giả sử tam ABC cân taị C, ta có: AC = BC = a; =
Diện tích tam giác là: S = a.b.sinC = .a.a.sin= sin.
Câu 15:
13/07/2024Tam giác ABC có . Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: = 4,5 (đơn vị diện tích).
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án (1105 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2) (636 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 Cánh diều Bài 1. Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác có đáp án (phần 2) (548 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 5. Tích Của Một Số Với Một Vectơ có đáp án (Phần 2) (541 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 6. Tích vô hướng của hai vectơ có đáp án (Phần 2) (516 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 4. Tổng và hiệu của hai vectơ có đáp án (Phần 2) (481 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2) (466 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 3. Vectơ có đáp án (Phần 2) (456 lượt thi)
- Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0 độ đến 180 độ . Định lý cosin và sin trong tam giác có đáp án (403 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Khái niệm vectơ có đáp án (347 lượt thi)
- Trắc nghiệm Toán 10 Bài 4. Tổng và hiệu hai vectơ có đáp án (334 lượt thi)
- Trắc nghiệm Toán 10 Bài 5. Tích của một số với một vectơ có đáp án (321 lượt thi)

