Câu hỏi:
06/12/2024 373
Tam giác ABC có . Tính diện tích tam giác ABC.
Tam giác ABC có . Tính diện tích tam giác ABC.
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Lời giải
Ta có: .
Suy ra tam giác ABC cân tại A nên .
Diện tích tam giác ABC là (đơn vị diện tích)
*Phương pháp giải:
Áp dụng công thức tính diện tích tam giác
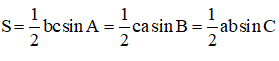
+ Phương pháp giải: Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
*Lý thuyết:
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
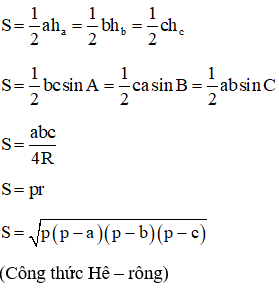
+ Phương pháp giải: Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
Xem thêm
Các công thức tính diện tích tam giác (2024) đầy đủ, chi tiết nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tam giác ABC có a = 21, b = 17, c = 10 .Diện tích của tam giác ABC bằng:
Tam giác ABC có a = 21, b = 17, c = 10 .Diện tích của tam giác ABC bằng:
Câu 2:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
Câu 3:
Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:
Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:
Câu 5:
Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
Câu 6:
Hình bình hành ABCD có và . Khi đó hình bình hành có diện tích bằng:
Hình bình hành ABCD có và . Khi đó hình bình hành có diện tích bằng:
Câu 7:
Tam giác ABC có a = 21, b = 17, c = 10 . Gọi B’ là hình chiếu vuông góc của B trên cạnh AC. Tính BB’.
Tam giác ABC có a = 21, b = 17, c = 10 . Gọi B’ là hình chiếu vuông góc của B trên cạnh AC. Tính BB’.
Câu 8:
Tam giác ABC có . Tính độ dài đường cao h xuất phát từ đỉnh A của tam giác.
Tam giác ABC có . Tính độ dài đường cao h xuất phát từ đỉnh A của tam giác.
Câu 9:
Tam giác ABC có . Tính độ dài đường cao h kẻ từ đỉnh A xuống cạnh BC của tam giác.
Tam giác ABC có . Tính độ dài đường cao h kẻ từ đỉnh A xuống cạnh BC của tam giác.
Câu 10:
Tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng . Giá trị sinA bằng:
Tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng . Giá trị sinA bằng:
Câu 11:
Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:
Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:
Câu 12:
Tam giác cân có cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là
Tam giác cân có cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là
Câu 13:
Tam giác ABC có và độ dài đường cao AH = 2. Tính độ dài cạnh AB.
Tam giác ABC có và độ dài đường cao AH = 2. Tính độ dài cạnh AB.


