Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác (có đáp án)
Trắc nghiệm Toán 7 Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác
-
347 lượt thi
-
24 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
18/07/2024Cho tam giác ABC có và độ dài cạnh AB là một số nguyên (cm). Tam giác ABC là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Gọi độ dài cạnh AB là x (x > 0).
Theo bất đẳng thức tam giác ta có:
Vì x là số nguyên nên . Độ dài cạnh
Tam giác ABC có nên tam giác ABC cân tại A
Câu 2:
20/07/2024Cho có M là trung điểm BC. So sánh với
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
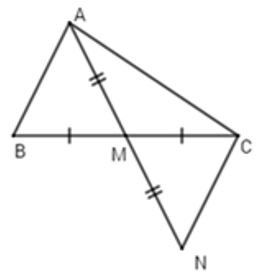
Trên tia đối của tia MA lấy điểm N sao cho
Vì M là trung điểm BC(gt) (tính chất trung điểm)
Xét và có:
MB = MC (cmt)
AM = MN (gt)
(đối đỉnh)
(1) (2 cạnh tương ứng)
Xét có: (2) (bất đẳng thức tam giác)
Từ (1) (2)
Mặt khác,
Câu 3:
23/07/2024Cho , em hãy chọn đáp án sai trong các đáp án sau:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án A, B, C đều đúng, đáp án D sai.
Câu 4:
21/07/2024Cho , trên BC lấy điểm M bất kì nằm giữa B và C. So sánh và
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
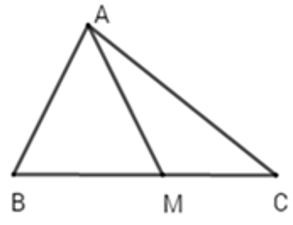
Xét có: (bất đẳng thức tam giác)
Xét có: (bất đẳng thức tam giác)
Vì M nằm giữa B và C (gt)
Cộng theo từng vế của hai bất đẳng thức trên ta được:
Câu 5:
22/07/2024Cho tam giác ABC có ; và độ dài cạnh AB là một số nguyên (cm). Tam giác ABC là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Gọi độ dài cạnh AB là x (x > 0).
Theo bất đẳng thức tam giác ta có:
Vì x là số nguyên nên . Độ dài cạnh
Tam giác ABC có nên tam giác ABC cân tại B
Câu 6:
22/07/2024Cho có điểm O là một điểm bất kì nằm trong tam giác. So sánh và
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
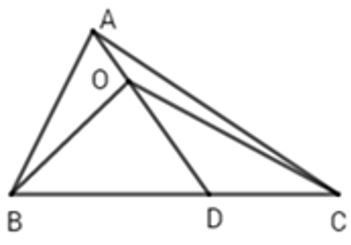
Gọi giao điểm của AO và BC là D. Do O nằm trong nên D nằm giữa B và C
Xét có: (bất đẳng thức tam giác)
Xét có: (bất đẳng thức tam giác)
Cộng vế với vế của (1) và (2) ta được:
Từ (*) và (**) ta có
Câu 7:
21/07/2024Có bao nhiêu tam giác có độ dài hai cạnh là 7 cm và 2 cm còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Gọi độ dài cạnh còn lại là
Theo bất đẳng thức tam giác ta có:
Vì x là số nguyên nên
Vì có ba giá trị của x thỏa mãn nên có ba tam giác thỏa mãn điều kiện đề bài
Câu 8:
21/07/2024Cho tam giác ABC có . Điểm M là trung điểm của BC. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
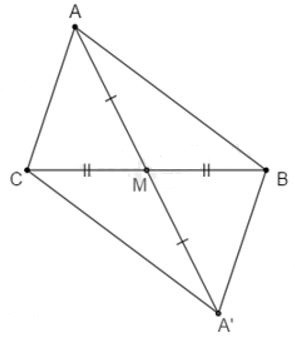
Trên tia đối của tia MA ta lấy điểm A' sao cho
Xét và có:
AM = A'M (cách vẽ)
MB = MC (vì M là trung điểm BC)
(đối đỉnh)
(hai cạnh tương ứng)
Xét có: (bất đẳng thức tam giác)
Mà (cmt); (theo cách vẽ) nên ta có:
Câu 9:
22/07/2024Cho , em hãy chọn đáp án đúng nhất trong các đáp án sau:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án B, C đều đúng.
Câu 10:
23/07/2024Cho có . Trên đường phân giác AD lấy điểm E. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
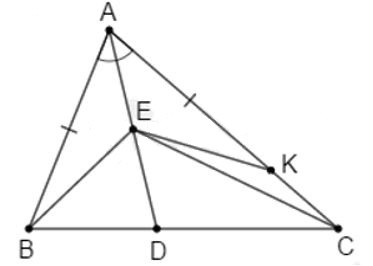
Trên cạnh AC lấy điểm K sao cho
Xét và có:
AE chung
AB = AK (cách dựng)
(vì AD là tia phân giác )
(hai cạnh tương ứng)
Áp dụng bất đẳng thức tam giác vào ta có: mà (cmt) suy ra (1)
Mặt khác (vì theo cách dựng) (2)
Từ (1) và (2) suy ra
Câu 11:
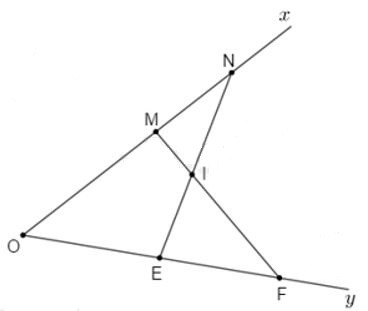
20/07/2024Cho hình vẽ dưới đây với là góc nhọn. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Áp dụng bất đẳng thức tam giác vào ta có:
(1)
Áp dụng bất đẳng thức tam giác vào ta có:
(2)
Cộng (1) với (2) theo vế với vế ta được:
Câu 12:
20/07/2024Có bao nhiêu tam giác có độ dài hai cạnh là 9 cm và 3 cm còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Gọi độ dài cạnh còn lại là
Theo bất đẳng thức tam giác ta có:
Vì x là số nguyên nên
Vì có năm giá trị của x thỏa mãn nên có năm tam giác thỏa mãn điều kiện đề bài
Câu 13:
18/07/2024Chọn câu đúng. Trong một tam giác:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Gọi độ dài ba cạnh của tam giác là a, b, c.
Nửa chu vi tam giác là
Ta có:
Tương tự ta cũng có ;
Câu 14:
22/07/2024Cho có cạnh và cạnh . Tính độ dài cạnh AC biết AC là một số nguyên tố lớn hơn 11
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Gọi độ dài cạnh AC là x (x > 0).
Theo bất đẳng thức tam giác ta có:
Vì x là một số nguyên tố lớn hơn 11 nên x = 13.
Vậy độ dài cạnh
Câu 15:
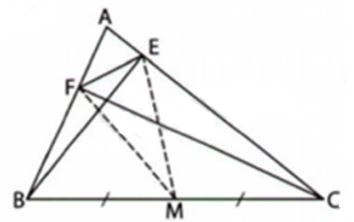
22/07/2024Cho tam giác ABC có hai đường vuông góc BE, CF. So sánh EF và BC
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
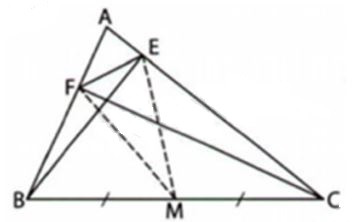
Gọi M là trung điểm của BC
Xét vuông tại E, M là trung điểm BC nên
Xét vuông tại F, M là trung điểm BC nên
Do đó:
Ba điểm M, E, F nằm trên cạnh của tam giác ABC nên không thể thẳng hàng do đó ba điểm M, E, F tạo thành một tam giác
Xét có: (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra
Câu 16:
18/07/2024Cho hình vẽ dưới đây. Chọn câu đúng
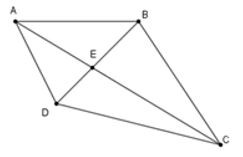
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Xét tam giác AED có (1) (quan hệ giữa ba cạnh của một tam giác)
Xét tam giác ECD có (2) (quan hệ giữa ba cạnh của một tam giác)
Xét tam giác EBC có: (3) (quan hệ giữa ba cạnh của một tam giác)
Xét tam giác ABE có (4) (quan hệ giữa ba cạnh của một tam giác)
Từ (1)(2)(3)(4) ta có:
![]()
Mà ; nên
Câu 17:
21/07/2024Cho có cạnh và cạnh . Tính độ dài cạnh AC biết AC là một số nguyên
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Gọi độ dài cạnh AC là x (x > 0). Theo bất đẳng thức tam giác ta có:
Vì x là số nguyên nên x = 4.
Vậy độ dài cạnh
Câu 18:
20/07/2024Cho tam giác ABC điểm M nằm trong tam giác. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
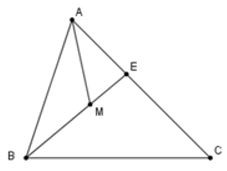
Kéo dài BM cắt AC tại E
Xét tam giác BEC có và xét tam giác AME có
(quan hệ giữa các cạnh trong tam giác)
Suy ra mà
Vậy MA + MB < AC +BC
Câu 19:
18/07/2024Dựa vào bất đẳng thứ tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
+ Xét bộ ba: 3cm; 5cm; 7cm. Ta có: (thỏa mãn bất đẳng thức tam giác nên bộ ba 3cm; 5cm; 7cm lập thành một tam giác. Loại A
+ Xét bộ ba: 4cm; 5cm; 6cm. Ta có: (thỏa mãn bất đẳng thức tam giác nên bộ ba 4cm; 5cm; 6cm lập thành một tam giác. Loại B
+ Xét bộ ba: 2cm; 5cm; 7cm. Ta có: (không thỏa mãn bất đẳng thức tam giác nên bộ ba 2cm; 5cm; 7cm không lập thành một tam giác. Chọn C
+ Xét bộ ba: 3cm; 5cm; 6cm. Ta có: (thỏa mãn bất đẳng thức tam giác nên bộ ba 3cm; 5cm; 6cm lập thành một tam giác. Loại D
Câu 20:
20/07/2024Cho cân tại A có một cạnh bằng 5cm. Tính cạnh BC của tam giác đó biết chu vi tam giác bằng 17cm
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
cân tại A
Trường hợp 1:
Ta có:
(thỏa mãn bất đẳng thức tam giác)
Trường hợp 2:
Ta có:
(thỏa mãn bất đẳng thức tam giác)
Vậy nếu cân tại A có:
Vậy BC = 5cm hoặc BC = 7cm
Câu 21:
20/07/2024Cho tam giác ABC biết ; và cạnh AC là một số tự nhiên lẻ. Chu vi ABC là
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Gọi độ dài cạnh AC là x (x > 0).
Theo bất đẳng thức tam giác ta có:
Vì x là số tự nhiên lẻ nên .
Độ dài cạnh
Chu vi tam giác ABC là:
Câu 22:
22/07/2024Cho cân tại A có một cạnh bằng 6cm. Tính cạnh BC của tam giác đó biết chu vi tam giác bằng 20cm
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
cân tại A
Trường hợp 1:
Ta có:
(thỏa mãn bất đẳng thức tam giác)
Trường hợp 2:
Ta có:
(thỏa mãn bất đẳng thức tam giác)
Vậy nếu cân tại A có:
Vậy BC = 8cm hoặc BC = 6cm
Câu 23:
21/07/2024Dựa vào bất đẳng thứ tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
+ Xét bộ ba: 6cm; 6cm; 5cm. Ta có: (thỏa mãn bất đẳng thức tam giác nên bộ ba 6cm; 6cm; 5cm lập thành một tam giác. Loại A
+ Xét bộ ba: 7cm; 8cm; 10cm. Ta có: (thỏa mãn bất đẳng thức tam giác nên bộ ba 7cm; 8cm; 10cm lập thành một tam giác. Loại B
+ Xét bộ ba: 12cm; 15cm; 9cm. Ta có: (thỏa mãn bất đẳng thức tam giác nên bộ ba 12cm; 15cm; 9cm lập thành một tam giác. Loại C
+ Xét bộ ba: 11cm; 20cm; 9cm. Ta có: (không thỏa mãn bất đẳng thức tam giác nên bộ ba 11cm; 20cm; 9cm không lập thành một tam giác.
Câu 24:
20/07/2024Cho tam giác ABC biết ; và cạnh AC là một số nguyên. Chu vi ABC là
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Gọi độ dài cạnh AC là x (x > 0).
Theo bất đẳng thức tam giác ta có:
Vì x là số nguyên nên .
Độ dài cạnh
Chu vi tam giác ABC là:
Có thể bạn quan tâm
- Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác (có đáp án) (346 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Tính chất ba đường trung trực của tam giác (có đáp án) (518 lượt thi)
- Trắc nghiệm Tính chất đường trung trực của một đoạn thẳng (có đáp án) (355 lượt thi)
- Trắc nghiệm Tính chất ba đường cao của tam giác (có đáp án) (355 lượt thi)
- Trắc nghiệm Quan hệ giữa góc và cạnh đối diện trong tam giác (có đáp án) (351 lượt thi)
- Trắc nghiệm Tính chất ba đường trung tuyến trong tam giác (có đáp án) (336 lượt thi)
- Trắc nghiệm Tính chất ba đường phân giác của tam giác (có đáp án) (334 lượt thi)
- Trắc nghiệm Tính chất tia phân giác của một góc (có đáp án) (327 lượt thi)
- Trắc nghiệm Quan hệ giữa đường vuông góc và đường xiên. Đường xiên và hình chiếu của đường xiên (có đáp án) (311 lượt thi)
- Trắc nghiệm ôn tập chương 3 (có đáp án) (271 lượt thi)
