17 câu hỏi trắc nghiệm thuộc Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Phần 2)

Câu 1:

18/07/2024

Nghiệm của phương trình sinx=1 là:

A. $x = - \frac{π}{2} + k 2 π$

B. $x = \frac{π}{2} + k π$

C. $x = k π$

D. $x = \frac{π}{2} + k 2 π$

Xem đáp án

Câu 2:

23/07/2024

Chọn mệnh đề sai:

A. $\sin x = - 1 \Leftrightarrow x = - \frac{π}{2} + k 2 π (k \in Z)$

B. $\sin x = 0 \Leftrightarrow x = k π (k \in Z)$

C. $\sin x = 0 \Leftrightarrow x = k 2 π (k \in Z)$

D. $\sin x = 1 \Leftrightarrow x = \frac{π}{2} + k 2 π (k \in Z)$

Xem đáp án

Câu 3:

22/07/2024

Nghiệm của phương trình cosx=1 là:

A. $x = k π$

B. $x = \frac{π}{2} + k 2 π$

C. $x = k 2 π$

D. $x = \frac{π}{2} + k π$

Xem đáp án

Câu 4:

23/07/2024

Phương trình cos2x=1 có nghiệm là:

A. $x = k π (k \in Z)$

B. $x = \frac{π}{2} + k 2 π (k \in Z)$

C. $x = k 2 π (k \in Z)$

D. $x = \frac{π}{2} + k π (k \in Z)$

Xem đáp án

Câu 5:

27/11/2024

Chọn mệnh đề đúng:

A. $\cos x \neq 1 \Leftrightarrow x \neq \frac{π}{2} + k π (k \in Z)$

B. $\cos x \neq 0 \Leftrightarrow x \neq \frac{π}{2} + k π (k \in Z)$

C. $\cos x \neq - 1 \Leftrightarrow x \neq - \frac{π}{2} + k 2 π (k \in Z)$

D. $\cos x \neq 0 \Leftrightarrow x \neq \frac{π}{2} + k 2 π (k \in Z)$

Xem đáp án

Đáp án đúng: B

* Lời giải:

*Phương pháp giải:

- sử dụng các phép biến đổi lượng giác để biến đổi phép tính đưa ra kết quả

*Lý thuyết và các dạng bài tập về phép biến đổi lượng giác:

Công thức cộng

$\begin{array}{l} \sin (a + b) = \sin a \cos b + \cos a s i n b \\ s i n (a - b) = \sin a \cos b - \cos a s i n b \\ \cos (a + b) = \cos a \cos b - \sin a s i n b \\ \cos (a - b) = \cos a \cos b + \sin a s i n b \\ \tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a \tan b} \\ \tan (a - b) = \frac{\tan a - \tan b}{1 + \tan a \tan b} \end{array}$

Công thức nhân đôi

$\begin{array}{l} \sin 2 a = 2 \sin a \cos a \\ \cos 2 a = \cos^{2} a - \sin^{2} a = 2 \cos^{2} a - 1 = 1 - 2 \sin^{2} a \\ \tan 2 a = \frac{2 \tan a}{1 - \tan^{2} a} \end{array}$

Suy ra, công thức hạ bậc:

$\sin^{2} a = \frac{1 - \cos 2 a}{2}, \cos^{2} a = \frac{1 + \cos 2 a}{2}$

Công thức biến đổi tích thành tổng

$\begin{array}{l} \cos a \cos b = \frac{1}{2} [\cos (a + b) + \cos (a - b)] \\ \sin a \sin b = \frac{1}{2} [\cos (a - b) - \cos (a + b)] \\ \sin a \cos b = \frac{1}{2} [\sin (a + b) + \sin (a - b)] \end{array}$

Công thức biến đổi tổng thành tích

$\begin{array}{l} \cos a + \cos b = 2 \cos \frac{a + b}{2} \cos \frac{a - b}{2} \\ \cos a - \cos b = - 2 \sin \frac{a + b}{2} \sin \frac{a - b}{2} \\ \sin a + \sin b = 2 \sin \frac{a + b}{2} \cos \frac{a - b}{2} \\ \sin a - \sin b = 2 \cos \frac{a + b}{2} \sin \frac{a - b}{2} \end{array}$

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Các phép biến đổi lượng giác – Toán 11 Cánh diều

Sách bài tập Toán 11 Bài 2 (Cánh diều): Các phép biến đổi lượng giác

Trắc nghiệm Các phép biến đổi lượng giác (Cánh diều) có đáp án - Toán 11

Câu 6:

22/07/2024

Nghiệm của phương trình cosx=-1 là:

A. $x = π + k π$

B. $x = - \frac{π}{2} + k 2 π$

C. $x = π + k 2 π$

D. $x = \frac{3 π}{2} + k π$

Xem đáp án

Câu 7:

18/07/2024

Nghiệm của phương trình $\cos x = - \frac{1}{2}$ là:

A. $x = \pm \frac{π}{3} + k 2 π$

B. $x = \pm \frac{π}{6} + k 2 π$

C. $x = \pm \frac{2 π}{3} + k 2 π$

D. $x = \pm \frac{π}{6} + k π$

Xem đáp án

Câu 8:

18/07/2024

Nghiệm của phương trình $\sqrt{3} \tan x + 3 = 0$ là:

A. $x = \frac{π}{3} + k π (k \in Z)$

B. $x = - \frac{π}{3} + k 2 π (k \in Z)$

C. $x = \frac{π}{6} + k π (k \in Z)$

D. $x = - \frac{π}{3} + k π (k \in Z)$

Xem đáp án

Câu 9:

18/07/2024

Phương trình $\tan \frac{x}{2} = \tan x$ có nghiệm

A. $k 2 π (k \in Z)$

B. $k π (k \in Z)$

C. $π + k 2 π (k \in Z)$

D. Cả 3 đáp án đúng

Xem đáp án

Câu 10:

18/07/2024

Tìm số nghiệm trong khoảng $(- π; π)$ của phương trình sinx=cos2x

A. 3

B. 2

C. 1

D. 4

Xem đáp án

Câu 11:

22/12/2024

Số nghiệm của phương trình $\sqrt{2} \cos (x + \frac{π}{3}) = 1$ với $0 \leq x \leq 2 π$ là:

A. 0

B. 2

C. 1

D. 3

Xem đáp án

Đáp án đúng là B

Lời giải

*Phương pháp giải:

Sử dụng công thức lượng giác đặc biệt rồi xét với điều kiện đề bài cho

*Lý thuyết:

1. Phương trình sinx = a.

Xét phương trình sinx = a (1)

- Trường hợp |a| > 1

Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.

- Trường hợp |a| ≤ 1

Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:

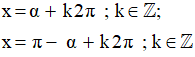
Nếu số thực α thỏa mãn điều kiện: $\{\begin{matrix} \frac{- π}{2} \leq α \leq \frac{π}{2} \\ \sin α = a \end{matrix}$ thì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:

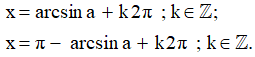
- Chú ý:

a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

$x = α + k 2 π$ và $x = π - α + k 2 π; k \in ℤ$

Tổng quát:

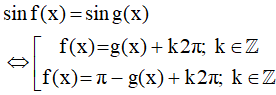
b) Phương trình sinx = sinβ⁰ có các nghiệm là:

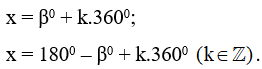
c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là $x = \frac{π}{2} + k 2 π; k \in ℤ$ .

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là $x = - \frac{π}{2} + k 2 π; k \in ℤ$ .

+ Khi a = 0: Phương trình sinx = 0 có các nghiệm là $x = k π; k \in ℤ$ .

2. Phương trình cosx = a.

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $|cosx| \leq 1$ với mọi x.

- Trường hợp $|a| \leq 1$ .

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x = \pm α + k 2 π; k \in ℤ$

- Chú ý:

a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là: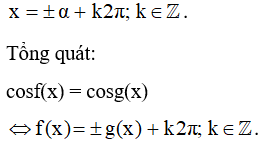

b) Phương trình cos x= cosβ⁰ có các nghiệm là $x = \pm β^{0} + k 360^{0}; k \in ℤ$

c) Nếu số thực α thỏa mãn điều kiện: $\{\begin{matrix} 0 \leq α \leq π \\ \cos α = a \end{matrix}$ thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là: