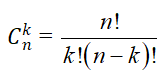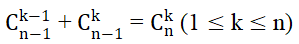30 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Bài 2: Hoán vị - Chỉnh hợp

Lý thuyết Phép cộng, phép trừ các số tự nhiên chi tiết – Toán lớp 6 Cánh diều

Cho $A = \{a; b; c\}$ . Số hoán vị của ba phần tử của A là:

A. 4

B. 5

C. 6

D. 7

Xem đáp án

Chọn đáp án C

Số hoán vị của ba phần tử của A là 3! = 6.

Câu 2:

20/11/2024

Một lớp học có 30 học sinh, trong đó có 18 em giỏi Toán, 14 em giỏi văn và 10 em không giỏi môn nào. Số tất cả các em giỏi cả văn lẫn toán là:

A. 20

B. 12

C. 24

D. 48

Xem đáp án

Chọn đáp án B

Lời giải

Số học sinh giỏi ít nhất 1 môn là:

30 – 10 = 20

Số học sinh giỏi cả văn lẫn toán là:

18 + 14 – 20 = 12.

*Phương pháp giải:

Tính số học sinh giỏi chỉ 1 môn

Tính số học sinh giỏi cả 2 môn

*Lý thuyết

1. Phép cộng hai số tự nhiên

a + b = c

(số hạng) + (số hạng) = (tổng)

Ví dụ: 3 + 2 = 5; 10 + 24 = 34

2. Tính chất của phép cộng các số tự nhiên

+ Phép cộng các số tự nhiên có các tính chất: giao hoán, kết hợp, cộng với số 0.

Tính chất	Phát biểu	Kí hiệu
Giao hoán	Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.	a + b = b + a
Kết hợp	Muốn cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.	(a + b) + c = a + (b + c)
Cộng với số 0	Bất kì số nào cộng với số 0 cũng bằng chính nó.	a + 0 = 0 + a = a

+ Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a + b + c có thể được tính theo một trong hai cách sau: a + b + c = (a + b) + c hoặc a + b + c = a + (b + c).

Ví dụ: Tính: 65 + 97 + 35

Lời giải:

65 + 97 + 35

= 65 + 35 + 97 (tính chất giao hoán)

= (65 + 35) + 97 (tính chất kết hợp)

= 100 + 97

= 197

II. Phép trừ

1. Phép trừ hai số tự nhiên

a – b = c (a $\geq$ b)

(số bị trừ) – (số trừ) = (hiệu)

Ví dụ: 12 – 7 = 5; 23 – 3 = 20

2. Lưu ý

+ Nếu a – b = c thì a = b + c và b = a – c.

+ Nếu a + b = c thì a = c – b và b = c – a.

Xem thêm

TOP 40 câu Trắc nghiệm Phép cộng, phép trừ các số tự nhiên (Cánh diều 2024) có đáp án - Toán 6

Câu 3:

21/07/2024

Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:

A. 60

B. 180

C. 330

D. 90

Xem đáp án

Chọn đáp án A

Chọn 3 học sinh lớp 12 có $C_{4}^{3} . C_{3}^{1} . C_{5}^{1} = 60$ cách chọn.

Câu 4:

21/07/2024

Số hoán vị của n phần tử là:

A. $n^{2}$

B. $n^{n}$

C. $2 n$

D. $n!$

Xem đáp án

Chọn đáp án D

Số hoán vị của n phần tử là

Câu 5:

17/07/2024

Có bao nhiêu số có 4 chữ số khác nhau được tạo thành từ các số 1, 2, 3, 4, 5?

A. $P_{4}$

B. $P_{5}$

C. $A_{5}^{4}$

D. $C_{5}^{4}$

Xem đáp án

Chọn đáp án C

Số có 4 chữ số khác nhau tạo thành từ tập trên là $A_{5}^{4}$

Câu 6:

Cho $n, k \in ℕ$ với $0 < k \leq n$ . Mệnh đề nào có giá trị sai?

A.

B.

C.

D.

Xem đáp án

Chọn đáp án A

Ta có $P_{0} = 0$ nên A sai.

Câu 7:

19/07/2024

Từ 6 chữ số 0, 1, 2, 3, 4, 5 ta lập được bao nhiêu số chẵn, mỗi số gồm 5 chữ số khác nhau?

A. 120

B. 192

C. 312

D. 216

Xem đáp án

Chọn đáp án C

Giả sử số đó là

Trường hợp 1:

Trường hợp 2: $\Rightarrow$

Do đó có

Câu 8:

Có 18 đội bóng đá tham gia thi đấu. Mỗi đội chỉ có thể nhận nhiều nhất là một huy chương và đội nào cũng có thể đoạt huy chương. Khi đó, số cách trao 3 loại huy chương vàng, bạc, đồng cho ba đội nhất nhì ba là:

A. 51

B. 4896

C. 125

D. 12070

Xem đáp án

Chọn đáp án B

Ta có 3 đội bất kì trong 18 đội đều có khả năng đạt huy chương, và thứ tự của 3 đội này sẽ cho biết loại huy chương mà mỗi đội nhận, đo đó số cách trao cần tìm:

Câu 9:

Cho số $M = 2^{5} . 3^{3} . 5^{4}$ M có tất cả bao nhiêu ước số dương?

A. 60

B. 13

C. 140

D. 120

Xem đáp án

Chọn đáp án D

Số ước dương là:

Câu 10:

Có bao nhiêu số là ước dương của $2^{10} . 3^{6} . 5^{8}$ và chia hết cho $2^{5} . 3^{2} . 5^{4}$ ?

A. 30

B. 150

C. 60

D. 120

Xem đáp án

Chọn đáp án B

Để ý rằng

Với mỗi ước dương của $2^{5} . 3^{4} . 5^{4}$ khi nhân với $2^{10} . 3^{6} . 5^{8}$ đều là ước dương của thỏa mãn yêu cầu đề. Số ước dương cần tìm là: $(5 + 1) (4 + 1) (4 + 1) = 150$

Câu 11:

Trong một bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy được 2 viên cùng màu?

A. 18

B. 9

C. 22

D. 4

Xem đáp án

Chọn đáp án B

Số cách lấy hai viên bi cùng màu đỏ là $C_{4}^{2}$ cách.

Câu 12:

18/07/2024

Một tổ học sinh có 5 nam và 5 nữ xếp thành 1 hàng dọc sao cho không có học sinh cùng giới tính đứng kề nhau. Số cách xếp là:

A. 5!.5!

B. $2 . {(5!)}^{2}$

C. 10!

D. 2.5!

Xem đáp án

Chọn đáp án B

Theo bài ra, ta thấy cách sắp xếp chính là việc nam nữ đứng xen kẽ nhau.

Như vậy sẽ có hai trường hợp, hoặc là bạn nam đứng đầu hàng hoặc là bạn nữ đứng đầu hàng.

Và 5 bạn nam thay đổi vị trí cho nhau tương ứng với 5! cách.

Tương tự với 5 bạn nữ thay đổi vị trí tương ứng với 5! cách.

Vậy số cách sắp xếp cần tìm $2 . {(5!)}^{2}$

Câu 13:

Cho 5 chữ số 0, 1, 2, 3, 4. Có bao nhiêu số gồm 5 chữ số khác nhau được tạo thành từ 5 chữ số trên?

A. 120

B. 96

C. 24

D. 28

Xem đáp án

Chọn đáp án B

Câu 14:

Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau và chia hết cho 9?

A. 16

B. 18

C. 20

D. 14

Xem đáp án

Chọn đáp án A

Câu 15:

Cho 5 chữ số 1, 2, 3, 4, 5. Từ 5 chữ số này ta lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau?

A. 120

B. 60

C. 30

D. 40

Xem đáp án

Chọn đáp án A

Số có 5 chữ số khác nhau dc tạo thành từ tập trên là 5! = 120.

Câu 16:

21/07/2024

Một tổ học sinh có 5 nam và 5 nữ xếp thành một hàng dọc thì số các cách xếp khác nhau là:

A. 25

B. 10

C. 10!

D. 40

Xem đáp án

Chọn đáp án C

Số cách xếp là 10!.

Câu 17:

17/07/2024

Cho 5 chữ số 1, 2, 3, 4, 5. Từ 5 chữ số này, ta lập các số chẵn có 5 chữ số khác nhau. Số các số có thể lập được là:

A. 120

B. 48

C. 32

D. 40

Xem đáp án

Chọn đáp án B

Giả sử số đó là

Chọn $a_{5}$ có 2 cách,

Câu 18:

Dũng có 8 người bạn. Dũng muốn mời 4 trong 8 người bạn đó về quê chơi vào cuối tuần. Nhưng trong 8 người bạn đó, có 2 bạn là Hùng và Tuấn không thích đi chơi với nhau. Như vậy số cách chọn nhóm 4 người để về quê của Dũng là?

A.

B.

C.

D.

Xem đáp án

Chọn đáp án C

TH1. Trong 4 bạn được mời, có Hùng nhưng không có Tuấn.

$C_{6}^{3}$ cách.

TH3. Trong 4 bạn được mời, không có cả Hùng và Tuấn.

$\to_{}^{}$ Số cách chọn nhóm 4 người trong trường hợp này là $C_{6}^{4}$ $C_{6}^{4}$ cách.

Vậy số cách chọn cần tìm là

Câu 19:

Một tổ có 6 học sinh, trong đó có 3 học sinh nam và 3 học sinh nữ. Hỏi có bao nhiêu cách xếp các học sinh trong tổ thành một hàng dọc sao cho nam, nữ đứng xen kẽ nhau?

A. 36

B. 42

C. 102

D. 72

Xem đáp án

Chọn đáp án D

Ta xét hai trường hợp:

TH1. Bạn nam đứng đầu hàng, khi đó số cách sắp xếp là 3.2.3! = 36 cách.

TH2. Bạn nữ đứng đầu hàng, tương tự TH1, suy ra có 36 cách sắp xếp.

Vậy có 72 cách sắp xếp thỏa mãn yêu cầu bài toán.

Câu 20:

Hai đơn vị thi đấu cờ tướng A và B lần lượt có 5 người và 6 người. Cần chọn ra mỗi đơn vị 3 người để ghép cặp thi đấu với nhau. Hỏi có bao nhiêu cách thực hiện như thế?

A. 1200

B.

C.

D.

Xem đáp án

Chọn đáp án A

Số cách chọn 3 người từ đơn vị A là $C_{5}^{3}$ cách.

Số cách chọn 3 người từ đơn vị B là $C_{6}^{3}$ cách thực hiện việc ghép cặp thi đấu.

Câu 21:

Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Hỏi có bao nhiêu cách tuyển chọn?

A. 240

B. 260

C. 126

D. Kết quả khác

Xem đáp án

Chọn đáp án C

Số cách chọn ban quản trị gồm 1 nam và 3 nữ là $C_{5}^{1} . C_{4}^{3}$ cách.

Số cách chọn ban quản trị gồm 2 nam và 2 nữ là $C_{5}^{2} . C_{4}^{2}$ cách.

Số cách chọn ban quản trị gồm 3 nam và 1 nữ là $C_{5}^{3} . C_{4}^{1}$ cách.

Số cách chọn ban quản trị gồm 4 nam là $C_{5}^{4}$ cách.

Vậy tổng số cách chọn cần tìm là

Câu 22:

Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - Toán 10 Kết nối tri thức

Có bao nhiêu cách chọn và sắp thứ tự 5 cầu thủ để đá bóng luân lưu 11m. Biết rằng cả 11 cầu thủ đều có khả năng như nhau.

A. 55440

B. 20680

C. 32456

D. 41380

Xem đáp án

Chọn đáp án A

Số cách chọn 5 cầu thủ trong 11 cầu thủ và sắp xếp có thứ tự là

Câu 23:

17/07/2024

Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn?

A. 240

B. 260

C. 126

D. Kết quả khác

Xem đáp án

Chọn đáp án D

Số cách chọn ban quản trị gồm 1 nam và 3 nữ là $C_{5}^{1} . C_{4}^{3}$ cách.

Số cách chọn ban quản trị gồm 2 nam và 2 nữ là $C_{5}^{2} . C_{4}^{2}$ cách.

Vậy tổng số cách chọn cần tìm là

cách.

Câu 24:

20/11/2024

Một lớp có 50 học sinh. Hỏi có bao nhiêu cách phân công 3 học sinh để làm vệ sinh lớp học trong một ngày?

A. 117600

B. 128500

C. 376

D. 436

Xem đáp án

Chọn đáp án A

Lời giải

Số cách phân công 3 học sinh để làm vệ sinh lớp học là

*Phương pháp giải:

Sử dụng chỉnh hợp

*Lý thuyết:

Một chỉnh hợp chập k của n là một cách sắp xếp có thứ tự k phần tử từ một tập hợp n phần tử (với k, n là các số tự nhiên, 1 ≤ k ≤ n).

Số các chỉnh hợp chập k của n, kí hiệu là $A_{n}^{k}$ , được tính bằng công thức:

$A_{n}^{k}$ = n.(n – 1)…(n – k + 1) hay $A_{n}^{k} = \frac{n!}{(n - k)!}$ (1 ≤ k ≤ n).

Chú ý :

+ Hoán vị sắp xếp tất cả các phần tử của tập hợp, còn chỉnh hợp chọn ra một số phần tử và sắp xếp chúng.

+ Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó. Vì vậy P_n = $A_{n}^{n}$

Ví dụ: Một nhóm có 8 học sinh, giáo viên muốn chọn ra hai bạn, trong đó một bạn làm nhóm trưởng và một bạn làm nhóm phó. Hỏi có bao nhiêu cách chọn ?

Hướng dẫn giải

Mỗi cách chọn lần lượt 2 bạn trong 8 bạn, một bạn làm nhóm trưởng và một bạn làm nhóm phó là một chỉnh hợp chập 2 của 8 học sinh.

Ta có : $A_{8}^{2} = \frac{8!}{(8 - 2)!} = 56$

Vậy có 56 cách chọn ra 2 trong 8 bạn, một bạn làm nhóm trưởng, một bạn làm nhóm phó.

Xem thêm

TOP 40 câu Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp (có đáp án ) – Toán 11

Câu 25:

Có 3 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy?

A. 200

B. 30

C. 300

D. 120

Xem đáp án

Chọn đáp án D

Cố định 3 tem thư xếp theo hàng ngang từ trái sang phải là các vị trí 1, 2, 3.

Rõ ràng nếu có 3 bì thư thì mỗi thứ tự xếp 3 bì thư này từ trái sáng phải cũng chính là cách dán.

Số cách làm cần tìm là:

Câu 26:

Từ 12 người, người ta thành lập một ban kiểm tra gồm 2 người lãnh đạo và 3 ủy viên. Hỏi có bao nhiêu cách thành lập ban kiểm tra?

A.

B.

C.

D. Kết quả khác

Xem đáp án

Chọn đáp án A

Câu 27:

Có 4 cuốn sách toán khác nhau, 3 sách lý khác nhau, 2 sách hóa khác nhau. Muốn sắp và một kệ dài các cuốn sách cùng môn kề nhau, 2 loại toán và lý phải kề nhau thì số cách sắp là:

A. 4!.3!.2!

B. 2.4!.3!.2!

C. 3.4!.3!.2!

D. 4.4!.3!.2!

Xem đáp án

Chọn đáp án D

Đối với 3 vị trí của 3 loại sách thì sách hóa chỉ có thể đứng ở đầu hoặc cuối: 2 cách chọn.

Tương ứng mỗi vị trí của loại sách hóa thì số cách xếp các cuốn sách hóa là: 2!

Tương tự, số cách xếp toán và lý là: 2.4!.3!

Vậy tổng số cách xếp cần tìm: 2.4!.3!.(2!.2) = 4.4!.3!.2!.

Câu 28:

Từ các số 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số có 7 chữ số khác nhau mà hai chữ số chẵn đứng kề nhau?

A. 6!

B. 2.6!

C. 7!

D. 2.7!

Xem đáp án

Chọn đáp án B

Số số có 7 chữ số khác nhau lập từ các chữ số đã cho: 7!

Xếp 4 chữ số lẻ trên 1 hàng ngang với vị trí bất kì: 4! Cách.

Ở đây giữa sẽ tạo thành 5 khoảng trống (bao gồm 3 khoảng trống giữa hai chữ số lẻ và 2 khoảng trống tại vị trí đầu và cuối). Ở mỗi khoảng trống, ta sẽ điền các chữ số chẵn 2, 4, 6 vào không kể thứ tự sao cho mỗi khoảng trống chỉ có 1 chữ số chẵn: $A_{5}^{3}$

Cách xếp này cũng chính là số số thỏa yêu cầu đề: $A_{5}^{3} . 4! = 2.6!$

Câu 29:

Có 3 môn thi Toán, Lí, Hóa cần xếp vào 3 buổi thi, mỗi buổi 1 môn sao cho môn Toán không thi buổi đầu thì số cách xếp là:

A. 3!

B. 2!

C. 3! – 2!

D. 5

Xem đáp án

Chọn đáp án C

Số cách xếp bất kì 3 môn vào 3 buổi thi bất kì là: 3!

Giả sử môn Toán luôn thi buổi đầu, thì số cách xếp 2 môn còn lại vào bất kì 2 buổi còn lại là: 2!

Vậy số cách xếp cần tìm: 3! – 2!.

Câu 30: