27 câu hỏi trắc nghiệm thuộc Trắc nghiệm Chương 1: Hàm số lượng giác và phương trình lượng giác có đáp án (Đề số 2)

Hình nào sau đây là đồ thị hàm số y=|sinx|?

A.

B.

C.

D.

Xem đáp án

Câu 3:

Số vị trí biểu diễn các nghiệm của phương trình $\sin (2 x + \frac{π}{3}) = \frac{1}{2}$ trên đường tròn lượng giác là?

A. 1

B. 2

C. 4

D. 6

Xem đáp án

Câu 4:

19/07/2024

Với những giá trị nào của x thì giá trị của các hàm số y=sin3x và y=sinx bằng nhau?

A. $[\begin{matrix} x = k 2 π \\ x = \frac{π}{4} + k 2 π \end{matrix} (k \in Z)$

B. $[\begin{matrix} x = k π \\ x = \frac{π}{2} + \frac{kπ}{2} \end{matrix} (k \in Z)$

C. $x = k \frac{π}{4} (k \in Z)$

D. Đáp án khác

Xem đáp án

Câu 5:

Gọi $x_{0}$ là nghiệm dương nhỏ nhất của phương trình $\frac{2 \cos 2 x}{1 - \sin 2 x} = 0$ . Mệnh đề nào sau đây là đúng?

A. $x_{0} \in (0; \frac{π}{4})$

B. $x_{0} \in [\frac{π}{4}; \frac{π}{2}]$

C. $x_{0} \in (\frac{π}{2}; \frac{3 π}{4})$

D. $x_{0} \in [\frac{3 π}{4}; π]$

Xem đáp án

Câu 6:

Lý thuyết Phương trình lượng giác cơ bản

Hỏi trên đoạn [-2017;2017] phương trình $(\sin x + 1) (\sin x - \sqrt{2}) = 0$ có tất cả bao nhiêu nghiệm?

A. 4034

B. 4035

C. 641

D. 642

Xem đáp án

Câu 7:

18/10/2024

Tính tổng T các nghiệm của phương trình $\sin 2 x - \cos x = 0$ trên $[0; 2 π]$

A. $T = 3 π$

B. $T = \frac{5 π}{2}$

C. $T = 2 π$

D. $T = π$

Xem đáp án

Đáp án đúng là A

*Phương pháp giải

Công thức nghiệm cơ bản phương trình sin x = m

Trường hợp 1: |m| > 1. Phương trình vô nghiệm.

Trường hợp 2: |m| ≤ 1. Phương trình có nghiệm.

- Nếu m biểu diễn được dưới dạng sin của những góc đặc biệt thì:

sinx = m ⇔ sinx = sinα ⇔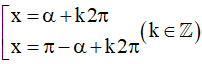

- Nếu m không biểu diễn được dưới dạng sin của những góc đặc biệt thì:

sinx = m ⇔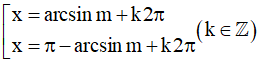

- Sử dụng công thức lượng giác hai góc phụ nhau: $\sin (\frac{π}{2} - x) = \cos x$

*Lời giải

Xem thêm các bài viết liên quan hay chi tiết:

Công thức biến đổi biểu thức asinx + bcosx

Câu 8:

08/11/2024

Giải phương trình $c o t (3 x - 1) = - \sqrt{3}$

A. $x = \frac{1}{3} + \frac{5 π}{18} + k \frac{π}{3} (k \in Z)$

B. $x = \frac{1}{3} + \frac{π}{18} + k \frac{π}{3} (k \in Z)$

C. $x = \frac{5 π}{18} + k \frac{π}{3} (k \in Z)$

D. $x = \frac{1}{3} - \frac{π}{18} + k \frac{π}{3} (k \in Z)$

Xem đáp án

Đáp án đúng: A

* Lời giải:

Ta có: - $\sqrt{3}$ = cot( $\frac{5 π}{6}$ )

nên: cot(3x - 1) = - $\sqrt{3}$

$\Leftrightarrow$ cot(3x - 1) = cot( $\frac{5 π}{6}$ )

$\Leftrightarrow$ 3x - 1 = $\frac{5 π}{6}$ + k $π$ ( k $\in$ Z)

$\Leftrightarrow$ 3x = 1 + $\frac{5 π}{6}$ + k $π$ ( k $\in$ Z)

$\Leftrightarrow$ x = $\frac{1}{3}$ + $\frac{5 π}{18}$ + $\frac{k π}{3}$ ( k $\in$ Z)

* Phương pháp giải:

- Lấy nghịch đảo cotang của hai vế của phương trình để trích xuất 3x-1 từ trong hàm cotang: 3x -1 = arccot( $- \sqrt{3}$ )

- Rút gọn vế phải : 3x - 1 = $\frac{5 π}{6}$

- Thực hiện chuyển vế đưa x về một vế và số về một vế : 3x = 1 + $\frac{5 π}{6}$

- Tính toán kết quả vế phải và chia cả 2 vế cho 3 để thu được kết quả của x: x = $\frac{1}{3} + \frac{5 π}{18}$

Do hàm cotang âm ở góc phần tư thứ 2 và 4 nên ta phải thêm $k π$ vào kết quả khi lấy nghịch đảo cotang ra

Vậy kết quả cuối cùng là: x = $\frac{1}{3} + \frac{5 π}{18} + k π (k \in Z)$

* Lý thuyết cần nắm và một số phương trình lượng giác thường gặp:

a) Phương trình bậc nhất đối với một hàm số lượng giác

*Phương pháp giải:

Chuyển vế rồi chia hai vế của phương trình dạng at+b=0 (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.

b) Phương trình bậc hai đối với một hàm số lượng giác

*Phương pháp giải:

Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này. Cuối cùng ta đưa về việc giải các phương trình lượng giác cơ bản.

1. Hàm số y = sinx.

Từ định nghĩa ta thấy hàm số y = sinx :

+ Xác định với mọi x $\in ℝ$ và – 1 ≤ sinx ≤ 1.

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì 2π.

Sau đây, ta sẽ khảo sát sự biến thiên của hàm số y = sinx.

a) Sự biến thiên và đồ thị hàm số y = sinx trên đoạn [0; π].

Hàm số y = sinx đồng biến trên $[0; \frac{π}{2}]$ và nghịch biến trên $[\frac{π}{2}; π]$ .

Bảng biến thiên:

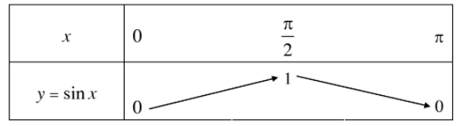
Đồ thị của hàm số y = sinx trên đoạn [0; π] đi qua các điểm (0; 0); (x1; sinx1); (x2; sinx2); (x3; sinx3); (x4; sinx4); (π; 0).

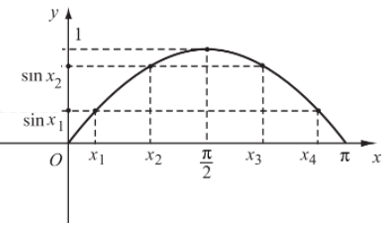
c) Tập giá trị của hàm số y = sinx

Tập giá trị của hàm số này là [– 1; 1].

2. Hàm số y = cosx.

Từ định nghĩa ta thấy hàm số y = cosx:

+ Xác định với mọi x $\in ℝ$ và – 1 ≤ cosx ≤ 1.

+ Là hàm số chẵn.

+ Là hàm số tuần hoàn với chu kì 2π.

Với mọi x $\in ℝ$ ta có: $\sin (x + \frac{π}{2}) = c os x$ .

Từ đó, bằng cách tịnh tiến đồ thị hàm số y = sinx theo vecto $\vec{u} = (\frac{- π}{2}; 0)$ (sang trái một đoạn có độ dài bằng $\frac{π}{2}$ , song song với trục hoành), ta được đồ thị hàm số y = cos x.

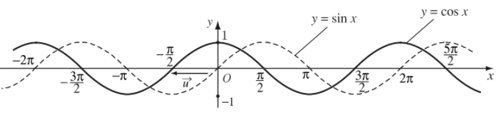
+ Hàm số y = cos x đồng biến trên đoạn [– π; 0] và nghịch biến trên đoạn [0; π].

+ Bảng biến thiên:

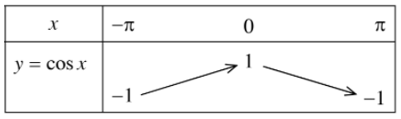
+ Tập giá trị của hàm số y = cosx là [– 1; 1].

+ Đồ thị của các hàm số y = cosx; y = sinx được gọi chung là các đường hình sin.

3. Hàm số y = tanx.

Từ định nghĩa hàm số y = tan x:

+ Có tập xác định: $D = ℝ \ \{\frac{π}{2} + k π; k \in ℤ\}$ .

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì π.

Sự biến thiên và đồ thị hàm số y = tanx trên nửa khoảng $[0; \frac{π}{2})$

+ Hàm số y = tanx đồng biến trên nửa khoảng $[0; \frac{π}{2})$ .

+ Bảng biến thiên:

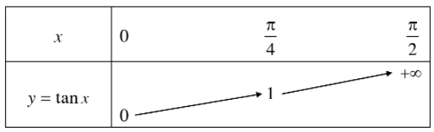
+ Bảng giá trị:

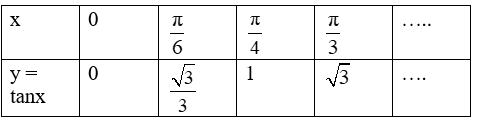
Đồ thị hàm số y = tanx trên nửa khoảng $[0; \frac{π}{2})$ đi qua các điểm tìm được.

4. Hàm số y = cot x

Hàm số y = cotx:

+ Có tập xác định là $D = ℝ \ \{k π; k \in ℤ\}$ .

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì π.

Sự biến thiên của hàm số y = cotx trên khoảng (0; π).

Hàm số y = cotx nghịch biến trên khoàn (0; π).

Bảng biến thiên:

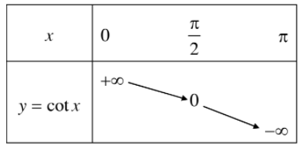
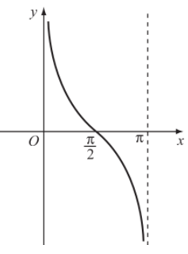
Hình biểu diễn của hàm số y = cotx trên khoảng (0; π).

Xem thêm các bài viết liên quan hay, chi tiết:

Chuyên đề Phương trình lượng giác cơ bản - Toán 11

TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án) – Toán 11

Trắc nghiệm Một số phương trình lượng giác thường gặp (có đáp án)

Câu 9:

Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình $\cos (2 x - \frac{π}{3}) - m = 2$ có nghiệm. Tính tổng T của các phần tử trong S.

A. T = 6

B. T = 3

C. T = -2

D. T = -6

Xem đáp án

Câu 10:

Tìm giá trị thực của tham số m để phương trình $(m - 2) . \sin 2 x = m + 1$ nhận $x = \frac{π}{12}$ làm nghiệm

A. $m \neq 2$

B. $m = \frac{2 (\sqrt{3} + 1)}{\sqrt{3} - 2}$

C. m = -4

D. m = -1

Xem đáp án

Câu 11:

Tìm tất cả các giá trị của tham số m để phương trình $(m - 2) \sin 2 x = m + 1$ vô nghiệm.

A. $m \in [\frac{1}{2}; 2]$

B. $m \in (- \infty; \frac{1}{2}) \cup (2; + \infty)$

C. $m \in (\frac{1}{2}; 2) \cup (2; + \infty)$

D. $m \in (\frac{1}{2}; + \infty)$

Xem đáp án

Câu 12:

Tìm nghiệm dương nhỏ nhất $x_{0}$ của $3 \sin 3 x - \sqrt{3} \cos 9 x = 1 + 4 \sin^{3} 3 x$

A. $x_{0} = \frac{π}{2}$

B. $x_{0} = \frac{π}{18}$

C. $x_{0} = \frac{π}{24}$

D. $x_{0} = \frac{π}{54}$

Xem đáp án

Câu 13:

19/07/2024

Số nghiệm của phương trình $\sin 5 x + \sqrt{3} \cos 5 x = 2 \sin 7 x$ trên khoảng $(0; \frac{π}{2})$ là?

A. 2

B. 1

C. 3

D. 4

Xem đáp án

Câu 14:

Tìm tất cả các giá trị thực của tham số m để phương trình $\cos x + \sin x = \sqrt{2} (m^{2} + 1)$ vô nghiệm.

A. $m \in (- \infty; 1) \cup (1; + \infty)$

B. $m \in (- \infty; 0)$

C. $m \in (0; + \infty)$

D. $m \in (- \infty; 0) \cup (0; + \infty)$

Xem đáp án

Câu 15:

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình $(m + 1) \sin^{2} x - \sin 2 x + \cos 2 x = 0$ có nghiệm

A. 4037

B. 4036

C. 2019

D. 2020

Xem đáp án

Câu 16:

Tính tổng T tất cả các nghiệm của phương trình $2 \sin^{2} \frac{x}{4} - 3 \cos \frac{x}{4} = 0$ trên đoạn $[0; 8 π]$

A. T = 0

B. $T = 8 π$

C. $T = 16 π$

D. $T = 4 π$

Xem đáp án

Câu 17:

Tìm tất cả các giá trị thực của tham số m để phương trình $\tan x + m c o t x = 8$ có nghiệm.

A. $[\begin{matrix} m \leq 16 \\ m \neq 0 \end{matrix}$

B. m < 16

C. $m \geq 16$

D. $m \leq 16$

Xem đáp án

Câu 18:

Tìm tất cả các giá trị thực của tham số m để phương trình $2 c o s^{2} 3 x + (3 - 2 m) \cos 3 x + m - 2 = 0$ có đúng 3 nghiệm thuộc khoảng $(- \frac{π}{6}; \frac{π}{3})$

A. $[\begin{matrix} 1 \leq m \leq 2 \\ m = 3 \end{matrix}$

B. $[\begin{matrix} 1 < m \leq 2 \\ m = 3 \end{matrix}$

C. $1 \leq m \leq 2$

D. $1 \leq m < 2$

Xem đáp án

Câu 19:

23/07/2024

Giải phương trình $s i n^{2} x - (\sqrt{3} + 1) s i n x . c o s x + \sqrt{3} \cos^{2} x = 0$

A. $x = \frac{π}{3} + k 2 π (k \in Z)$

B. $x = \frac{π}{4} + k π (k \in Z)$

C. $[\begin{matrix} x = \frac{π}{3} + k 2 π \\ x = \frac{π}{4} + k 2 π \end{matrix} (k \in Z)$

D. $[\begin{matrix} x = \frac{π}{3} + k π \\ x = \frac{π}{4} + k π \end{matrix} (k \in Z)$

Xem đáp án

Câu 20:

20/07/2024

Số vị trí biểu diễn các nghiệm phương trình $s i n^{2} x - 4 s i n x . c o s x + 4 c o s^{2} x = 5$ trên đường tròn lượng giác là?

A. 4

B. 3

C. 2

D. 1

Xem đáp án

Câu 21:

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;10] để phương trình $11 \sin^{2} x + (m - 2) \sin 2 x + 3 \cos^{2} x = 2$ có nghiệm?

A. 16

B. 21

C. 15

D. 6

Xem đáp án

Câu 22:

21/07/2024

Tìm tất cả các giá trị của tham số m để phương trình $2 s i n^{2} x + m s i n 2 x = 2 m$ vô nghiệm.

A. $0 \leq m \leq \frac{4}{3}$

B. $m < 0; m > \frac{4}{3}$

C. $0 < m < \frac{4}{3}$

D. $m > 0; m < - \frac{4}{3}$

Xem đáp án

Câu 23:

20/07/2024

Giải phương trình $\sin x . \cos x + 2 (\sin x + \cos x) = 2 .$

A. $[\begin{matrix} x = \frac{π}{2} + k π \\ x = k π \end{matrix} (k \in Z)$

B. $[\begin{matrix} x = \frac{π}{2} + k 2 π \\ x = k 2 π \end{matrix} (k \in Z)$

C. $[\begin{matrix} x = - \frac{π}{2} + k π \\ x = k 2 π \end{matrix} (k \in Z)$

D. $[\begin{matrix} x = - \frac{π}{2} + k 2 π \\ x = k π \end{matrix} (k \in Z)$

Xem đáp án

Câu 24:

Từ phương trình $(1 + \sqrt{3}) (\cos + \sin x) - 2 \sin x \cos x - \sqrt{3} - 1 = 0$ , nếu ta đặt $t = \sin x + \cos x$ thì giá trị của t nhận được là:

A. t = 1 hoặc $t = \sqrt{2}$

B. t = 1 hoặc $t = \sqrt{3}$

C. t = 1

D. $t = \sqrt{3}$

Xem đáp án

Câu 25:

23/07/2024

Cho x thỏa mãn $2 \sin 2 x - 3 \sqrt{6} | \sin x + \cos x | + 8 = 0$ . Tính sin2x.

A. $\sin 2 x = - \frac{1}{2}$

B. $\sin 2 x = - \frac{\sqrt{2}}{2}$

C. $\sin 2 x = \frac{1}{2}$

D. $\sin 2 x = \frac{\sqrt{2}}{2}$

Xem đáp án

Câu 26:

20/07/2024

Có bao nhiêu giá trị nguyên của tham số m để phương trình $\sin x . \cos x - \sin x - \cos x + m = 0$ có nghiệm?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Câu 27: