50 câu hỏi trắc nghiệm thuộc Tổng hợp 25 đề thi thử thpt quốc gia môn Toán cực hay, chọn lọc có lời giải (Đề 13)

Câu 1:

21/07/2024

Tính thể tích của một khối lăng trụ biết khối lăng trụ đó có đường cao bằng 3a, diện tích mặt đáy bằng $4 a^{2}$

A. $12 a^{2}$

B. $4 a^{3}$

C. $12 a^{3}$

D. $4 a^{2}$

Xem đáp án

Đáp án C

$V = 3 a . 4 a^{2} = 12 a^{3}$

Do vậy chọn đáp án C

Câu 2:

21/07/2024

Tìm tất cả giá trị thực của tham số m để phương trình có $x^{3} + 3 x^{2} + m = 0$ nghiệm thực phân biệt.

A. $(0; + \infty)$

B. $(0, 4)$

C. $(- \infty; 4) \cup (0; + \infty)$

D. $(- 4; 0)$

Xem đáp án

Câu 3:

21/07/2024

Cho hàm số $y = f (x)$ có tập xác định là $D = (0; + \infty), D = (0; + \infty)$ và $lim_{x \to 0^{+}} y = - \infty; lim_{x \to + \infty} y = + \infty$ . Mệnh đề nào sau đây đúng ?

A. Đồ thị hàm số $y = f (x)$ không có tiệm cận đứng và có tiệm cận ngang.

B. Đồ thị hàm số $y = f (x)$ có tiệm cận đứng và có tiệm cận ngang

C. Đồ thị hàm số $y = f (x)$ có tiệm cận đứng, không có tiệm cận ngang.

D. Đồ thị hàm số $y = f (x)$ không có tiệm cận đứng và không có tiệm cận ngang

Xem đáp án

Đáp án C

Sử dụng định nghĩa về tiệm cận ta thấy các đáp án A, B, D là sai!

Câu 4:

23/07/2024

Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a vuông góc với đáy và $S A = a \sqrt{3}$ Tính thể tích khối chóp S.ABCD

A. $2 a^{3} \sqrt{3}$

B. $4 a^{3} \sqrt{3}$

C. $\frac{4 a^{3} \sqrt{3}}{3}$

D. $\frac{2 a^{3} \sqrt{3}}{3}$

Xem đáp án

Câu 5:

21/07/2024

Kết luận nào sau đây về tính đơn điệu của hàm số $y = \frac{2 x + 1}{x + 1}$ là đúng ?

A. Hàm số nghịch biến trên i

B. Hàm số đồng biến trên mỗi khoảng $(- \infty; - 1) v à (- 1; + \infty)$

C. Hàm số luôn đồng biến trên i

D. Hàm số luôn nghịch biến trên i\{-1}

Xem đáp án

Câu 6:

23/07/2024

Cho hình chóp tứ giác S.ABCD có M, N,P,Q lần lượt là trung điểm các cạnh SA, SB,SC,SD Biết khối chóp S.ABCD có thể tích bằng $16 a^{3}$ Tính thể tích khối chóp S.MNPQ theo a

A. $2 a^{3}$

B. $a^{3}$

C.8 $a^{3}$

D.4 $a^{3}$

Xem đáp án

Câu 7:

21/07/2024

Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng 2a và diện tích của một mặt bên là $a^{2} \sqrt{2}$

A. $\frac{4 a^{3} \sqrt{2}}{3}$

B. $\frac{4 a^{3}}{3}$

C.4 $a^{3}$

D. $\frac{4 a^{3} \sqrt{3}}{3}$

Xem đáp án

Câu 8:

21/07/2024

Cho hình trụ có bán kính đáy bằng 3 cm, độ dài đường cao bằng 4cm Tính diện tích xung quanh của hình trụ này.

A. $24 π (c m^{2})$

B. $22 π (c m^{2})$

C. $26 π (c m^{2})$

D. $20 π (c m^{2})$

Xem đáp án

Đáp án A

Ta có $p = 2 πr = 2 π$ cm

Diện tích của mặt bên là diện tích của hình chữ nhật có chiều dài bằng chu vi hình tròn đáy và chiều rộng bằng chiều cao hình trụ.

$S = 6.4 π = 24 π$ Chọn phương án A.

Câu 9:

21/07/2024

Một ngân hàng đề thi có 50 câu hỏi khác nhau, trong đó có 40% câu hỏi ở mức độ nhận biết, 20% câu hỏi ở mức độ thông hiểu, 30% câu hỏi ở mức độ vận dụng và 10% câu hỏi ở mức độ vận dụng cao. Xây dựng 1 đề thi trắc nghiệm gồm 50 câu hỏi khác nhau từ ngân hàng đề thi đó bằng cách xếp ngẫu nhiên các câu hỏi. Tính xác suất để xây dựng được 1 đề thi mà các câu hỏi được xếp theo mức độ khó tăng dần: nhận biết-thông hiểu-vận dụng-vận dụng cao. (chọn giá trị gần đúng nhất)

A. $4, 56 . 10^{- 26}$

B. $5, 56 . 10^{- 29}$

C. $5, 56 . 10^{- 26}$

D. $4, 56 . 10^{- 29}$

Xem đáp án

Đáp án A

Số cách sắp xếp 50 câu cho một đề thi là 50!

Số cách chọn 20 câu nhận biết để xếp chúng vào đầu tiên là: 20!

Số cách chọn 10 câu thông hiểu để xếp chúng vào vị trí thứ hai là 10!

Số cách chọn 15 câu vận dụng để xếp chúng vào vị trí thứ ba là 15!

Số cách chọn 5 câu vận dụng cao xếp chúng vào vị trí cuối cùng là 5!

Xác suất cần tìm được tính bằng: $P = \frac{20! 10! 15! 5!}{50!} = 4, 56 . 10^{- 26}$

Chọn phương án A

Câu 10:

23/07/2024

Cho x,y là hai số thực dương và m,n là 2 số thực tùy ý. Đẳng thức nào sau đây là sai?

A. $x^{m} . x^{n} = x^{m + n}$

B. ${(x^{m})}^{n} = x^{m . n}$

C. ${(x . y)}^{n} = x^{n} . y^{n}$

D. ${(x^{m})}^{n} = x^{m^{n}}$

Xem đáp án

Đáp án D

Các đáp án A, B, C đều đúng, chỉ có D là sai.

Chọn phương án D.

Câu 11:

23/07/2024

Xác định khoảng nghịch biến của hàm số $y = x^{4} + 2 x^{2} - 3$

A. $(- 3; + \infty)$

B. $(0; + \infty)$

C. $(0; 3)$

D. $(- \infty; 0)$

Xem đáp án

Câu 12:

21/07/2024

Tìm tổng giá trị cực đại và giá trị cực tiểu của hàm số $y = - 2 x^{3} + 3 x^{2} + 18$

A.38

B.37

C.40

D.39

Xem đáp án

Câu 13:

21/07/2024

Một nhà sản xuất độc quyền một loại bánh gia truyền đặc biệt để bán ra thị trường dịp Tết năm nay. Qua thăm dò và nghiên cứu thị trường biết lượng cầu về loại hàng này là một hàm số $Q_{D} (P) = 656 - \frac{1}{2} P$ theo đơn giá bán P Nếu sản xuất loại bánh này ở mức sản lượng Q thì tổng chi phí là C(Q)= $Q^{3} - 77 Q^{2}$ +1000Q + 100 Tìm mức sản lượng Q để doanh nghiệp có lợi nhuận cao nhất sau khi bán hết loại bánh này với đơn giá P, biết lợi nhuận bằng doanh thu trừ đi tổng chi phí, doanh thu bằng đơn giá nhân sản lượng bán được.

A.62

B.200

C.52

D.2

Xem đáp án

Đáp án C

Từ giả thiết ta có P = 1312 – 2Q

Số tiền lãi được tính theo công thức:

$\sum_{} M o n e y = Q . P - f (Q) = (1312 - 2 Q) Q - Q^{3} + 77 Q^{2} - 1000 Q - 100 = - Q^{3} + 75 Q^{2} + 312 Q - 100$

Hàm này đạt GTLN tại . Q=52 Chọn phương án C.

Câu 14:

22/07/2024

Với giá trị nào của tham số m thì đồ thị hàm số $y = x^{4} - 2 (m - 1) x^{2} + m^{4} - 3 m^{2} + 2017$ có 3 điểm cực trị tạo thành một tam giác có diện tích bằng 32

A.m=4

B.m=5

C.m=3

D.m=2

Xem đáp án

Câu 15:

21/07/2024

Tìm giá trị nhỏ nhất của hàm số $y = - 2 x^{4} + 4 x^{2} + 5$ trên đoạn [-2;1]

A.-11

B.-16

C.7

D.5

Xem đáp án

Đáp án D

Tính đạo hàm của hàm số đã cho rồi cho nó bằng 0, ta suy ra được ba điểm cực trị là: (1, 5), (1, 7), và (-1, 7).

GTNN là 5

Chọn phương án D.

Câu 16:

21/07/2024

Tìm tất cả các giá trị của tham số thực m để hàm số $y = \frac{1}{3} x^{3} - m x^{2} + (m^{2} - m + 1) x + 1$ đạt cực đại tại điểm x=1

A.m=2

B.m=3

C.m= -1

D. m=0

Xem đáp án

+ Với m=0 khi đó phương trình y’ = 0 sẽ có nghiệm kép nên loại.

+ Với m=2 thì khi đó phương trình y’=0 có hai nghiệm.

Chọn phương án A.

Câu 17:

21/07/2024

Cho hình chóp SABCD có đáy là hình vuông cạnh bằng a, hai mặt phẳng (SAB), ( SAD) cùng vuông góc với đáy, SC tạo với đáy góc $60 °$ . Tính thể tích khối chóp S.ABCD theo a

A. $\frac{a^{3} \sqrt{2}}{3}$

B. $\frac{a^{3} \sqrt{6}}{3}$

C. $\frac{2 a^{3} \sqrt{6}}{3}$

D. $\frac{4 a^{3} \sqrt{6}}{3}$

Xem đáp án

Câu 18:

21/07/2024

Một học sinh giải bài toán “Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = m x^{3} + m x^{2} + (m - 2) x + 10$ đồng biến trên i” theo các bước như sau:

Bước 1: Hàm số xác định trên i, và $y' = 3 m x^{2} + 2 m x + m - 2$

Bước 2: Yêu cầu bài toán tương đương với $y' > 0, \forall x \in ℝ \Leftrightarrow 3 m x^{2} + 2 m x + m - 2 > 0, \forall x \in ℝ$

Bước 3: $\Leftrightarrow \{\begin{cases} a = 3 m > 0 \\ Δ^{'} = 6 m - 2 m^{2} < 0 \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} m < 0 \\ m > 3 \end{array} \\ m > 0 \end{cases}$

Bước 4: $\Leftrightarrow m > 3.$ Vậy m>3

Hỏi học sinh này đã bắt đầu sai ở bước nào?

A. Bước 2

B. Bước 3

C. Bước 1

D. Bước 4

Xem đáp án

Đáp án B

Để ý thấy lời giải bài toán sai ở bước 3 do m có thể nhỏ hơn 0

Câu 19:

21/07/2024

Cho tứ diện SABCD có ABC là tam giác vuông cân tại A, đường cao SA Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng $60 °$ .Tính theo a thể tích khối tứ diện SABC

A. $\frac{a^{3} \sqrt{6}}{3}$

B. $\frac{a^{3} \sqrt{3}}{3}$

C. $\frac{2 a^{3} \sqrt{6}}{3}$

D. $\frac{a^{3} \sqrt{2}}{3}$

Xem đáp án

Câu 20:

23/07/2024

Cho hình lập phương ABCDA'B'C'D' có cạnh bằng a. Điểm M thuộc đoạn thẳngBC', điểm N thuộc đoạn thẳng AB',MN tạo với mặt phẳng đáy một góc $30 °$ . Tìm độ dài nhỏ nhất của đoạn thẳng MN.

A. $\frac{a}{2}$

B. $\frac{2 a}{3}$

C. $\frac{2 a}{\sqrt{5} - 1}$

D. $\frac{2 a}{\sqrt{5} + 1}$

Xem đáp án

Đáp án D

Ý tưởng: 1 - MN phải chăng sẽ là hai điểm đặc biệt nào đó

2 – Khi nhận ra M là trung điểm của BA’ thì ta tiến hành tính toán MN qua điểm A’ bằng cách lấy P thuộc BC’!

Dễ có mặt phẳng (BA’C’) vuông góc với AB’. Do đó để MN là nhỏ nhất thì M là giao của AB’ và BA’, N là điểm thuộc BC’ sao cho góc giữa MN và (A’B’C’D’) là $30 °$ . Gọi P là điểm thuộc BC’sao cho A’P cũng hợp với mặt phẳng đáy một góc $30 °$ , khi đó MN là đường trung bình của tam giác BA’P nên $M N = \frac{1}{2} A' P$ .

Giả sử độ dài đoạn B’H = x, khi đó PH = HC’ = a – x (tam giác PC’H vuông cân tại C’), và $A' H = \sqrt{A' B'^{2} + B^{'} H^{2}} = \sqrt{a^{2} + x^{2}}$ . Theo điều ta đã giả sử ở trên thì góc giữa A’P và (A’B’C’D’) = $30 °$ , do đó

$\tan (\hat{P A' H}) = \frac{P H}{A' H} = \frac{a - x}{\sqrt{a^{2} + x^{2}}} = \frac{\sqrt{3}}{3}$ hay $\sqrt{a^{2} + x^{2}} = \sqrt{3} (a - x)$ (1)

Mặt khác ta lại có

$A' P = \sqrt{A' H^{2} + H P^{2}} = \sqrt{a^{2} + x^{2} + {(a - x)}^{2}} = \sqrt{4 {(a - x)}^{2}} = 2 (a - x)$ (2)

Từ (1) và (2) ta tính được $A' P = \frac{4 a}{\sqrt{5} + 1}$ . Từ đây ta rút ra được $M N = \frac{2 a}{\sqrt{5} + 1}$ .

Chọn phương án D.

Câu 21:

21/07/2024

Trong các hàm số sau, hàm số nào luôn nghịch biến trên i ?

A. $y = s inx - x$

B. $y = - x^{3} + 3 x^{2}$

C. $y = \frac{2 x + 3}{x + 1}$

D. $y = x^{4} - 3 x^{2} - 1$

Xem đáp án

Đáp án A

Kiểm tra đáp án A thấy có y’ < 0 với mọi giá trị của x, do đó hàm số y=sinx – x luôn ngịch biến trên R.

Câu 22:

23/07/2024

Tính thể tích chóp SABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy.

A. $\frac{a^{3} \sqrt{3}}{2}$

B. $a^{3} \sqrt{3}$

C. $\frac{a^{3} \sqrt{3}}{3}$

D. $\frac{a^{3} \sqrt{3}}{6}$

Xem đáp án

Câu 23:

26/11/2024

Tính thể tích của một khối tứ diện đều cạnh bằng a

A. $\frac{a^{3} \sqrt{2}}{24}$

B. $\frac{a^{3} \sqrt{2}}{12}$

C. $\frac{a^{3} \sqrt{3}}{6}$

D. $\frac{a^{3} \sqrt{3}}{12}$

Xem đáp án

Đáp án đúng: B

*Lời giải:

*Phương pháp giải:

Thể tích: V = 1/3. B .h

( B là diện tích tam giác đáy )

*Lý thuyết nắm thêm về khối đa diện

Khối đa diện đều.

- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:

a) Mỗi mặt của nó là một đa giác đều p cạnh.

b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.

Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.

Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.

- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.

Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.

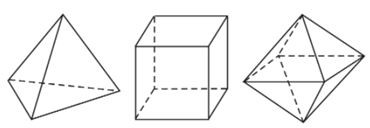
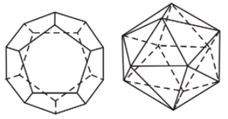
Bảng tóm tắt của năm loại khối đa diện đều.

Thể tích của khối lăng trụ.

Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h

Thể tích khối chóp.

Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là: $V = \frac{1}{3} B . h$ .

Xem thêm các bài viết liên quan hay, chi tiết

Lý thuyết Khối đa diện lồi và khối đa diện đều (mới 2024 + Bài Tập) – Toán 12

50 Bài tập Khối đa diện lồi và khối đa diện đều Toán 12 mới nhất

Câu 24:

21/07/2024

Cho khối chóp SABCD có các điểm A'B'C'D' lần lượt thuộc các cạnh SA,SB,SC thỏa 3SA'=SA,4SB'=SB,5SB'=3SC. Biết thể tích khối chóp SA'B'C' bằng 5 $c m^{3}$ Tìm thể tích khối chóp SABC

A. $120 (c m^{3})$

B. $60 (c m^{3})$

C. $80 (c m^{3})$

D. $100 (c m^{3})$

Xem đáp án

Câu 25:

21/07/2024

Bảng biến thiên sau đây là của hàm số nào?

A. $y = \frac{2 x + 3}{x + 1}$

B. $y = \frac{2 x + 1}{x + 1}$

C. $y = \frac{2 x + 1}{x - 1}$

D. $y = \frac{x + 2}{1 + x}$

Xem đáp án

Đáp án B

Từ BBT ta thấy hàm số không xác định tại x = -1 và hàm số đồng biến trên tập xác định. Do đó ta thấy chỉ có đáp án B là đúng.

Câu 26:

21/07/2024

Cho hình nón tròn xoay có đường cao là $a \sqrt{3}$ , đường kính đáy là 2a Tìm diện tích xung quanh của hình nón đã cho

A. $2 \sqrt{3} π a^{2}$

B. $2 π a^{2}$

C. $π a^{2}$

D. $4 \sqrt{3} . π a^{2}$

Xem đáp án

Đáp án B

Dễ có chu vi của đáy là hình tròn bằng: $p = π d = 2 π a$

Khoảng cách từ đỉnh đến một điểm thuộc vành của hình nón bằng: . $S A = \sqrt{S H^{2} + H A^{2}} = \sqrt{3 a^{2} + a^{2}} = 2 a$

Suy ra diện tích xung quanh hình nón là diện tích hình quạt có bán kính 2a và độ dài cung là $2 π a$ . Ta dễ tính được chu vi của hình tròn bán kinh 2a là $4 π a$ . Do đó diện tích hình quạt cần tính bằng nửa hình tròn này. Từ đây ta thu được kết quả: $S_{x q} = 2 π a^{2}$ .

Chọn đáp án B.

Câu 27:

21/07/2024

Rút gọn biểu thức $K = (\sqrt{x} - \sqrt[4]{x} + 1) (\sqrt{x} + \sqrt[4]{x} + 1) (x - \sqrt{x} + 1) .$

A. $x^{2} + 1$

B. $x^{2} - 1$

C. $x^{2} - x + 1$

D. $x^{2} + x + 1$

Xem đáp án

Đáp án D

Sử dụng liên tiếp hai lần hằng đẳng thức hiệu hai bình phương ta dễ dàng suy ra được đáp án là D.

Câu 28:

21/07/2024

Cho tứ diện đều ABCD có cạnh bằng a Tính khoảng cách từ đỉnh B đến mặt phẳng (ACD)

A. $\frac{a \sqrt{6}}{2}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{a \sqrt{6}}{3}$

D. $\frac{a \sqrt{2}}{3}$

Xem đáp án

Đáp án C

Khoảng cách từ B bằng với chiều cao của tứ diện đều ABCD. Do đó ta dễ dàng suy ra được: $d (B, A C D) = \frac{a \sqrt{6}}{3}$ .

Chọn phương án C.

Câu 29:

21/07/2024

Tính đạo hàm của hàm số $y = \sqrt[3]{x^{2} . \sqrt{x^{3}}}, (x > 0) .$

A. $y' = \frac{4}{3} \sqrt[3]{x}$

B. $y' = \frac{7}{6} . \sqrt[6]{x}$

C. $y' = \frac{6}{7. \sqrt[7]{x}}$

D. $y' = \sqrt[9]{x}$

Xem đáp án

Đáp án B

Ta có $y = \sqrt[6]{x^{7}} = x^{7 / 6} \Rightarrow y' = \frac{7}{6} x^{1 / 6} = \frac{7}{6} \sqrt[6]{x}$ .

Chọn phương án B

Câu 30:

21/07/2024

Cho lăng trụ đứng ABCDA'B'C'D' có đáy là hình bình hành. Các đường chéo DB' và AC' lần lượt tạo với đáy các góc $45 °, 30 °$ Biết chiều cao của lăng trụ là a và BAD = $60 °$ , hãy tính thể tích Vcủa khối lăng trụ này.

A. $V = \frac{a^{3} . \sqrt{2}}{3}$

B. $V = a^{3} . \sqrt{3}$

C. $V = \frac{a^{3}}{2}$

D. $V = \frac{a^{3} . \sqrt{3}}{2}$

Xem đáp án

Câu 31:

23/07/2024

Cho hàm số $y = f (x)$ có $f' (x) > 0, \forall x \in ℝ .$ Tìm tập tất cả các giá trị thực của x để $f (\frac{1}{x}) < f (1) .$

A. $(- \infty; 0) \cup (0; 1)$

B. $(0; 1)$

C. $(1; + \infty)$

D. $(- \infty; 1)$

Xem đáp án

Đáp án C

Theo giả thiết $f' (x) > 0, \forall x \in R$ , do đó $f (\frac{1}{x}) < f (1) \Leftrightarrow \frac{1}{x} < 1 \Leftrightarrow x > 1$

Suy ra với $x \in (1, + \infty)$ thì $f (\frac{1}{x}) < f (1)$ . Chọn phương án C.

Câu 32:

21/07/2024

Cho hàm số $y = a x^{3} + b x^{2} + c x + d, (a, b, c, d \in ℝ)$ có đồ thị như dưới đây. Tìm khẳng định đúng trong các khẳng định sau?

A. $a < 0, b < 0, c < 0, d > 0, b^{2} > 3 a c$

B. $a < 0, b < 0, c > 0, d > 0, b^{2} > 3 a c$

C. $a < 0, b > 0, c < 0, d > 0, b^{2} > 3 a c$

D. $a < 0, b > 0, c > 0, d > 0, b^{2} > 3 a c$

Xem đáp án

Đáp án C

Từ đồ thị hàm số ta suy ra a<0. Để ý rằng đồ thị hàm số giao với Ox tại 3 điểm có hoành độ dương và hai cực trị nằm về hai phía của trục tung. Giải hệ điều kiện đó ta thu được các giá trị a < 0, b > 0, c < 0, và d > 0.

Chọn phương án C.

Câu 33:

21/07/2024

Tính thể tích của một khối lăng trụ tam giác đều ABCDA'B'C'D' có AC' bằng 5a, đáy là tam giác đều cạnh bằng 4a

A. $12 a^{3}$

B. $20 a^{3}$

C. $20 a^{3} \sqrt{3}$

D. $12 a^{3} \sqrt{3}$

Xem đáp án

Đáp án D

Ta có diện tích đáy $S_{d} = 4 \sqrt{3} a^{2}$

Chiều cao: $h = \sqrt{A C'^{2} - A^{'} {C^{'}}^{2}} = 3 a$

Suy ra thể tích hình lăng trụ là: $V = 4 \sqrt{3} a^{2} .3 a = 12 \sqrt{3} a^{3}$

Chọn phương án D.

Câu 34:

21/07/2024

Tìm giá trị lớn nhất của hàm số $y = 1 + \sqrt{4 x - x^{2}}$

A.5

B.3

C.0

D.1

Xem đáp án

Đáp án B

Ta có

$y' = \frac{- 2 x + 4}{2 \sqrt{4 x - x^{2}}} \Rightarrow y' = 0 \Leftrightarrow x = 2 \Rightarrow y (2) = 3$

Chọn phương án B

Câu 35:

21/07/2024

Gọi M;N là giao điểm của đồ thị hàm số và đường thẳng $y = x + 2$ . Khi đó tung độ trung điểm I của đoạn MN bằng bao nhiêu?

A. $- \frac{3}{2}$

B. $\frac{11}{2}$

C. $\frac{7}{2}$

D. $- \frac{7}{2}$

Xem đáp án

Đáp án B

$\frac{7 x + 6}{x - 2} = x + 2 \Leftrightarrow x^{2} - 4 = 7 x + 6 \Leftrightarrow x^{2} - 7 x - 10 = 0 \Rightarrow x = \frac{7 \pm \sqrt{89}}{2} \Rightarrow y = \frac{11 \pm \sqrt{89}}{2}$

Suy ra: $y_{I} = \frac{y_{1} + y_{2}}{2} = \frac{11}{2}$ .

Chọn phương án B.

Câu 36:

21/07/2024

Tìm điểm cực đại của đồ thị hàm số $y = x^{4} - 2 x^{2} + 2$

A. $(- 1; 1)$

B. $(2; 0)$

C. $(1; 1)$

D. $(0; 2)$

Xem đáp án

Đáp án D

Giải phương trình y’(x) = 0 ta thu được ba điểm cực trị là (0, 2), (1, 1), và (-1, 1). Do vậy điểm cực đại là (0, 2).

Chọn phương án D.

Câu 37:

21/07/2024

Bảng biến thiên sau đây là của hàm số nào?

A. $y = x^{3} - 3 x^{2} + 3 x$

B. $y = - x^{3} + 3 x^{2} - 3 x$

C. $y = - x^{3} - 3 x^{2} - 3 x$

D. $y = x^{3} + 3 x^{2} - 3 x$

Xem đáp án

Đáp án A

Từ BBT ta có f’(x)=0 có một nghiệm kép x=1, lại có đây là hàm đồng biến nên đáp án A đúng.

Câu 38:

23/07/2024

Cho hàm số f(x) có $f' (x) = x^{3} {(x - 26)}^{2} (x - 10) .$ Tìm số điểm cực trị của hàm số f(x).

A.4

B.1

C.2

D.3

Xem đáp án

Đáp án C

$f' (x) = x^{3} {(x - 26)}^{2} (x - 10)$ $f' (x) = 0$ có 3 nghiệm nhưng có một nghiệm kép. Do đó có hai điểm cực trị.

Chọn phương án C

Câu 39:

21/07/2024

Cho một tứ diện có đúng một cạnh có độ dài bằng x thay đổi được, các cạnh còn lại có độ dài bằng 2. Tính giá trị lớn nhất của thể tích tứ diện này

A. $\frac{1}{2}$

B. $\frac{2 \sqrt{2}}{3}$

C. $\frac{3 \sqrt{3}}{2}$

D.1

Xem đáp án

Câu 40:

22/07/2024

Cho hàm số $y = \frac{2 x - 3}{4 - x} .$ Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Đồ thị hàm số trên không có điểm cực trị

B. Giao hai tiệm cận là điểm $I (- 2; 4) .$

C. Đồ thị hàm số trên có tiệm cận ngang x=4

D. Đồ thị hàm số trên có tiệm cận đứng y= -2

Xem đáp án

Đáp án A

Dễ có f’(x) < 0 với mọi giá trị của x trong TXĐ. Do đó hàm số đã cho không có cực trị.

Chọn phương án A.

Câu 41:

21/07/2024

Trong các khẳng định sau về hàm số $y = - 2 x^{4} + 4 x^{2} - 1,$ khẳng định nào là SAI ?

A. Đồ thị của hàm số cắt trục Ox tại 2 điểm phân biệt

B. Hàm số có 3 điểm cực trị.

C. Hàm số có 2 điểm cực tiểu và 1 điểm cực đại.

D. Đồ thị của hàm số nhận Oy làm trục đối xứng

Xem đáp án

Đáp án C

Ta có

$y' = - 8 x^{3} + 8 x = - 8 x (x^{2} - 1) \Rightarrow y' = 0 \Leftrightarrow [\begin{matrix} x = 0, y (0) = - 1 \\ x = \pm 1, y (0) = 1 \end{matrix}$

Hàm số có hai điểm cực đại và một điểm cực tiểu.

Chọn phương án C.

Câu 42:

21/07/2024

Cho hình chóp SABCD có đáy là hình thang vuông tại A, B, AD= a, AB=2a, BC=3a,SA=2a . H là trung điểm cạnh AB,SH là đường cao của hình chóp SABCD Tính khoảng cách từ điểm Ađến mp (SCD)

A. $\frac{a \sqrt{30}}{7}$

B. $\frac{a \sqrt{30}}{7}$

C. $\frac{a \sqrt{13}}{10}$

D. $\frac{a \sqrt{13}}{7}$

Xem đáp án

Đáp án B

Gọi $H_{1}$ là chân đường cao kẻ từ H đến DC. $H_{2}$ là chân đường cao kẻ từ H đến $S H_{1}$ . Khi đó ta có

$\begin{array}{l} H H_{1} = a \sqrt{2}, S H = a \sqrt{3} \\ \Rightarrow \frac{1}{H H_{2}} = \sqrt{\frac{1}{H {H_{1}}^{2}} + \frac{1}{S H^{2}}} \\ = \sqrt{\frac{1}{3 a^{2}} + \frac{1}{2 a^{2}}} = \sqrt{\frac{5}{6}} a \\ \Rightarrow H H_{2} = \sqrt{\frac{6}{5}} a \end{array}$

$\Rightarrow d (A, (S C D)) = \frac{\sqrt{30}}{10} a$

Chọn phương án B.

Câu 43:

21/07/2024

Cho hàm số $y = f (x)$ có đồ thị như hình vẽ . Tìm tất cả các giá trị thực của tham số m để phương trình $f (x) - m = 0$ có đúng 2 nghiệm và giá trị tuyệt đối của 2 nghiệm này đều lớn hơn 1

A. $m > - 4$

B. $- 4 < m < - 3$

C. $m > - 3$

D. $- 4 < m \leq - 3$

Xem đáp án

Đáp án C

Khi m > -3 thì phương trình f(x) = m có hai nghiệm lớn hơn 1. Do đó chọn phương án C.

Câu 44:

21/07/2024

Cho hàm sô $y = f (x) = - x^{3} - 3 x^{2} + m .$ Tìm m biết giá trị nhỏ nhất của f(x) trên [-1;1] bằng 0

A.m=2

B.m=4

C.m=0

D.m=6

Xem đáp án

Đáp án C

$\begin{array}{l} f (x) = - x^{3} - 3 x^{2} + m \Rightarrow f' (x) = - 3 x^{2} - 6 x \\ f' (x) = 0 \Leftrightarrow [\begin{matrix} x = 0 \\ x = - 2 (l o a i) \end{matrix} \end{array}$

Tại x=0, ta có $y (0) = m \Rightarrow y (0) = 0 \Leftrightarrow m = 0$

Chọn phương án C.

Câu 45:

21/07/2024

Cho đường cong $y = x^{3} + 3 x^{2} + 3 x + 1$ có đồ thị (C) Phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung là

A. $y = 8 x + 1$

B. $y = 3 x - 1$

C. $y = 3 x + 1$

D. $y = - 8 x + 1$

Xem đáp án

Đáp án C

Ta có (C) giao với trục Oy tại điểm A(0, 1)

$y' = 3 x^{2} + 6 x + 3 \Rightarrow y' (0) = 3$

Suy ra, phương trình tiếp tuyến tại A(0, 1) là:

. $y - y_{0} = y' (x_{0}) (x - x_{0}) \Leftrightarrow y - 1 = 3 x \Leftrightarrow y = 3 x + 1$

Chọn phương án C.

Câu 46:

22/07/2024

Tính chiều dài nhỏ nhất của cái thang để nó có thể dựa vào tường và mặt đất, bắc ngang qua cột đỡ cao 4m Biết cột đỡ song song và cách tường 0,5m, mặt phẳng chứa tường vuông góc với mặt đất- như hình vẽ, bỏ qua đội dày của cột đỡ.

A. $\frac{5 \sqrt{3}}{2}$

B. $\frac{5 \sqrt{5}}{2}$

C. $\frac{3 \sqrt{3}}{2}$

D. $\frac{3 \sqrt{5}}{2}$

Xem đáp án

Câu 47:

21/07/2024

Tính thể tích của khối lập phương có diện tích một mặt chéo bằng $a^{2} \sqrt{2}$ .

A. $2 \sqrt{2} a$

B. $a^{3}$

C. $\sqrt{2} a^{3}$

D. $4 \sqrt{2} a^{3}$

Xem đáp án

Đáp án B

Diện tích mặt chéo là: $a^{2} \sqrt{2}$ . Từ đây ta dễ dàng suy ra độ dài một cạnh của hình lập phương sẽ là a. Do đó thể tích của hình lập phương là $a^{3}$ . Chọn phương án B.

Câu 48:

21/07/2024

Trong một cuộc thi có 10 câu hỏi trắc nghiệm, mỗi câu có 4 phương án trả lời, trong đó chỉ có một phương án đúng. Với mỗi câu, nếu chọn phương án trả lời đúng thì thí sinh sẽ được cộng 5 điểm, nếu chọn phương án trả lời sai sẽ bị trừ 1 điểm. Tính xác suất để một thí sinh làm bài bằng cách lựa chọn ngẫu nhiên phương án được 26 điểm, biết thí sinh phải làm hết các câu hỏi và mỗi câu hỏi chỉ chọn duy nhất một phương án trả lời . (chọn giá trị gần đúng nhất)

A.0.016222

B.0.162227

C.0.028222

D.0.282227

Xem đáp án

Đáp án A

Thí sinh thi được 26 điểm do đó có 6 phương án đúng và 4 phương án sai

Xác suất cần tìm sẽ là:

$P = C_{10}^{6} {(\frac{1}{4})}^{6} {(\frac{3}{4})}^{4} = 0.016222$

Chọn phương án A.

Chú ý: Công thức tổng quát cho bài toán n câu hỏi và a đáp án đúng sẽ là $C_{n}^{a} {(\frac{1}{4})}^{a} {(\frac{3}{4})}^{n - a}$

Câu 49:

21/07/2024

Đồ thị sau đây là của hàm số nào ?

A. $y = \frac{x + 2}{x - 1}$

B. $y = \frac{2 x + 1}{x - 1}$

C. $y = \frac{x + 1}{x - 1}$

D. $y = \frac{x + 2}{1 - x}$

Xem đáp án

Đáp án A

TCĐ: x = 1

TCN: y = 1

Đồ thị hàm số giao với Ox tại x = -2.

Chọn phương án A.

Câu 50:

23/07/2024

Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d (a, b, c, d \in ℝ)$ có bảng biến thiên như hình sau:

Tìm tất cả giá trị thực của tham số m để phương trình $m = |f (x)|$ có 4 nghiệm phân biệt trong đó có đúng một nghiệm dương.

A.m > 2

B.0 < m < 4

C.m > 0

D.2 < m < 4

Xem đáp án

Đáp án D

Hàm số f(x) có dạng $f (x) = (x + 2) {(x - 1)}^{2}$ Giao với trục Oy tại (0, 2) .

=> 2<m<4.

Chọn phương án D.

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3