75 câu trắc nghiệm Giới hạn nâng cao (P1) (Đề số 1)
-
843 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho các số thực a,b thỏa |a| < 1; |b| < 1. Tìm giới hạn I=lim1+a+a2+.........+an1+b+b2+.........+bn.
Xem đáp án
Chọn C.
Ta có 1, a, a2, …, an là một cấp số nhân công bội a nên 
Tương tự 
Suy ra 
( Vì |a| < 1; |b| < 1). ⇒ liman+1 = limbn+1 = 0.
Câu 6:
18/07/2024Giá trị của K=lim(3√n3+n2-1-3√4n2+n+1+5n) bằng:
Xem đáp án
Chọn C.
Ta có:
Do đó: 
.
Câu 7:
21/07/2024Tính giới hạn của dãy số un=12√1+√2+13√2+2√3+....+1(n+1)√n+n√n+1
Xem đáp án
Chọn D.
Ta có:
Suy ra 
Câu 8:
18/07/2024Tính giới hạn của dãy số un=(n+1)√13+23+....+n33n2+n+2
Xem đáp án
Chọn C.
Bằng phương pháp quy nạp, ta chứng minh được:
: 
Suy ra:
Câu 9:
23/07/2024Tính giới hạn của dãy số un=23-123+1.33-133+1..........n3-1n3+1
Xem đáp án
Chọn C.
Ta có
Suy ra 
Câu 11:
20/07/2024Tính giới hạn của dãy số B=lim3√n6+n+1-4√n4+2n-1(2n+3)2
Xem đáp án
Chọn D.
Chia cả tử và mẫu cho n2 ta có được:
Câu 12:
18/07/2024Tính giới hạn của dãy số D=lim(√n2+n+1-23√n3+n2-1+n)
Xem đáp án
Chọn C.
Ta có:
Mà: 
Vậy 
.
Câu 16:
11/11/2024Tính giới hạn:
Xem đáp án
Đáp án đúng là A.
Lời giải
Đặt
Nên 
*Phương pháp giải:
lim un = 0 ⇔ lim|un| = 0
; 
,(k > 0, k ∈ ℕ*); lim nk = +∞,(k > 0, k ∈ ℕ*)
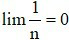
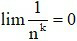
*Lý thuyết
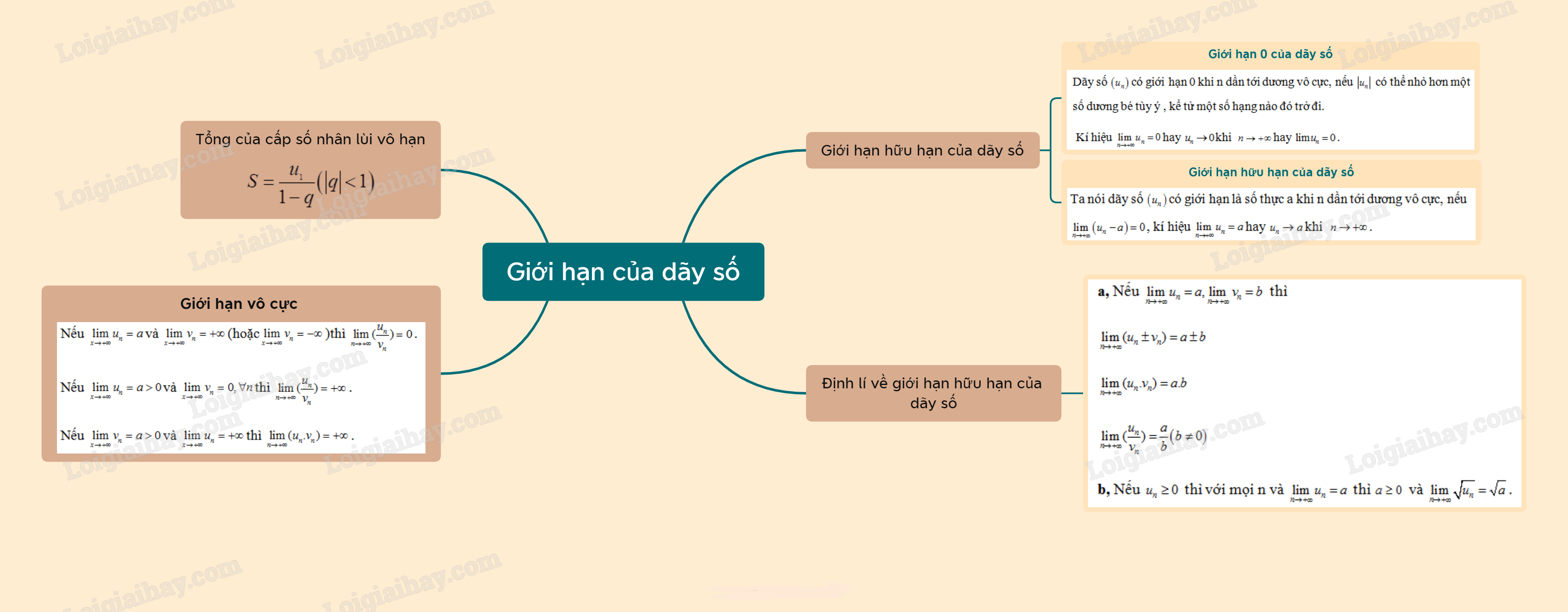
1. Giới hạn hữu hạn của dãy số
Ta nói dãy số có giới hạn 0 khi n dần tới dương vô cực, nếu có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi, kí hiệu hay khi .
Ta nói dãy số có giới hạn là số thực a khi n dần tới dương vô cực, nếu , kí hiệu hay khi .
* Chú ý: Nếu (c là hằng số) thì
2. Định lí về giới hạn hữu hạn của dãy số
a, Nếu thì
b, Nếu thì với mọi n và thì và .
3. Tổng của cấp số nhân lùi vô hạn
4. Giới hạn vô cực của dãy số
Dãy số được gọi là có giới hạn khi nếu có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu hay khi .
Dãy số được gọi là có giới hạn khi nếu , kí hiệu hay khi .
*Quy tắc:
Nếu và (hoặc) thì .
Nếu và thì .
Nếu và thì .
Xem thêm
TOP 40 câu Trắc nghiệm Giới hạn của dãy số (có đáp án ) – Toán 11
.
.Câu 25:
22/07/2024Tìm a để hàm số sau có giới hạn khi
Xem đáp án
Chọn C.
Ta có:
.
Hàm số có giới hạn khi 
Vậy a = 1/2 là giá trị cần tìm.