30 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Ôn tập chương 4

Biết

$\lim u_{n} = 5; \lim v_{n} = a; \lim (u_{n} + 3 v_{n}) = 2018$ , khi đó a bằng

A. 617

B.

$\frac{2018}{3}$

C. $\frac{2023}{3}$

D. 671

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

Ta có:

$\lim (u_{n} + 3 v_{n}) = 2018$

$\Leftrightarrow 5 + 3 a = 2018 \Leftrightarrow a = 671$ .

Câu 2:

18/07/2024

Giá trị của giới hạn

$\lim_{x \to 1} \frac{x - x^{3}}{(2 x - 1) (x^{4} - 3)}$ là

A.

$- \frac{3}{2}$

B. 0

C. – 2

D. 1

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

$\lim_{x \to 1} \frac{x - x^{3}}{(2 x - 1) (x^{4} - 3)}$

$= \frac{1 - 1}{(2.1 - 1) (1 - 3)} = 0$

Câu 3:

Kết quả của giới hạn

$\lim_{x \to - \infty} \frac{2 x^{2} + 5 x - 3}{x^{2} + 6 x + 3}$ là

A. 2

B. 3

C. – 2

D.

$+ \infty$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Ta có

$\begin{array}{l} \lim_{x \to - \infty} \frac{2 x^{2} + 5 x - 3}{x^{2} + 6 x + 3} \\ = \lim_{x \to - \infty} \frac{x^{2} (2 + \frac{5}{x} - \frac{3}{x^{2}})}{x^{2} (1 + \frac{6}{x} + \frac{3}{x^{2}})} \\ = \lim_{x \to - \infty} \frac{2 + \frac{5}{x} - \frac{3}{x^{2}}}{1 + \frac{6}{x} + \frac{3}{x^{2}}} = 2 \end{array}$

Câu 4:

Cho giới hạn

$\lim_{x \to - \infty} \frac{4 x^{3} - 1}{3 x^{2} + x + 2} = - \frac{a}{b}$ với

$a, b \in ℤ$ và

$\frac{a}{b}$ là phân số tối giản. Chọn kết quả đúng trong các kết quả sau:

A.

$a = 11, b = 4$

B. $a = 11, b = 3$

C. $a = 10, b = 3$

D. $a = 11, b = 5$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Ta có $\lim_{x \to - 2} \frac{4 x^{3} - 1}{3 x^{2} + x + 2} = - \frac{11}{4}$ .

Vậy $a = 11$ và $b = 4$

Câu 5:

Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A.

$\lim \frac{1}{n^{k}} = 0$ với k là số nguyên dương.

B. Nếu

$|q| < 1$ thì

$\lim q^{n} = 0$

C. Nếu

$\lim u_{n} = a$ và

$\lim v_{n} = b$ thì

$\lim \frac{u_{n}}{v_{n}} = \frac{a}{b}$

D. Nếu

$\lim u_{n} = a$ và

$\lim v_{n} = + \infty$ thì

$\lim \frac{u_{n}}{v_{n}} = 0$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Vì phải có điều kiện $b \neq 0$

Câu 6:

Tính giới hạn

$\lim_{x \to {(- 2)}^{-}} \frac{3 + 2 x}{x + 2}$

A. 2

B.

$- \infty$

C. $+ \infty$

D. $\frac{3}{2}$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có $\lim_{x \to {(- 2)}^{-}} (3 + 2 x) = - 1 < 0$ ;

$\lim_{x \to {(- 2)}^{-}} (x + 2) = 0$ và khi $x \to {(- 2)}^{-}$ thì $x + 2 < 0$ nên

$\lim_{x \to {(- 2)}^{-}} \frac{3 + 2 x}{x + 2} = + \infty$

Câu 7:

Chọn khẳng định sai trong các khẳng định sau:

A. Hàm số

$y = 5 x^{3} + x - 2$ liên tục trên

$ℝ$

B. Hàm số

$y = \frac{3 x - 5}{x + 3}$ liên tục trên

$ℝ$

C. Hàm số

$y = \frac{2 x^{2} - x}{x + 1}$ liên tục trên

$(- \infty; - 1)$ và

$(- 1; + \infty)$

D. Hàm số

$y = x^{5} + 3 x^{2} + 5$ liên tục trên

$ℝ$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Xét hàm số $y = \frac{3 x - 5}{x + 3}$ ta có

Tập xác định là $D = ℝ \ \{- 3\}$

Hàm số $y = \frac{3 x - 5}{x + 3}$ liên tục trên khoảng $(- \infty; - 3)$ và $(- 3; + \infty)$

Câu 8:

17/07/2024

Trong các giới hạn dãy số dưới đây, giới hạn có kết quả đúng là

A.

$\lim (- 3 n^{4} + 3) = - \infty$

B. $\lim (- 3 n^{4} + 3) = 0$

C. $\lim (- n^{4} + 2) = + \infty$

D. $\lim (5 n^{4} - 2) = - \infty$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

$\lim (- 3 n^{4} + 3) = \lim n^{4} (- 3 + \frac{3}{n^{4}})$

Do $\lim n^{4} = \infty$ $\lim (- 3 + \frac{3}{n^{4}}) = - 3 < 0$ nên

$\lim (- 3 n^{4} + 3) = \lim n^{4} (- 3 + \frac{3}{n^{4}}) = - \infty$

Câu 9:

$\lim_{x \to 3^{+}} \frac{4 x - 3}{x - 3}$ có kết quả là

A. 9

B. 0

C. $- \infty$

D. $+ \infty$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

Ta có: $\lim_{x \to 3^{+}} \frac{4 x - 3}{x - 1} = + \infty$ do

$\{\begin{cases} \lim_{x \to 3^{+}} (4 x - 3) = 9 > 0 \\ \underset{x \to 3^{+}}{\lim (x - 3) = 0 (x - 3 > 0)} \end{cases}$

Câu 10:

Hàm số nào dưới đây gián đoạn tại

$x = - 2$ ?

A.

$y = 2 x^{2} + x - 5$

B.

$y = \frac{x + 5}{x - 2}$

C. $y = \frac{1}{x + 2}$

D. $y = \frac{x - 2}{2 x}$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Hàm số $y = \frac{1}{x + 2}$ bị gián đoạn tại $x = - 2$ vì $y (- 2)$ không tồn tại.

Câu 11:

04/01/2025

Trong các hàm số sau, hàm số nào liên tục tại

$x = 1$ ?

A.

$y = \sqrt{x + 3}$

B. $y = \frac{x + 5}{x - 1}$

C. $y = \frac{3 x}{x^{2} + x - 2}$

D. $y = \sqrt{x - 4}$

Xem đáp án

Đáp án đúng : A

*Lời giải

Hàm số $y = \frac{3 x}{x^{2} + x - 2}$ bị gián đoạn tại $x = 1$ vì $y (1)$ không tồn tại.

*Phương pháp giải

- Cho hàm số y = f(x) có tập xác định D và điểm $x_{0} \in D$ . Để xét tính liên tục của hàm số trên tại điểm x = x₀:

+ Tính giới hạn của hàm số khi $x \to x_{0}$ và tính f(x₀).

+ Nếu tồn tại $\lim_{x \to x_{0}} f (x)$ thì ta so sánh, nếu $\lim_{x \to x_{0}} f (x) = \lim_{x \to x_{0} +} f (x) = \lim_{x \to x_{0} -} f (x) = f (x_{0})$ thì hàm số liên tục tại x₀.

- Lưu ý:

+ Để hàm số liên tục tại x₀, hàm số cần phải xác định tại điểm x₀.

+ < $\lim_{x \to x_{0}} f (x) = a \Leftrightarrow \lim_{x \to x_{0} +} f (x) = \lim_{x \to x_{0} -} f (x) = a$ .

+ Hàm số 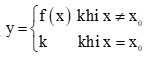liên tục tại x₀ .

+ Hàm số 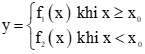liên tục tại x₀ $\Leftrightarrow \lim_{x \to x_{0} +} f_{1} (x) = \lim_{x \to x_{0} -} f_{2} (x) = f_{1} (x_{0})$ .

*Lý thuyết cần nắm thêm về hàm số

HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM

Định nghĩa 1

Cho hàm số y = f(x) xác định trên khoảng K và x₀ ∈ K.

Hàm số y = f(x) được gọi là liên tục tại x₀ nếu $\lim_{x \to x_{0}} f (x) = f (x_{0}) .$

Định nghĩa 2

Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và $\lim_{x \to a^{+}} f (x) = f (a), \lim_{x \to b^{-}} f (x) = f (b) .$

Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.

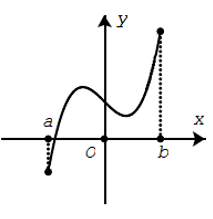
Hàm số liên tục trên khoảng (a;b)

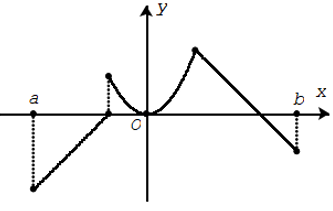
Hàm số không liên tục trên khoảng (a; b).

III. MỘT SỐ ĐỊNH LÍ CƠ BẢN

Định lí 1

a) Hàm số đa thức liên tục trên toàn bộ tập số thực .

b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Định lí 2

Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀;

b) Hàm số $\frac{f (x)}{g (x)}$ liên tục tại x₀ nếu g(x₀) ≠ 0.

Định lí 3

Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0.

Định lí 3 có thể phát biểu theo một dạng khác như sau:

Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).

Xem thêm một số bài viết liên quan hay, chi tiết:

Hàm số liên tục | Lý thuyết, công thức, các dạng bài tập và cách giải

50 bài tập về Hàm số liên tục (có đáp án 2024) và cách giải

Câu 12:

16/07/2024

Tính

$\lim_{x \to + \infty} (- 2 x^{3} - 4 x^{2} + 5)$ .

A. 2

B. 3

C. $- \infty$

D. $+ \infty$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có:

$\begin{array}{l} \lim_{x \to + \infty} (- 2 x^{3} - 4 x^{2} + 5) \\ = \lim_{x \to + \infty} [x^{3} (- 2 - \frac{4}{x} + \frac{5}{x^{3}})] = - \infty \end{array}$ do

$\{\begin{cases} \lim_{x \to + \infty} x^{3} = + \infty \\ \lim_{x \to + \infty} (- 2 - \frac{4}{x} + \frac{5}{x^{3}}) = - 2 < 0 \end{cases}$

Câu 13:

Mệnh đề nào sau đây sai?

A. $\lim \frac{n + 3}{n^{2} + 1} = 0$

B. $\lim \frac{n + 1}{n - 1} = 1$

C. $\lim \frac{1}{2 n + 1} = \frac{1}{2}$

D. $\lim (2 n + 1) = + \infty$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có $\lim \frac{1}{2 n + 1} = \lim \frac{\frac{1}{n}}{2 + \frac{1}{n}} = 0$

Câu 14:

Trong các giới hạn sau đây, giới hạn nào là 0?

Giới hạn

$\lim_{x \to a^{-}} \frac{1}{x - a}$ bằng

A. $+ \infty$

B. 0

C.

$\frac{- 1}{2 a}$

D. $- \infty$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

Ta có:

$\begin{array}{l} \{\begin{cases} \lim_{x \to a^{-}} 1 = 1 > 0 \\ \lim_{x \to a^{-}} (x - a) = 0 \\ x \to a^{-} \Rightarrow x - a < 0 \end{cases} \\ \Rightarrow \lim_{x \to a^{-}} \frac{1}{x - a} = - \infty \end{array}$

Câu 15:

19/07/2024

A.

$\lim 3^{n}$

B.

$\lim \frac{2 n^{2} - 3 n + 1}{n^{3} + 4 n^{2} - 3}$

C.

$\lim n^{k} (k \in ℕ^{*})$

D.

$\lim \frac{n^{3}}{n^{2} + 3}$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Ta có:

$\begin{array}{l} \lim \frac{2 n^{2} - 3 n + 1}{n^{3} + 4 n^{2} - 3} \\ = \lim \frac{\frac{2}{n} - \frac{3}{n^{2}} + \frac{1}{n^{3}}}{1 + \frac{4}{n} - \frac{3}{n^{3}}} = 0 \end{array}$

Câu 16:

Tính giới hạn

$L = \lim_{x \to 1} \frac{|- 2 x|}{x + 1}$ .

A.

$L = - 2$

B. $L = 1$

C. $L = - 1$

D. $L = 2$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

$L = \lim_{x \to 1} \frac{|- 2 x|}{x + 1} = \frac{|- 2|}{2} = 1$

Câu 17:

Giá trị của

$\lim \frac{1}{n^{k}} (k \in ℕ^{*})$ bằng

A. 4

B. 0

C. 2

D. 5

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Ta có: $\lim \frac{1}{n^{k}} = 0$

Câu 18:

$f (x)$ thỏa mãn

$\lim_{x \to 2018^{+}} f (x) = - 2018$ và

$\lim_{x \to 2018^{-}} f (x) = 2018$ . Khi đó khẳng định nào sau đây đúng:

A.

$\lim_{x \to 2018} f (x) = 0$

B. $\lim_{x \to 2018} f (x) = 2018$

C. $\lim_{x \to 2018} f (x) = - 2018$

D. Không tồn tại

$\lim_{x \to 2018} f (x) .$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải :

Chọn D.

Vì $\begin{array}{l} \lim_{x \to 2018} f (x) = L \\ \Leftrightarrow \lim_{x \to 2018^{+}} f (x) = \lim_{x \to 2018^{-}} f (x) = L \end{array}$

Mà đầu bài

$\lim_{x \to 2018^{+}} f (x) = - 2018 \neq 2018 = \lim_{x \to 2018^{-}} f (x)$

Câu 19:

Cho dãy số

$(u_{n}), (v_{n})$ thỏa

$\lim u_{n} = 2, \lim v_{n} = 1$ . Tính

$\lim (2 u_{n} - 3 v_{n})$ .

A. 1

B. 2

C. 3

D. 7

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

$\begin{array}{l} \lim (2 u_{n} - 3 v_{n}) \\ = 2 \lim (u_{n}) - 3 \lim (v_{n}) \\ = 2.2 - 3.1 = 1 \end{array}$

Câu 20:

Trong các giới hạn, giới hạn nào không tồn tại?

Hàm số

$y = f (x)$ có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?

A. 0

B. 1

C. 3

D. 2

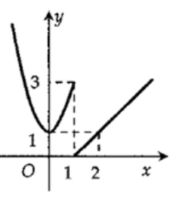
Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Đồ thị hàm số $y = f (x)$ gián đoạn tại điểm có hoành độ $x = 1$

Câu 21:

19/07/2024

Cho $\lim_{x \to 1} \frac{\sqrt{x + 1} - 2}{2 - x} = \sqrt{a} - b$ với $a, b \in ℕ, 0 \leq a, b \leq 3$ , khi đó $a + 2 b$ bằng

A. 3

B. 6

C. 4

D. 2

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

$\lim_{x \to 1} \frac{\sqrt{x + 1} - 2}{2 - x} = \sqrt{2} - 2$

suy ra $a = 2, b = 2$ nên $a + 2 b = 6$

Câu 22:

18/07/2024

A.

$\lim_{x \to 3} (x^{2} - 3 x + 2)$

B. $\lim_{x \to 3} \sqrt{16 - x^{2}}$

C. $\lim_{x \to 3} \frac{x^{2} - 9}{x + 3}$

D. $\lim_{x \to 3} \sqrt{x^{2} - 9}$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

Ta có

$\begin{array}{l} x^{2} - 9 > 0 \\ \Leftrightarrow x \in (- \infty; - 3) \cup (3; + \infty) \end{array}$

$\lim_{x \to 3^{+}} \sqrt{x^{2} - 9} = 0$ và $\lim_{x \to 3^{-}} \sqrt{x^{2} - 9}$ không tồn tại nên không tồn tại $\lim_{x \to 3} \sqrt{x^{2} - 9}$

Câu 23:

Cho a là một hằng số,

$\lim_{x \to + \infty} \frac{a \sqrt{x^{2} - 2 x} + x - 3}{2 + \sqrt{x^{2} + 1}}$ có giá trị bằng

A.

$\frac{a + 1}{2}$

B. a

C.

$a + 1$

D. $1 - a$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có:

$\begin{array}{l} \lim_{x \to + \infty} \frac{a \sqrt{x^{2} - 2 x} + x - 3}{2 + \sqrt{x^{2} + 1}} \\ = \lim_{x \to + \infty} \frac{a \sqrt{1 - \frac{2}{x}} + 1 - \frac{3}{x}}{\frac{2}{x} + \sqrt{1 + \frac{1}{x^{2}}}} \\ = a + 1 \end{array}$

Câu 24:

$f (x) = \{\begin{cases} \frac{\sqrt{x} - 2}{x - 4} k h i x > 4 \\ a x + \frac{5}{4} k h i x \leq 4 \end{cases}$ , trong đó a là một hằng số đã biết. Hàm số có giới hạn hữu hạn tại

$x = 4$ khi và chỉ khi

A. $a = 1$

B. $a = - 1$

C.

$a = - \frac{1}{4}$

D. $a = \frac{1}{4}$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có

$\begin{array}{l} \lim_{x \to 4^{+}} \frac{\sqrt{x} - 2}{x - 4} \\ = \lim_{x \to 4^{+}} \frac{x - 4}{(x - 4) (\sqrt{x} - 2)} \\ = \lim_{x \to 4^{+}} \frac{1}{(\sqrt{x} + 2)} = \frac{1}{4} \end{array}$

$\lim_{x \to 4^{+}} (a x + \frac{5}{4}) = 4 a + \frac{5}{4}$

Hàm số có giới hạn hữu hạn tại $x = 4$ khi và chỉ khi

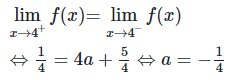
Câu 25:

Tìm giá trị thực của tham số m để hàm số

$f (x) = \{\begin{cases} \frac{x^{2} - x - 2}{x - 2} k h i x \neq 2 \\ m k h i x = 2 \end{cases}$ liên tục tại

$x = 2$

A.

$m = 0$

B. $m = 2$

C.

$m = 1$

D. $m = 3$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

$\begin{array}{l} \lim_{x \to 2} \frac{x^{2} - x - 2}{x - 2} \\ = \lim_{x \to 2} (x + 1) = 3 \end{array}$

$f (2) = m$

Hàm số liên tục tại $x = 2 \Leftrightarrow m = 3$

Câu 26:

Biết rằng

$\lim_{x \to - \sqrt{3}} \frac{5 x^{3} + 15 \sqrt{3}}{3 - x^{2}} = a \sqrt{3} + b$ với

$a, b \in ℚ$ . Tính

$a^{2} + b^{2}$

A.

$\frac{15}{2}$

B. $\frac{225}{4}$

C.

$\frac{- 225}{4}$

D. $\frac{225}{2}$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Ta có:

$\begin{array}{l} \lim_{x \to - \sqrt{3}} \frac{5 x^{3} + 15 \sqrt{3}}{3 - x^{2}} \\ = \lim_{x \to - \sqrt{3}} \frac{5 (x + \sqrt{3}) (x^{2} - x \sqrt{3} + 3)}{(\sqrt{3} - x) (\sqrt{3} + x)} \\ = \lim_{x \to - \sqrt{3}} \frac{5 (x^{2} - x \sqrt{3} + 3)}{\sqrt{3} - x} \\ = \frac{15 \sqrt{3}}{2} \end{array}$

$\Rightarrow a = \frac{15}{2}, b = 0$

Vậy $a^{2} + b^{2} = \frac{225}{4}$ .

Câu 27:

16/07/2024

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{3} - x^{2} + 2 x - 2}{x - 1} k h i x \neq 1 \\ 3 x + m k h i x = 1 \end{cases}$ . Để $f (x)$ liên tục tại $x = 1$ thì m bằng

A. 1

B. 0

C. 2

D. – 1

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Ta có:

$\begin{array}{l} \lim_{x \to 1} f (x) \\ = \lim_{x \to 1} \frac{x^{3} - x^{2} + 2 x - 2}{x - 1} \\ = \lim_{x \to 1} (x^{2} + 2) = 3 \end{array}$

$f (1) = 3 + m$

Hàm số đã cho liên tục tại $x = 1$ khi và chỉ khi

$\lim_{x \to 1} f (x) = f (1)$ $\Leftrightarrow 3 + m = 3 \Leftrightarrow m = 0$

Câu 28:

$f (x) = \{\begin{cases} 3 x + a - 1 k h i x \leq 0 \\ \frac{\sqrt{1 + 2 x} - 1}{x} k h i x > 0 \end{cases}$ . Tìm tất cả giá trị của a để hàm số đã cho liên tục tại điểm

$x = 0$ .

A.

$a = 1$

B. $a = 3$

C.

$a = 2$

D. $a = 4$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có $f (0) = a - 1$ và $\lim_{x \to 0^{+}} f (x) = a - 1,$

$\lim_{x \to 0^{-}} f (x)$

$= \lim_{x \to 0^{-}} \frac{\sqrt{1 + 2 x} - 1}{x}$

$= \lim_{x \to 0^{-}} \frac{2}{\sqrt{1 + 2 x} + 1} = 1$

Hàm số đã cho liên tục tại điểm $x = 0$ khi $x = 0$

$\begin{array}{l} \lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{-}} f (x) \\ \Leftrightarrow a - 1 = 1 \Leftrightarrow a = 2 \end{array}$

Câu 29:

Trong các giới hạn dưới đây, giới hạn nào bằng

$+ \infty$ ?

A.

$\lim_{x \to 4^{-}} \frac{2 x - 1}{4 - x}$

B. $\lim_{x \to + \infty} (- x^{3} + 2 x + 3)$

C. $\lim_{x \to - \infty} \frac{x^{2} + x + 1}{x - 1}$

D. $\lim_{x \to 4^{+}} \frac{2 x - 1}{4 - x}$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Ta có:

$\lim_{x \to 4^{-}} \frac{2 x - 1}{4 - x} = + \infty$

$\lim_{x \to + \infty} [x^{3} (- 1 + \frac{2}{x^{2}} + \frac{3}{x^{3}})] = - \infty$

$\lim_{x \to - \infty} \frac{x^{2} + x + 1}{x - 1}$

$= \lim_{x \to - \infty} \frac{1 + \frac{1}{x} + \frac{1}{x^{2}}}{\frac{1}{x} - \frac{1}{x^{2}}} = - \infty$

$\lim_{x \to 4^{+}} \frac{2 x - 1}{4 - x} = - \infty$

Câu 30: