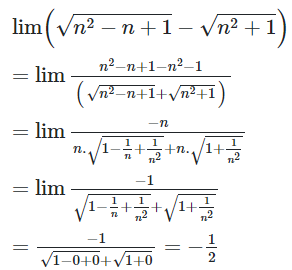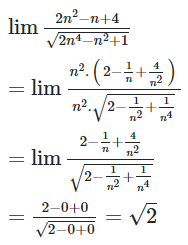Trắc nghiệm Giới hạn của dãy số (có đáp án)
Trắc nghiệm Toán 11 Bài 1: Giới hạn của dãy số
-
585 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho cấp số nhân un=12n, . Khi đó:
 Xem đáp án
Xem đáp án
Cấp số nhân đã cho là cấp số nhân lùi vô hạn có:
Đáp án cần chọn là: A
Câu 2:
22/07/2024Dãy số nào sau đây có giới hạn 0 ?
 Xem đáp án
Xem đáp án
Dãy số mà có giới hạn 0.
Đáp án cần chọn là: B
Câu 3:
22/07/2024Cho là một cấp số nhân công bội và số hạng đầu ,
Đặt . Giá là:
 Xem đáp án
Xem đáp án
Do nên cấp số nhân đã cho là cấp số nhân lùi vô hạn:
Đáp án cần chọn là: D
Câu 4:
18/07/2024Cấp số nhân có . Đặt ), khi đó:
 Xem đáp án
Xem đáp án
Vì nên đây là tổng n số hạng đầu của cấp số nhân công bội
.
Theo công thức tính tổng ta được:
Đáp án cần chọn là: A
Câu 8:
20/07/2024Cho hai dãy số , với ,.
Biết . Chọn kết luận không đúng:
 Xem đáp án
Xem đáp án
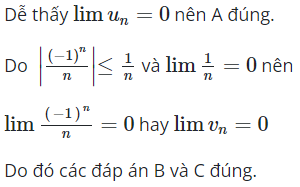
Đáp án cần chọn là: D
Câu 12:
22/07/2024Chọn kết luận không đúng:
 Xem đáp án
Xem đáp án
Ta thấy:
Mà nên các đáp án A, B, D đúng.
Vì nên nên C sai.
Đáp án cần chọn là: C
Câu 13:
22/07/2024Cho dãy số có giới hạn . Chọn kết luận đúng:
 Xem đáp án
Xem đáp án
Vì nên
Đáp án cần chọn là: B
Câu 16:
23/07/2024Cho các dãy số có . Chọn đáp án đúng:
 Xem đáp án
Xem đáp án
Đáp án A:
nên A sai.
Đáp án B:
nên B đúng.
Đáp án C:
nên C sai.
Đáp án D:
nên D sai.
Đáp án cần chọn là: B
Câu 28:
21/07/2024Cho các số thực a, b thỏa .
Tìm giới hạn
 Xem đáp án
Xem đáp án
Ta có là một cấp số nhân có công bội q = a
Tương tự:
Đáp án cần chọn là: C
Câu 29:
22/07/2024Cho dãy số xác định bởi . Khi đó mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chứng minh bằng quy nạp:
* Với
đúng
* Giả sử (*) đúng với , tức là ta chứng minh (*) đúng với ,
tức là cần chứng minh
Ta có :
Theo nguyên lý quy nạp, ta chứng minh được (*).
Như vậy, công thức tổng quát của dãy là:
Từ (*) ta có
⇒ là dãy giảm và
⇒ là dãy giảm tới 1 khi n→+∞
Đáp án cần chọn là: A
Câu 30:
22/07/2024Tính giới hạn của dãy số với
 Xem đáp án
Xem đáp án
Ta có:
Do là cấp số nhân có công bội q nên:
(1)
Mà:
Từ (1); (2) suy ra:
Do nên
Suy ra
Đáp án cần chọn là: C
Có thể bạn quan tâm
- Trắc nghiệm Giới hạn của dãy số (có đáp án) (584 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 1 (Có đáp án ): Giới hạn của dãy số (317 lượt thi)
- Trắc nghiệm Giới hạn của dãy số có đáp án (phần 2) (306 lượt thi)
- Trắc nghiệm Giới hạn của dãy số có đáp án (Nhận biết) (283 lượt thi)
- Trắc nghiệm Giới hạn của dãy số có đáp án (Thông hiểu) (304 lượt thi)
- Trắc nghiệm Giới hạn của dãy số có đáp án (Vận dụng) (341 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Giới hạn của hàm số (có đáp án) (1229 lượt thi)
- Trắc nghiệm Ôn tập chương 4 (có đáp án) (1228 lượt thi)
- 75 câu trắc nghiệm Giới hạn cơ bản (P1) (797 lượt thi)
- 75 câu trắc nghiệm Giới hạn nâng cao (P1) (737 lượt thi)
- Trắc nghiệm Hàm số liên tục (có đáp án) (664 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 3 (Có đáp án): Hàm số liên tục (410 lượt thi)
- Trắc nghiệm Hàm số liên tục có đáp án (Nhận biết) (332 lượt thi)
- Trắc nghiệm Giới hạn của hàm số có đáp án (Nhận biết) (321 lượt thi)
- Trắc nghiệm Hàm số liên tục có đáp án (Vận dụng) (317 lượt thi)
- Trắc nghiệm Giới hạn của hàm số có đáp án (Thông hiểu) (311 lượt thi)