Trắc nghiệm Ôn tập chương 4 (có đáp án)
Trắc nghiệm Toán 11 Ôn tập chương 4
-
1236 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 4:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có .
Vậy và
Câu 5:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Vì phải có điều kiện
Câu 7:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Xét hàm số ta có
Tập xác định là
Hàm số liên tục trên khoảng và
Câu 8:
16/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Do nên
Câu 10:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Hàm số bị gián đoạn tại vì không tồn tại.
Câu 11:
04/01/2025 Xem đáp án
Xem đáp án
Đáp án đúng : A
*Lời giải
Hàm số bị gián đoạn tại vì không tồn tại.
*Phương pháp giải
- Cho hàm số y = f(x) có tập xác định D và điểm . Để xét tính liên tục của hàm số trên tại điểm x = x0:
+ Tính giới hạn của hàm số khi và tính f(x0).
+ Nếu tồn tại thì ta so sánh, nếu thì hàm số liên tục tại x0.
- Lưu ý:
+ Để hàm số liên tục tại x0, hàm số cần phải xác định tại điểm x0.
+ <.
+ Hàm số 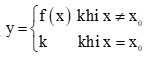
+ Hàm số 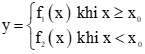
*Lý thuyết cần nắm thêm về hàm số
HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
Định nghĩa 1
Cho hàm số y = f(x) xác định trên khoảng K và x0 ∈ K.
Hàm số y = f(x) được gọi là liên tục tại x0 nếu
Định nghĩa 2
Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.
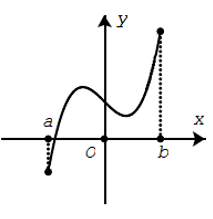
Hàm số liên tục trên khoảng (a;b)
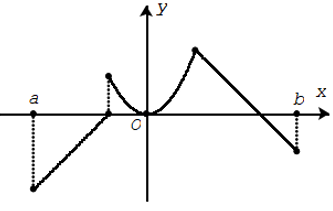
Hàm số không liên tục trên khoảng (a; b).
III. MỘT SỐ ĐỊNH LÍ CƠ BẢN
Định lí 1
a) Hàm số đa thức liên tục trên toàn bộ tập số thực .
b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Định lí 2
Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x0. Khi đó:
a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x0;
b) Hàm số liên tục tại x0 nếu g(x0) ≠ 0.
Định lí 3
Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0.
Định lí 3 có thể phát biểu theo một dạng khác như sau:
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).
Xem thêm một số bài viết liên quan hay, chi tiết:
Hàm số liên tục | Lý thuyết, công thức, các dạng bài tập và cách giải
Câu 15:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có:
Câu 18:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải :
Chọn D.
Vì
Mà đầu bài
Câu 20:
19/07/2024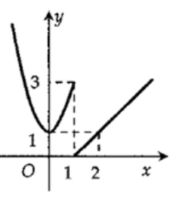
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Đồ thị hàm số gián đoạn tại điểm có hoành độ
Câu 22:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Ta có
và không tồn tại nên không tồn tại
Câu 23:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Ta có:
Câu 24:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Ta có
Hàm số có giới hạn hữu hạn tại khi và chỉ khi
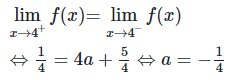
Câu 25:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Hàm số liên tục tại
Câu 27:
16/07/2024Cho hàm số . Để liên tục tại thì m bằng
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có:
Hàm số đã cho liên tục tại khi và chỉ khi
Câu 28:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Ta có và
Hàm số đã cho liên tục tại điểm khi
Câu 29:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có:
Câu 30:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có hàm số nên hàm số liên tục trên mỗi khoảng và
Ta có và
Hàm số liên tục trên thì hàm số liên tục tại hay
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập chương 4 (có đáp án) (1235 lượt thi)
- 75 câu trắc nghiệm Giới hạn cơ bản (P1) (805 lượt thi)
- 75 câu trắc nghiệm Giới hạn nâng cao (P1) (752 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Giới hạn của hàm số (có đáp án) (1241 lượt thi)
- Trắc nghiệm Hàm số liên tục (có đáp án) (672 lượt thi)
- Trắc nghiệm Giới hạn của dãy số (có đáp án) (590 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 3 (Có đáp án): Hàm số liên tục (419 lượt thi)
- Trắc nghiệm Giới hạn của dãy số có đáp án (Vận dụng) (347 lượt thi)
- Trắc nghiệm Hàm số liên tục có đáp án (Nhận biết) (337 lượt thi)
- Trắc nghiệm Giới hạn của hàm số có đáp án (Thông hiểu) (331 lượt thi)
- Trắc nghiệm Giới hạn của hàm số có đáp án (Nhận biết) (328 lượt thi)
- Trắc nghiệm Đại số và Giải tích 11 Bài 1 (Có đáp án ): Giới hạn của dãy số (322 lượt thi)
- Trắc nghiệm Hàm số liên tục có đáp án (Vận dụng) (322 lượt thi)
