70 câu trắc nghiệm Dãy số, Cấp số cộng, Cấp số nhân nâng cao (P1) (Đề số 1)
-
825 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Cho dãy số (un) với . Số hạng tổng quát của dãy số là số hạng nào dưới đây?
Xem đáp án
Chọn C.
Ta có: 
Cộng hai vế ta được un = 1 + 12 + 22 +… + (n -1)2 = 
Câu 2:
22/07/2024Cho dãy số (un) với .Số hạng tổng quát của dãy số là số hạng nào dưới đây?
Xem đáp án
Chọn A.
Ta có: 
Cộng hai vế ta được un = 2 + 1 + 3 + 5 + … + (2n – 3) = 2 + (n – 1)2
Câu 3:
17/07/2024Xét tính tăng, giảm và bị chặn của dãy số (un), biết:
Xem đáp án
Chọn B.
Ta có:
⇒ un+1 > un ∀ n ≥ 1 ⇒ dãy (un) là dãy số tăng.
un > 
= n + 1 ≥ 2 ⇒ dãy (un) bị chặn dưới.
Câu 4:
16/07/2024Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức Sn = 4n – n2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
Xem đáp án
Chọn D.
Ta có: 
Câu 5:
22/07/2024Cho tam giác ABC nhọn biết 3 góc của tam giác lập thành một cấp số cộng ; số đo góc A nhỏ nhất và .Tìm các góc của tam giác?
Xem đáp án
Chọn A.
Ta có 
và tam giác ABC nhọn nên A = 45º.
A + B + C = 180 º ⇒ B + C = 180º - 45º = 135º
Do 3 góc tam giác lập thành cấp số cộng ; số đo góc A nhỏ nhất nên B = A + d; C = A + 2d.
Khi đó: B + C = A + d + A + 2d = 2A + 3d ⇒ 3d = 135º - 2.45º = 45º
⇒ d = 15º ⇒ B = A + d = 60º; C = A + 2d = 75º
Câu 6:
23/07/2024Cho tứ giác ABCD biết 4 góc của tứ giác lập thành một cấp số cộng và tan A không xác định; B ≤ A ≤ C ≤ D . Tìm các góc còn lại?
Xem đáp án
Chọn D.
Ta có: B ≤ A ≤ C ≤ D nên A < 180º
Lại có tan A không xác định nên A = 90º
Do 4 góc tứ giác lập thành cấp số cộng và B ≤ A ≤ C ≤ D nên
B = 90 - d; C = 90 + d; D = 90 + 2d.
Ta có: A + B + C + D = 360 ⇒ 90 + 90 – d + 90 + d + 90 + 2d = 360
⇒ d = 0 ⇒ A = B = C = D = 90º.
Câu 7:
21/07/2024Cho cấp số cộng (un); công sai d. Biết u2 + u22 = 40. Tính S23
Xem đáp án
Chọn C.
Ta có: u2 + u22 = 40 ⇔ u1 + d + u1 + 21d = 40 ⇔ 2u1 + 22d = 40
Mà 
Câu 8:
18/07/2024Cho cấp số cộng (un); công sai d. Biết u1 + u4 + u7 + u10 + u13 + u16 = 147. Tính u1 + u6 + u11 + u16
Xem đáp án
Chọn B.
Ta có : u1 + u4 + u7 + u10 + u13 + u16 = 147
⇔ u1 + u1 + 3d + u1 + 6d + u1 + 9d + u1 + 12d + u1 + 15d = 147
⇔ 6 u1 + 45d = 147 ⇔ 2 u1 + 15d = 49
Ta có: u1 + u6 + u11 + u16 = u1 + u1 + 5d + u1 + 10d + u1 + 15d = 4u1 + 30d
= 2(2u1 + 15d) = 2.49 = 98.
Câu 9:
21/07/2024Cho cấp số cộng (un); công sai d. Biết u4 + u8 + u12 + u16 = 224. Tính: S19
Xem đáp án
Chọn A.
Ta có: u4 + u8 + u12 + u16 = 224 ó u1 + 3d + u1 + 7d + + u1 + 15d = 224
⇔ 4 u1 + 36d = 224 ⇔ u1 + 9d = 56
Ta có: S19 = (19/2).(2 u1 + 18d) = 19(u1 + 9d) = 19.56 = 1064
Câu 10:
22/07/2024Cho cấp số cộng (un); công sai d. Biết u23 + u57 = 29. Tính: u10 + u70 + u157 +3u1
Xem đáp án
Chọn D.
Ta có:
+) u23 + u57 = 29 ⇔ u1 + 22d + u1 + 56d = 29 ⇔ 2 u1 + 78d = 29
+) 3 u1 + u10 + u70 + u157 = 3 u1 + u1 + 9d + u1 + 69d + u1 + 156d = 6 u1 + 234d
= 3(2 u1 + 78d) = 3.29 = 87
Câu 11:
21/07/2024Bốn số nguyên lập thành cấp số cộng, biết tổng của chúng bằng 20, tổng nghịch đảo của chúng bằng 25/24. Tìm công sai d?
Xem đáp án
Chọn D.
Gọi bốn số hạng liên tiếp của cấp số cộng là u1 = u – 3d, u2 = u – d, u3 = u + d, u4 = u + 3d với công sai là 2d:
Theo đề bài ta có:
Giải (2): đặt t = d2, điều kiện t ≥ 0
⇔ 24(100 – 20t) =5 (25 – 9t)(25 – t)24. (20 - 4t) = (25- 9t). ( 25- t)
⇔ 9t2 – 154t + 145 = 0 ⇔ t = 1 ∨ t = 145/9
Vì các số hạng là những số nguyên nên chọn t = 1.
Khi đó d2 =1 ⇒ d = 1; d = -1.
Câu 12:
17/07/2024Cho dãy số (an) xác định bởi .Mệnh đề nào dưới đây là mệnh đề đúng?
Xem đáp án
Chọn C.
Kiểm tra từng phương án đến khi tìm được đáp án đúng.
+ Ta có 
+ Ta có:
+ Ta có 
+ Ta có
Câu 13:
22/07/2024Cho dãy số có tổng của n số hạng đầu tiên bằng Sn = n3. Mệnh đề nào dưới đây là đúng?
Xem đáp án
Chọn A.
Ta có a1 + a2 + … + an = Sn = n3 và có a1 + a2 + … + an-1 = Sn-1 = (n – 1)3.
Suy ra an = Sn – Sn-1 = n3 – (n – 1)3 = 3n2 – 3n + 1.
Ta có an = 3n2 – 3n + 1.
và an-1 = 3(n – 1)2 – 3(n – 1) + 1 = 3n2 – 9n + 7.
Do đó an – an-1 = 6n – 6 ≥ 0.
Dấu bằng chỉ xảy ra khi n – 1 = 0 hay n = 1. suy ra dãy số (an) là dãy số tăng.
Câu 15:
05/12/2024Người ta trồng 3003 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây; hàng thứ 2 có 2 cây; hàng thứ 3 có 3 cây...hỏi có bao nhiêu hàng?
Xem đáp án
Đáp án đúng là B
Lời giải
Gọi số hàng cây là n.
Số cây lần lượt trên các hàng là 1; 2; 3..; n.
Đây là một cấp số cộng với số hạng đầu u1 = 1; d = 1 .
Tổng số cây trên n hàng là:
Vậy số hàng cần tìm là 77.
*Phương pháp giải
Nhận dạng đó là 1 cấp số cộng.
(un) là cấp số cộng khi un+1 = un + d, n ∈ N* (d gọi là công sai)
Số hạng tổng quát của cấp số cộng (un) được xác định bởi công thức:
un = u1 + (n – 1)d với n ∈ N*, n ≥ 2.
Tổng n số hạng đầu tiên Sn được xác định bởi công thức:
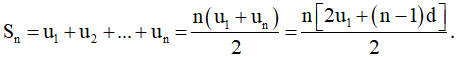
* Lý thuyết
Định nghĩa.
- Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ sai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
- Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi:
un+1 = un + d với (1)
- Đặc biệt, khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).
Số hạng tổng quát
- Định lí: Nếu cấp số cộng (un) có số hạng đầu u1 và công sai d thì số hạng tổng quát un được xác định bởi công thức:
un = u1 + (n – 1)d với n ≥ 2.
Tính chất các số hạng của cấp số cộng.
- Định lí 2:
Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và số cuối) đều là trung bình cộng của hai số đứng kề với nó, nghĩa là:
Tổng n số hạng đầu của một cấp số cộng
- Định lí: Cho cấp số cộng (un). Đặt Sn = u1 + u2 + u3 + … + un.
Khi đó: .
- Chú ý: vì un = u1 + (n – 1)d nên ta có: .
Xem thêm
Câu 16:
22/07/2024Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số cộng: x3 – 3x2 – 9x + m = 0
Xem đáp án
Chọn D.
Cách 1: Giải bài toán như cách giải tự luận.
- Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x1; x2; x3 lập thành một cấp số cộng.
Theo định lý Vi-ét đối với phương trình bậc ba, ta có x1 + x2 + x3 = 3 (1)
Vì x1; x2; x3 lập thành cấp số cộng nên x1 + x3 = 2x2 (2)
Từ (1) và (2) suy ra 3x2 = 3 ⇔ x2 = 1.
Thay x2 = 1 vào phương trình đã cho, ta được
1 - 3.1 - 9.1 + m = 0 suy ra m = 11
- Điều kiện đủ:
+ Với m = 11 thì ta có phương trình x3 – 3x2 – 9x + 11 = 0 ⇔ 
Ba nghiệm này lập thành một cấp số cộng nên m = 11 là giá trị cần tìm.
Câu 17:
22/07/2024Biết rằng tồn tại giá trị của tham số m để phương trình sau có bốn nghiệm phân biệt lập thành một cấp số cộng: x4 – 2(m + 1)x2 + 2m + 1 = 0, tính lập phương của giá trị đó.
Xem đáp án
Chọn C.
Đặt t = x2.
Khi đó ta có phương trình: t2 – 2(m + 1)t + 2m + 1 = 0 (*)
Phương trình đã cho có nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
+ Với điều kiện trên thì phương trình (*) có hai nghiệm dương phân biệt là t1 < t2.
Khi đó phương trình đã cho có bốn nghiệm phân biệt là 
.
Bốn nghiệm này lập thành một cấp số cộng khi
Theo định lý Vi-ét ta có: t1 + t2 = 2(m + 1) ; t1.t2 = 2m + 1.
Suy ra ta có hệ phương trình 
Chỉ có m = 4 thỏa mãn điều kiện .
Do đó 43 = 64.
Câu 18:
21/07/2024Cho 2 cấp số cộng : 5 ;8 ;11 ; .....và 3 ;7 ;11,....Hỏi trong 100 số hạng đầu tiên của mỗi cấp số ; có bao nhiêu số hạng chung ?
Xem đáp án
Chọn C.
Giả sử un là số hạng thứ n của cấp số cộng thứ nhất ta có: un = 5 + 3(n – 1)
và vm = 3 + 4(m – 1) là số hạng thứ m của cấp số cộng thứ 2.
Để un = vm khi và chỉ khi:
5 + 3(n - 1) = 3 + 4(m - 1) hay 3n + 2 = 4m - 1 ⇒ n = m/3 + m – 1
Đặt m/3 = t (t ∈ N*) ⇒ m = 3t; n= 4t - 1
Vì m; n không lớn hơn 100 nên:
Kết hợp với t là số nguyên dương nên t ∈ {1; 2; 3;…; 25}
Tương ứng với 25 giá trị của t ta được 25 số hạng chung của 2 dãy (un); (vm).
Câu 19:
23/07/2024Cho cấp số cộng có công sai d = 1 và u22 – 2u32 – u42 đạt giá trị lớn nhất. Tính tổng S20 của 20 số hạng đầu tiên của cấp số cộng đó.
Xem đáp án
Chọn C.
Dấu bằng xảy ra khi a + 3 = 0 hay a = -3.
Suy ra u1 = -3.
Ta có 
.
Câu 20:
17/07/2024Cho tam giác ABC có độ dài các cạnh là a; b; c theo thứ tự lập thành một cấp số cộng. Biết , giá trị x + y là:
Xem đáp án
Chọn A.
Do đó x + y = 4.
Câu 21:
19/07/2024Cho dãy số xác định bởi a1 = 1; an+1 = 3an + 10. Tìm số hạng thứ 15 của dãy số (an).
Xem đáp án
Chọn A.
Chúng ta đi tìm công thức xác định số hạng tổng quát của dãy số (an).
Đặt bn = an + 5 khi đó bn+1 = an+1 + 5.
Từ hệ thức truy hồi an+1 = 3an + 10 suy ra bn+1 – 5 = 3(bn – 5) + 10 ⇔ bn+1 = 3bn.
Suy ra, dãy số là cấp số nhân với số hạng đầu là b1 = a1 + 5 = 6; công bội q = 3
Do đó, , ∀ n ∈ N*,
suy ra an = 6.3n-1 – 5, ∀ n ∈ N*.
Do đó a15 = 28697809.
Câu 22:
22/07/2024Dãy số (un) xác định bởi (n dấu căn). Khẳng định nào sau đây là đúng?
Xem đáp án
Chọn A.
Ta có un+12 = 2010 + un ⇒ un+1 – un = -un+12 + un+1 + 2010
Bằng quy nạp ta chứng minh được 
Suy ra un+1 – un > 0 ⇒ dãy (un) là dãy tăng.
Câu 23:
21/07/2024Cho dãy số (un) được xác định như sau: Viết 4 số hạng đầu của dãy và chứng minh rằng un > 0, ∀ n
Xem đáp án
Chọn B.
Ta có: u1 = 1; u2 = 3/2; u3 = 17/6; u4 = 227/34.
Ta chứng minh un > 0 bằng quy nạp.
Giả sử un > 0, khi đó: 
Nên 
.
Câu 24:
23/07/2024Cho dãy số (un) được xác định bởi : . Khẳng định nào sau đây đúng
Xem đáp án
Chọn A.
Từ công thức truy hồi, ta suy ra: ( chứng minh bằng phương pháp quy nạp)
Ta có: 
nên dãy (un) là dãy giảm.
Câu 25:
21/07/2024Cho dãy số (un) được xác định bởi : Tìm phần nguyên của (un) với 0 ≤ n ≤ 1006.
Xem đáp án
Chọn B.
Từ công thức truy hồi, và bằng phương pháp quy nạp ta chứng minh được
Ta có: 
Suy ra: un > u0 – n = 2011 – n
Mặt khác: un = (un – un-1) + (un-1 – un-2) + … + (u1 – u0) + u0
Mà:
Suy ra un < u0 – n + 1 = 2012 – n
Do đó: 2011 – n < un < 2012 – n ⇒ [un] = 2011 – n
Vì u0 = 2011 và 
nên [u0] = 2011 – 0, [u1] = 2010 = 2011 – 1
Vậy [un] = 2011 – n, 