Nội dung bài viết

    Xem thêm

    Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = (x + 3)/(x + 1)

    Với giải bài tập 11 trang 46 sgk Toán lớp 12 Giải tích được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

    1 5,653 15/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Bài 6: Ôn tập chương 1

    Bài 11 trang 46 Toán lớp 12 Giải tích:

    a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y=x+3x+1.

    b) Chứng minh rằng với mọi giá trị của m, đường thẳng y = 2x + m luôn cắt (C) tại hai điểm phân biệt M và N.

    c) Xác định m sao cho độ dài MN nhỏ nhất.

    d) Tiếp tuyến tại một điểm S bất kì của (C) cắt hai tiệm cận của (C) tại P và Q. Chứng minh rằng S là trung điểm của PQ.

    Lời giải:

    a) Khảo sát hàm số y=x+3x+1.

    - TXĐ: D = ℝ \ {-1}

    - Sự biến thiên:

    + Chiều biến thiên:

    y'=−2x+12<0     ∀x∈D

    Suy ra hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞).

    + Cực trị: Hàm số không có cực trị.

    + Tiệm cận:

    limx→−1−x+3x+1=−∞;limx→−1+x+3x+1=+∞

    Suy ra x = -1 là tiệm cận đứng của đồ thị hàm số.

    Lại có: 

    limx→±∞x+3x+1=limx→±∞1+3x1+1x=1

    Suy ra y = 1 là tiệm cận ngang của đồ thị hàm số.

    + Bảng biến thiên:

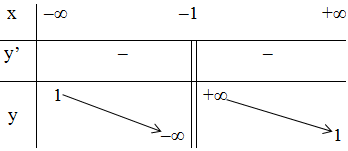
    Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (ảnh 1)

    - Đồ thị:

    + Giao với Ox: (-3; 0)

    + Giao với Oy: (0; 3)

    + Đồ thị hàm số nhận (-1; 1) là tâm đối xứng.

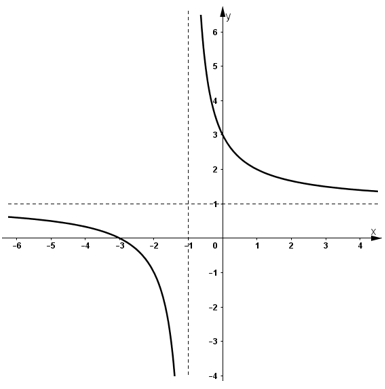
    Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (ảnh 1)

    b) Phương trình hoành độ giao điểm của (C) và đường thẳng (d) y = 2x + m là: x+3x+1=2x+m

    ⇔x+3=2x+mx+1     1x≠−1

    Ta có:

    (1)⇔(2x + m)(x + 1) = x + 3

    ⇔2x2 + mx + 2x + m = x + 3

    ⇔ 2x2 + (m + 1)x + m – 3 = 0 (*)

    Ta có:

    2 . (-1)2 + (m + 1) . (-1) + m – 3

    = 2 – m – 1 + m – 3 = - 2 ≠ 0

    nên x = - 1 không phải là nghiệm của (*)

    Để (d) cắt (C) tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt.

    ⇔ Δ = (m + 1)2 – 8(m – 3) > 0

    ⇔m2 – 6m + 25 > 0

    ⇔ (m – 3)2 + 16 > 0

    Đúng với mọi m∈ℝ.

    Vậy với mọi m∈ℝ, (d) cắt (C) tại hai điểm phân biệt M và N.

    c) Gọi M(xM; yM); N(xN; yN)

    Suy ra xM; xN là nghiệm của phương trình (*).

    Theo hệ thức Vi-et ta có :

    xM+xN=−m+12xM.xN=m−32

    Ta có:

    MN2=xM−xN2+yM−yN2=xM−xN2+2xM+m−2xN−m2=5xM−xN2=5xM+xN2−20xM.xN=5.−m+122−20.m−32=54m2−152m+1254=54m2−6m+9+20=54m−32+20≥20  ∀m

    Dấu "=" xảy ra⇔m - 3 = 0⇔m = 3

    Vậy độ dài MN nhỏ nhất khi m = 3.

    d) Gọi Sx0;x0+3x0+1 là một điểm thuộc (C).

    Ta có: y'x0=−2x0+12

    + Phương trình tiếp tuyến (d) của (C) tại S là:

    y=−2x0+12x−x0+x0+3x0+1

    + Giao điểm của (d) với tiệm cận đứng x = -1:

    Tại x = -1 thì  

    y=−2x0+12−1−x0+x0+3x0+1

    Suy ra giao điểm P−1;x0+5x0+1

    + Giao điểm của (d) với tiệm cận ngang y = 1:

    Tại y = 1

    ⇒−2x0+12x−x0+x0+3x0+1=1

    ⇒x=2x0+1

    Suy ra giao điểm Q(2x0 + 1; 1)

    Ta có:

    xP+xQ=−1+2x0+1=2x0=2xSyP+yQ=x0+5x0+1+1=2x0+6x0+1=2.x0+3x0+1=2yS

    Vậy S là trung điểm PQ (đpcm).

    Xem thêm lời giải bài tập Toán lớp 12 hay, chi tiết khác:

    Bài 1 trang 45 Toán 12 Giải tích: Phát biểu các điều kiện đồng biến và nghịch biến của hàm số...

    Bài 2 trang 45 Toán 12 Giải tích: Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm...

    Bài 3 trang 45 Toán 12 Giải tích: Nêu cách tìm ra tiệm cận ngang và tiệm cận đứng của đồ thị hàm số...

    Bài 4 trang 45 Toán 12 Giải tích: Nhắc lại sơ đồ khảo sát sự biến thiên và vẽ đồ thị của hàm số...

    Bài 5 trang 45 Toán 12 Giải tích: Cho hàm số y = 2x2 + 2mx + m - 1 có đồ thị là (Cm), m là tham số...

    Bài 6 trang 45 Toán 12 Giải tích: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số...

    Bài 7 trang 45, 46 Toán 12 Giải tích: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = x3 + 3x2 + 1...

    Bài 8 trang 46 Toán 12 Giải tích: Cho hàm số f(x) = x3 - 3mx2 + 3(2m - 1)x + 1 (m là tham số)...

    Bài 9 trang 46 Toán 12 Giải tích: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ...

    Bài 10 trang 46 Toán 12 Giải tích: Cho hàm số y = -x4 + 2mx2 - 2m + 1 (m tham số) có đồ thị là (Cm)...

    Bài 12 trang 47 Toán 12 Giải tích: Cho hàm số ...

    Bài 1 trang 47 Toán 12 Giải tích: Số điểm cực trị của hàm số  là...

    Bài 2 trang 47 Toán 12 Giải tích: Số điểm cực đại của hàm số y = x4 + 100 là...

    Bài 3 trang 47 Toán 12 Giải tích: Số đường tiệm cận của đồ thị hàm số là...

    Bài 4 trang 47 Toán 12 Giải tích: Hàm số  đồng biến trên...

    Bài 5 trang 47 Toán 12 Giải tích: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số ...

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 5,653 15/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: