Giải SBT Toán 10 trang 81 Tập 1 Chân trời sáng tạo
Với Giải SBT Toán 10 trang 81 Tập 1 trong Bài tập cuối chương 4 Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 81.
Giải SBT Toán 10 trang 81 Tập 1 Chân trời sáng tạo
Bài 9 trang 81 SBT Toán 10 Tập 1: Tam giác ABC có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
A. 2S;
B. 3S;
C. 4S;
D. 6S.
Lời giải
Đáp án đúng là D
Diện tích tam giác ABC ban đầu là: S = . BC.AC.sinC
Diện tích tam giác ABC lúc sau là: Ss = .2BC.3AC.sinC = 6. . BC.AC.sinC = 6S.
Vậy đáp án đúng là D.
Bài 10 trang 81 SBT Toán 10 Tập 1: Cho = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
A. 1,5;
B. ;
C. ;
D. 2.
Lời giải
Đáp án đúng là D
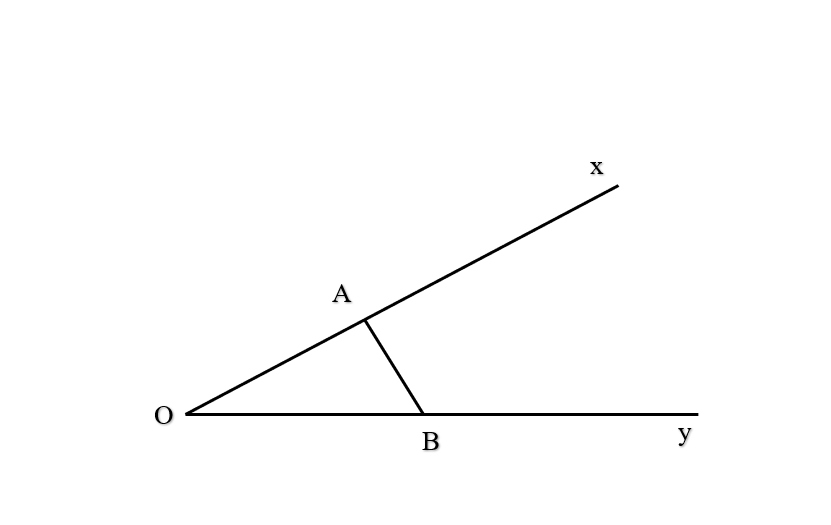
Theo định lí sin ta có:
OB = 2sin.
Ta có –1 ≤ sin≤ 1 nên OB lớn nhất khi sin = 1 ⟺ = 90°.
Khi đó OB = 2.
Đáp án đúng là D.
B. Tự luận
Bài 1 trang 81 SBT Toán 10 Tập 1: Cho tam giác ABC với ba cạnh a, b, c. Chứng minh rằng: .
Lời giải
Theo định lí côsin: a2 = b2 + c2 – 2bccosA
⇒ cosA =
⇒ = .
Tương tự ta có:
= và =
Như vậy: = + +
⇒ . ( ĐPCM ).
Bài 2 trang 81 SBT Toán 10 Tập 1: Cho tam giác ABC. Biết a = 24; b = 36; = 52°. Tính cạnh c và hai góc
Lời giải
Áp dụng định lí côsin ta có:
c2 = a2 + b2 – 2abcos![]()
c2 = 242 + 362 – 2.24.36.cos52°
c =
c ≈ 28,43.
Áp dụng định lí sin ta có:
=
⇒ sinA = a : = 24 : ≈ 0,665 ⇒ ≈ 41°40’56’’.
⇒ sinB = b : = 36 : ≈ 0,998 ⇒ ≈ 86°22’32’’.
Vậy ≈ 41°40’56’’ và ≈ 86°22’32’’.
Bài 3 trang 81 SBT Toán 10 Tập 1: Hai chiếc tàu thủy P và Q cách nhau 50 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc = 40° và = 52°. Tính chiều cao của tháp hải đăng đó.
Lời giải
Ta có hình vẽ sau:
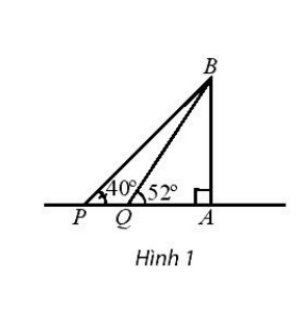
Ta có: = 40°, = 52°, = 90°, PQ = 50 m.
là góc kề bù với ⇒ = 180° – 52° = 128°
Xét tam giác PBQ: + + = 180°
⇒ = 180° – 128° – 40° = 12°.
Áp dụng định lí sin cho tam giác PBQ ta có:
= ⇒ BQ = . sinP = .sin40° ≈ 154,58 m.
Xét tam giác ABQ vuông tại A: AB = BQ. sin52° = 154,58. sin52° ≈ 121,81 m.
Vậy chiều cao của tháp hải đăng khoảng 121,81 m.
Bài 4 trang 81 SBT Toán 10 Tập 1: Cho tam giác ABC có = 99°, b = 6, c = 10. Tính:
a) Diện tích tam giác ABC;
b) Bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC.
Lời giải
a) Diện tích tam giác ABC là:
S = .b.c.sin= .6.10.sin99° ≈ 29,63 (đvdt).
Vậy diện tích tam giác ABC là 29,63 đvdt.
b) Áp dụng định lí côsin ta có:
a2 = b2 + c2 – 2bccosA
a2 = 62 + 102 – 2.6.10.cos99°
a =
a ≈ 12,44.
Áp dụng định lí sin ta có:
⇒ R = = ≈ 6,30.
Nửa chu vi tam giác ABC là: p = .
Lại có: r = = ≈ 2,08.
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 6,30 và bán kính đường tròn nội tiếp tam giác ABC là 2,08.
Bài 5 trang 81 SBT Toán 10 Tập 1: Hai máy bay rời một sân bay cùng một lúc. Một chiếc máy bay với vận tốc 800 km/h theo hướng lệch so với hướng bắc 15° về phía tây. Chiếc còn lại bay theo hướng lệch so với hướng nam 45° về phía tây với vận tốc 600 km/h ( Hình 1). Hỏi hai máy bay đó cách nhau bao xa sau 3 giờ?
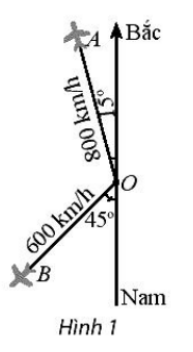
Lời giải
Ta có hình vẽ sau:
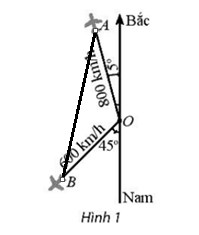
Ta có: = 180° – 15° – 45° = 120°.
Sau 3 giờ hai máy bay bay từ O đến A đi được quãng đường là: 800.3 = 2 400 km.
Hay OA = 2 400.
Sau 3 giờ hai máy bay bay từ O đến B đi được quãng đường là: 600.3 = 1 800 km.
Hay OB = 1 800.
Sau 3 giờ, hai máy bay A, B và điểm xuất phát O tạo thành tam giác OAB với OA = 2400 và OB = 1800. Áp dụng định lí côsin cho tam giác OAB ta được:
AB2 = OA2 + OB2 – 2.OA.OB.cos
AB2 = 24002 + 18002 – 2.1800.2400.cos120°
AB =
AB ≈ 3650 km
Vậy sau 3 giờ hai máy bay cách nhau khoảng 3650 km.
Bài 6 trang 81 SBT Toán 10 Tập 1: Cho tam giác ABC không vuông. Chứng minh rằng:
.
Lời giải
Theo định lí côsin ta có: a2 = b2 + c2 – 2bcosA
⇒ cosA =
Tương tự: cosB =
Theo định lí côsin ta có:
⇒ sinA = và sinB =
Ta có:
=... = (ĐPCM).
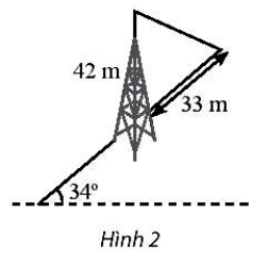
Bài 7 trang 81 SBT Toán 10 Tập 1: Một tháp viễn thông cao 42 m được dựng thẳng đứng trên một sườn dốc 34° so với phương ngang. Từ đỉnh tháp người ta neo một sợi cáp xuống một điểm trên sườn dốc cách chân tháp 33 m như Hình 2. Tính chiều dài của sợi dây cáp đó.
Lời giải
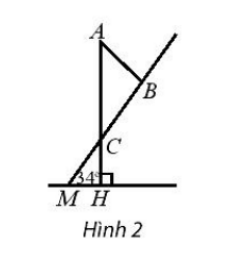
Ta biểu diễn lại hình như trên. AB là độ dài sợi dây cáp. AC là độ dài tháp. Như vậy AC = 42 m, BC = 33 m, = 34°, = 90°.
Xét tam giác MCH: = 180°.
⇒ = 180° – 90° – 34° = 56°.
và là hai góc đối đỉnh nên = 56° ( tính chất hai góc đối đỉnh).
Áp dụng định lí côsin cho tam giác ABC:
AB2 = AC2 + BC2 – 2.AC.BC.cos
AB2 = 422 + 332 – 2.42.33.cos56°
AB =
AB ≈ 36,1 m
Vậy chiều dài sợi dây cáp khoảng 36,1 m.
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Giải SBT Toán 10 trang 80 Tập 1
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Giá trị lượng giác của 1 góc từ 0° đến 180°
Bài 2: Định lí côsin và định lí sin
Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Soạn văn lớp 10 (ngắn nhất) – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Giải sbt Ngữ văn lớp 10 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Văn mẫu lớp 10 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 10 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Giải sbt Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 10 Friends Global đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 Friends Global
- Giải sgk Vật lí 10 – Chân trời sáng tạo
- Giải sbt Vật lí 10 – Chân trời sáng tạo
- Lý thuyết Vật lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Vật lí 10 – Chân trời sáng tạo
- Giải sgk Hóa học 10 – Chân trời sáng tạo
- Lý thuyết Hóa học 10 – Chân trời sáng tạo
- Giải sbt Hóa học 10 – Chân trời sáng tạo
- Giải Chuyên đề Hóa học 10 – Chân trời sáng tạo
- Giải sgk Sinh học 10 – Chân trời sáng tạo
- Giải sbt Sinh học 10 – Chân trời sáng tạo
- Lý thuyết Sinh học 10 – Chân trời sáng tạo
- Giải Chuyên đề Sinh học 10 – Chân trời sáng tạo
- Giải sgk Lịch sử 10 – Chân trời sáng tạo
- Giải sbt Lịch sử 10 – Chân trời sáng tạo
- Giải Chuyên đề Lịch sử 10 – Chân trời sáng tạo
- Lý thuyết Lịch sử 10 – Chân trời sáng tạo
- Giải sgk Địa lí 10 – Chân trời sáng tạo
- Lý thuyết Địa Lí 10 - Chân trời sáng tạo
- Giải sbt Địa lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Địa lí 10 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải Chuyên đề Kinh tế và pháp luật 10 – Chân trời sáng tạo
- Lý thuyết KTPL 10 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 10 – Chân trời sáng tạo
