Nội dung bài viết

    Xem thêm

    Giải SBT Toán 10 trang 19 Tập 2 Chân trời sáng tạo

    Với Giải SBT Toán 10 trang 19 Tập 2 trong Bài 3: Phương trình quy về phương trình bậc hai Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 19.

    1 211 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 trang 19 Tập 2 Chân trời sáng tạo

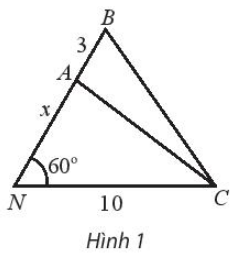
    Bài 5 trang 19 SBT Toán 10 Tập 2: Khoảng cách từ nhà An ở vị trí N đến cột điện C là 10 m. Từ nhà, An đi x mét theo phương tạo với NC một góc 60° đến vị trí A sau đó đi tiếp 3m đến vị trí B như Hình 1.

    a) Biểu diễn khoảng cách AC và BC theo x.

    b) Tìm x để AC=89BC

    c) Tìm x để khoảng cách BC = 2AN.

    Sách bài tập Toán 10 Bài 3: Phương trình quy về phương trình bậc hai - Chân trời sáng tạo (ảnh 1)

    Lưu ý: Đáp số làm tròn đến hàng phần mười.

    Lời giải:

    a) Vì x là khoảng cách AN nên x > 0

    Áp dụng định lí côsin cho tam giác ANC:

    AC2 = AN2 + NC2 – 2.AN.NC.cos60°

    AC2 = x2 + 100 – 2.x.10.12 = x2 – 10x + 100

    Như vậy AC = x2– 10x + 100

    Áp dụng định lí côsin cho tam giác BNC:

    BC2 = BN2 + NC2 – 2.AN.NC.cos60°

    BC2 = ( 3 + x )2 + 100 – 2.( 3 + x ).10.12 = x2 + 6x + 9 + 100 – 30 – 10x

    BC2  = x2 – 4x + 79

    Như vậy BC = x2– 4x + 79.

    b) Ta có AC=89BC 

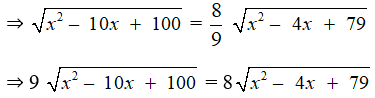
    Sách bài tập Toán 10 Bài 3: Phương trình quy về phương trình bậc hai - Chân trời sáng tạo (ảnh 1)

    ⇒ 81( x2 – 10x + 100 ) = 64( x2 – 4x + 79 )

    ⇒ 17x2 – 554x + 3044 = 0

    ⇒ x ≈ 25,6 hoặc x ≈ 7

    Vậy x ≈ 25,6 hoặc x ≈ 7.

    c) Ta có BC = 2AN

    ⇒ x2– 4x + 79 = 2x

    ⇒ x2 – 4x + 79 = 4x2

    ⇒ 3x2 + 4x – 79 = 0

    ⇒ x ≈ 4,5 hoặc x ≈ –5,8 mà x > 0 nên x ≈ 4,5.

    Vậy x ≈ 4,5 .

    Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải SBT Toán 10 trang 18 Tập 2

    Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

    Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

    Bài tập cuối chương 6

    Bài 1: Dấu của tam thức bậc hai

    Bài 2: Giải bất phương trình bậc hai một ẩn

    Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Lý thuyết Bài 3: Phương trình quy về phương trình bậc hai

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 211 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: