Chuyên đề Toán 10 (Chân trời sáng tạo) Bài tập cuối chuyên đề 2

Giải bài tập Chuyên đề Toán 10 Bài tập cuối chuyên đề 2

Giải bài tập trang 40 Chuyên đề Toán 10 Bài tập cuối chuyên đề 2

Bài 1 trang 40 Chuyên đề Toán 10:

Chứng minh rằng các đẳng thức sau đúng với mọi $n\in {\mathbb{N}}^{*}$.

a) $1^3+2^3+3^3+\dots +n^3=\frac{n^2{(n+1)}^2}{4}$;

b) $1.4+2.7+3.10+\dots +$$n(3n+1)=n{(n+1)}^2$;

c) $\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\dots$$+\frac{1}{(2n-1)(2n+1)}=\frac{n}{2n+1}$.

Lời giải:

a) Bước 1. Với n = 1, ta có 1³ = $\frac{1^2{\left(1+1\right)}^2}{4}.$ Do đó đẳng thức đúng với n = 1.

Bước 2. Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

$1^3+2^3+3^3+\dots +k^3$$=\frac{k^2{(k+1)}^2}{4}.$

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

$$\begin{gathered} 1^3+2^3+3^3+\dots +k^3+{\left(k+1\right)}^3 \\ =\frac{{\left(k+1\right)}^2{\left[(k+1)+1\right]}^2}{4}. \end{gathered}$$

Sử dụng giả thiết quy nạp, ta có:

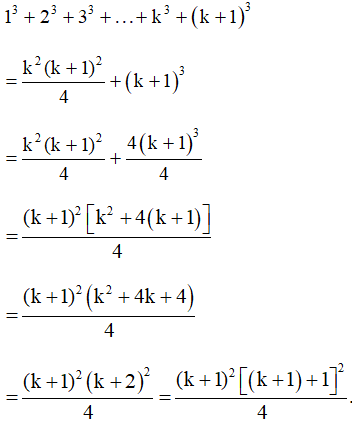
Vậy đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

b) Bước 1. Với n = 1, ta có 1(3 . 1 + 1) = 4 = 1(1 +  1)². Do đó đẳng thức đúng với n = 1.

Bước 2. Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

$$\begin{gathered} 1.4+2.7+3.10+\dots +k(3k+1) \\ =k{(k+1)}^2. \end{gathered}$$

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

$1.4+2.7+3.10+\dots +k(3k+1)+$$\left(k+1\right)\left[3\left(k+1\right)+1\right]=\left(k+1\right){\left[(k+1)+1\right]}^2.$

Sử dụng giả thiết quy nạp, ta có:

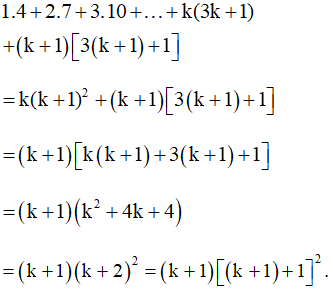
Vậy đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

c) Bước 1. Với n = 1, ta có $\frac{1}{(2.1-1)(2.1+1)}$$=\frac{1}{3}=\frac{1}{2.1+1}.$ Do đó đẳng thức đúng với n = 1.

Bước 2. Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

$\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\dots +$$\frac{1}{(2k-1)(2k+1)}=\frac{k}{2k+1}.$

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

$\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\dots +$$\frac{1}{(2k-1)(2k+1)}+$$\frac{1}{\left[2\left(k+1\right)-1\right]\left[2\left(k+1\right)+1\right]}$$=\frac{k+1}{2\left(k+1\right)+1}.$

Sử dụng giả thiết quy nạp, ta có:

$\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\dots +\frac{1}{(2k-1)(2k+1)}$$+\frac{1}{\left[2\left(k+1\right)-1\right]\left[2\left(k+1\right)+1\right]}$

$=\frac{k}{2k+1}+\frac{1}{\left[2\left(k+1\right)-1\right]\left[2\left(k+1\right)+1\right]}$

$=\frac{k}{2k+1}+\frac{1}{\left(2k+1\right)\left(2k+3\right)}$

$=\frac{k\left(2k+3\right)+1}{\left(2k+1\right)\left(2k+3\right)}$

$=\frac{2k^2+3k+1}{\left(2k+1\right)\left(2k+3\right)}$

$$\begin{gathered} =\frac{\left(k+1\right)\left(2k+1\right)}{\left(2k+1\right)\left(2k+3\right)} \\ =\frac{k+1}{2k+3}=\frac{k+1}{2\left(k+1\right)+1}. \end{gathered}$$

Vậy đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

Bài 2 trang 40 Chuyên đề Toán 10:

Chứng minh rằng với mọi n $\in {\mathbb{N}}^{*}$:

a) 3ⁿ – 1 – 2n chia hết cho 4;

b) 7ⁿ – 4ⁿ – 3ⁿ chia hết cho 12.

Lời giải:

a) Bước 1. Với n = 1, ta có 3¹ – 1 – 2 . 1 = 0 ⁝ 4. Do đó khẳng định đúng với n = 1.

Bước 2. Giả sử khẳng định đúng với n = k ≥ 1, nghĩa là có: 3^k – 1 – 2k ⁝ 4.

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

3^{k + 1} – 1 – 2(k + 1) ⁝ 4.

Sử dụng giả thiết quy nạp, ta có:

3^{k + 1} – 1 – 2(k + 1) = 3 . 3^k – 1 –2k – 2 = 3 . 3^k – 3 –2k = 3 . 3^k – 3 –6k + 4k

= 3(3^k – 1 – 2k) + 4k

Vì (3^k – 1 – 2k) và 4k đều chia hết cho 4 nên 3(3^k – 1 – 2k) + 4k ⁝ 4 hay 3^{k + 1} – 1 – 2(k + 1) ⁝ 4.

Vậy khẳng định đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, khẳng định đúng với mọi số tự nhiên n ≥ 1.

b) Bước 1. Với n = 1, ta có 7¹ – 4¹ – 3¹ = 0 ⁝ 12. Do đó khẳng định đúng với n = 1.

Bước 2. Giả sử khẳng định đúng với n = k ≥ 1, nghĩa là có: 7^k – 4^k – 3^k ⁝ 12.

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

7^{k + 1} – 4^{k + 1} – 3^{k + 1} ⁝ 12.

Sử dụng giả thiết quy nạp, ta có:

7^{k + 1} – 4^{k + 1} – 3^{k + 1} = 7 . 7^k – 4 . 4^k – 3 . 3^k = 7 . 7^k – 7 . 4^k – 7 . 3^k + 3 . 4^k + 4 . 3^k

= 7(7^k – 4^k – 3^k) + 3 . 4^k + 4 . 3^k = 7(7^k – 4^k – 3^k) + 12 . 4^{k – 1} + 12 . 3^{k – 1} (vì k ≥ 1).

Vì 7(7^k – 4^k – 3^k), 12 . 4^{k – 1} và 12 . 3^{k – 1} đều chia hết cho 12 nên 7(7^k – 4^k – 3^k) + 12 . 4^{k – 1} + 12 . 3^{k – 1} ⁝ 12 hay 7^{k + 1} – 4^{k + 1} – 3^{k + 1} ⁝ 12.

Vậy khẳng định đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, khẳng định đúng với mọi số tự nhiên n ≥ 1.

Bài 3 trang 40 Chuyên đề Toán 10: Chứng minh rằng 8ⁿ ≥ n³ với mọi n $\in {\mathbb{N}}^{*}$.

Lời giải:

Bước 1. Với n = 1, ta có 8¹ = 8 > 1 = 1³. Do đó bất đẳng thức đúng với n = 1.

Bước 2. Giả sử bất đẳng thức đúng với n = k ≥ 1, nghĩa là có: 8^k ≥ k³.

Ta cần chứng minh bất đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

8^{k + 1} ≥ (k + 1)³.

Sử dụng giả thiết quy nạp, ta có:

8^{k + 1} = 8 . 8^k ≥ 8 . k³ = k³ + 3k³ + 3k³ + k³ ≥ k³ + 3k² + 3k + 1 (vì k ≥ 1) = (k + 1)³.

Vậy bất đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, bất đẳng thức đúng với mọi số tự nhiên n ≥ 1.

Bài 4 trang 40 Chuyên đề Toán 10: Chứng minh rằng bất đẳng thức $1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}\le \frac{n+1}{2}$ đúng với mọi $n\in {\mathbb{N}}^{*}$.

Lời giải:

Bước 1. Với n = 1, ta có $\frac{1}{1}=1=\frac{1+1}{2}.$ Do đó bất đẳng thức đúng với n = 1.

Bước 2. Giả sử bất đẳng thức đúng với n = k ≥ 1, nghĩa là có:

$1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{k}\le \frac{k+1}{2}.$

Ta cần chứng minh bất đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

$1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{k}+\frac{1}{k+1}$$\le \frac{\left(k+1\right)+1}{2}.$

Sử dụng giả thiết quy nạp, ta có:

$1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{k}+\frac{1}{k+1}\le$$\frac{k+1}{2}+\frac{1}{k+1}=$$\frac{{\left(k+1\right)}^2+2}{2\left(k+1\right)}=\frac{k^2+2k+3}{2\left(k+1\right)}$

$\le \frac{k^2+2k+1+2}{2\left(k+1\right)}\le \frac{k^2+2k+k+2}{2\left(k+1\right)}$$=\frac{k^2+3k+2}{2\left(k+1\right)}=\frac{\left(k+1\right)\left(k+2\right)}{2\left(k+1\right)}$$=\frac{k+2}{2}=\frac{\left(k+1\right)+1}{2}.$

Vậy bất đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, bất đẳng thức đúng với mọi số tự nhiên n ≥ 1.

Bài 5 trang 40 Chuyên đề Toán 10: Với một bình rỗng có dung tích 2 l, một bạn học sinh thực hiện thí nghiệm theo các bước như sau:

Bước 1: Rót 1 l nước vào bình, rồi rót đi một nửa lượng nước trong bình.

Bước 2: Rót 1 l nước vào bình, rồi lại rót đi một nửa lượng nước trong bình.

Cứ như vậy, thực hiện các bước 3,4,...

Kí hiệu a_n là lượng nước có trong bình sau bước $n\left(n\in {\mathbb{N}}^{*}\right)$.

a) Tính a₁, a₂, a₃. Từ đó dự đoán công thức tính a_n với n $\left(n\in {\mathbb{N}}^{*}\right)$

b) Chứng minh công thức trên bằng phương pháp quy nạp toán học.

Lời giải:

a) Sau bước 1 thì trong bình có $\frac{1}{2}$ l nước, do đó a₁ = $\frac{1}{2}$

Sau bước 2 thì trong bình có: $\frac{\left(\frac{1}{2}+1\right)}{2}=\frac{3}{4}$ l nước, do đó a₂ = $\frac{3}{4}$

Sau bước 3 thì trong bình có: $\frac{\left(\frac{3}{4}+1\right)}{2}=\frac{7}{8}.$ l nước, do đó a₂ = $\frac{7}{8}$

Ta có thể dự đoán a_n = $\frac{2^n-1}{2^n}.$

b) Ta chứng minh bằng quy nạp:

Bước 1. Với n = 1, ta có a₁ = $\frac{1}{2}=\frac{2^1-1}{2^1}.$ Do đó công thức đúng với n = 1.

Bước 2. Giả sử công thức đúng với n = k ≥ 1, nghĩa là có: a_k = $\frac{2^k-1}{2^k}.$

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

a_{k + 1} = $\frac{2^{k+1}-1}{2^{k+1}}.$

Thật vậy:

a_k là lượng nước có trong bình sau bước thứ k thì lượng nước có trong bình sau bước thứ k + 1 là:

a_{k + 1} = $\frac{a_k+1}{2}$

$$\begin{gathered} =\frac{\frac{2^k-1}{2^k}+1}{2}=\frac{\frac{\left(2^k-1\right)+2^k}{2^k}}{2} \\ =\frac{2.2^k-1}{2^k.2}=\frac{2^{k+1}-1}{2^{k+1}}. \end{gathered}$$

Vậy công thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, công thức đúng với mọi số tự nhiên n ≥ 1.

Bài 6 trang 40 Chuyên đề Toán 10:

Tìm hệ số của x³ trong khai triển:

a) (1 – 3x)⁸;

b) ${\left(1+\frac{x}{2}\right)}^7$.

Lời giải:

a) Áp dụng công thức nhị thức Newton, ta có:

(1 – 3x)⁸ = $C_8^0{1}^8+C_8^1{1}^7\left(-3x\right)+\mathrm{...}+$$C_8^k{1}^{8-k}{\left(-3x\right)}^k+\mathrm{...}+C_8^8{\left(-3x\right)}^8$

$=1+C_8^1\left(-3\right)x+\mathrm{...}+$$C_8^k{\left(-3\right)}^k{x}^k+\mathrm{...}+C_8^8{\left(-3\right)}^8{x}^8.$

Số hạng chứa x³ ứng với giá trị k = 3. Hệ số của số hạng này là $C_8^3{\left(-3\right)}^3=-1512.$

b) Áp dụng công thức nhị thức Newton, ta có:

${\left(1+\frac{x}{2}\right)}^7$ = $C_7^0{1}^7+C_7^1{1}^6\left(\frac{x}{2}\right)+\mathrm{...}+$$C_7^k{1}^{7-k}{\left(\frac{x}{2}\right)}^k+\mathrm{...}+C_7^7{\left(\frac{x}{2}\right)}^7$

$=1+C_7^1\frac{1}{2}x+\mathrm{...}+$$C_7^k{\left(\frac{1}{2}\right)}^k{x}^k+\mathrm{...}+C_7^7{\left(\frac{1}{2}\right)}^7{x}^7.$

Số hạng chứa x³ ứng với giá trị k = 3. Hệ số của số hạng này là $C_7^3{\left(\frac{1}{2}\right)}^3=\frac{35}{8}.$

Bài 7 trang 40 Chuyên đề Toán 10:

Tìm hệ số của x⁵ trong khai triển (2x + 3)(x – 2)⁶.

Lời giải:

Có (2x + 3)(x – 2)⁶

= 2x(x – 2)⁶ + 3(x – 2)⁶.

Ta tìm hệ số của x⁵ trong từng khai triển: 2x(x – 2)⁶ và 3(x – 2)⁶.

+) Có: 2x(x – 2)⁶

= 2x$\text{[}{C}_6^0{x}^6+C_6^1{x}^5\left(-2\right)+$$C_6^2{x}^4{\left(-2\right)}^2+C_6^3{x}^3{\left(-2\right)}^3$

$+C_6^4{x}^2{\left(-2\right)}^4+C_6^{5}x{\left(-2\right)}^5+C_6^6{\left(-2\right)}^6\text{]}$

= $2C_6^0{x}^7+2\left(-2\right)C_6^1{x}^6+$$2{\left(-2\right)}^2{C}_6^2{x}^5+2{\left(-2\right)}^3{C}_6^3{x}^4$

$+2{\left(-2\right)}^4{C}_6^4{x}^3+$$2{\left(-2\right)}^5{C}_6^5{x}^2+2{\left(-2\right)}^6{C}_6^{6}x.$

Hệ số của x⁵ trong khai triển này là 2(–2)²$C_6^2$ = 120.

+) Có: 3(x – 2)⁶

= 3$\text{[}{C}_6^0{x}^6+C_6^1{x}^5\left(-2\right)+$$C_6^2{x}^4{\left(-2\right)}^2+C_6^3{x}^3{\left(-2\right)}^3$

$+C_6^4{x}^2{\left(-2\right)}^4+C_6^{5}x{\left(-2\right)}^5+C_6^6{\left(-2\right)}^6\text{]}$

$=3C_6^0{x}^6+3\left(-2\right)C_6^1{x}^5+$$3{\left(-2\right)}^2{C}_6^2{x}^4+3{\left(-2\right)}^3{C}_6^3{x}^3$

$+3{\left(-2\right)}^4{C}_6^4{x}^2+$$3{\left(-2\right)}^5{C}_6^{5}x+3{\left(-2\right)}^6{C}_6^6.$

Hệ số của x⁵ trong khai triển này là $3\left(-2\right)C_6^1$ = –36.

Vậy hệ số của x⁵ trong khai triển (2x + 3)(x – 2)⁶ là 120 + (–36) = 84.

Bài 8 trang 40 Chuyên đề Toán 10:

a) Tìm ba số hạng đầu tiên trong khai triển của (1 + 2x)⁶, các số hạng được viết theo thứ tự số mũ của x tăng dần.

b) Sử dụng kết quả trên, hãy tính giá trị gần đúng của 1,02⁶.

Lời giải:

a) Sử dụng tam giác Pascal, ta có:

(1 + 2x)⁶

$$\begin{gathered} =1^6+{6.1}^5\left(2x\right)+{15.1}^4{\left(2x\right)}^2+{20.1}^3{\left(2x\right)}^3 \\ +{15.1}^2{\left(2x\right)}^4+6.1{\left(2x\right)}^5+{\left(2x\right)}^6 \end{gathered}$$

$=1+12x+60x^2+160x^3$$+240x^4+192x^5+64x^6.$

Ba số hạng đầu tiên của khai triển là 1, 12x và 60x².

b) Với x nhỏ thì x³, x⁴, x⁵, x⁶ sẽ rất nhỏ. Do đó có thể coi (1 + 2x)⁶ ≈ 1 + 12x + 60x².

Khi đó 1,02⁶ = (1 + 2 . 0,01)⁶ ≈ 1 + 12 . 0,01 + 60 . 0,01² = 1,126.

Bài 9 trang 40 Chuyên đề Toán 10:

Trong khai triển biểu thức (3x – 4)¹⁵ thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.

Lời giải:

Có (3x – 4)¹⁵

$=C_{15}^0{\left(3x\right)}^{15}+C_{15}^1{\left(3x\right)}^{14}\left(-4\right)+\mathrm{...}+$$C_{15}^k{\left(3x\right)}^{15-k}{\left(-4\right)}^k+\mathrm{...}+$$C_{15}^1\left(3x\right){\left(-4\right)}^{14}+C_{15}^{15}{\left(-4\right)}^{15}$

$=a_{15}{x}^{15}+a_{14}{x}^{14}+\mathrm{...}$$+a_k{x}^k+\mathrm{...}+a_{1}x+a_0$ (với a_i là hệ số của xⁱ).

Thay x = 1, ta được:

(3 . 1 – 4)¹⁵ $=a_{15}{1}^{15}+a_{14}{1}^{14}+\mathrm{...}+$$a_k{1}^k+\mathrm{...}+a_{1}1+a_0$$=a_{15}+a_{14}+\mathrm{...}+a_k+\mathrm{...}+a_1+a_0$

$\Rightarrow a_{15}+a_{14}+\mathrm{...}+a_k+\mathrm{...}+$$a_1+a_0={\left(-1\right)}^{15}=-1.$

Vậy tổng các hệ số của đa thức nhận được là –1.

Bài 10 trang 40 Chuyên đề Toán 10:

Chứng minh rằng các đẳng thức sau đúng với mọi $n\in {\mathbb{N}}^{*}$:

a) $1+2C_n^1+4C_n^2+\dots$$+2^{n-1}{C}_n^{n-1}+2^n{C}_n^n=3^n;$

b) $C_{2n}^0+C_{2n}^2+C_{2n}^4+\dots +C_{2n}^{2n}=$$C_{2n}^1+C_{2n}^3+C_{2n}^5+\dots +C_{2n}^{2n-1}.$

Lời giải:

a)

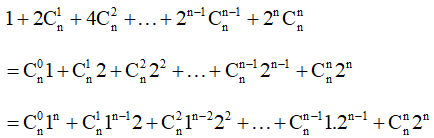
= (1 + 2)ⁿ = 3ⁿ.

b) Ta có:

${(x+1)}^{2n}=C_{2n}^0{x}^{2n}+C_{2n}^1{x}^{2n-1}1$$+C_{2n}^2{x}^{2n-2}{1}^2+\dots +$$C_{2n}^{2n-1}x{1}^{2n-1}+C_{2n}^{2n}{1}^{2n}$

$=C_{2n}^0{x}^{2n}+C_{2n}^1{x}^{2n-1}+$$C_{2n}^2{x}^{2n-2}+\dots +C_{2n}^{2n-1}x+C_{2n}^{2n}.$

Cho x = –1, ta được:

${(-1+1)}^{2n}={\text{C}}_{2n}^0{\left(-1\right)}^{2n}{\text{+C}}_{2n}^1{\left(-1\right)}^{2n-1}$$+{\text{C}}_{2n}^2{\left(-1\right)}^{2n-2}+\dots +{\text{C}}_{2n}^{2n-1}\left(-1\right)+{\text{C}}_{2n}^{2n}$

$={\text{C}}_{2n}^0-{\text{C}}_{2n}^1+{\text{C}}_{2n}^2-\dots -{\text{C}}_{2n}^{2n-1}+{\text{C}}_{2n}^{2n}$

$\Rightarrow {\text{C}}_{2n}^0-{\text{C}}_{2n}^1+{\text{C}}_{2n}^2-\dots$$-{\text{C}}_{2n}^{2n-1}+{\text{C}}_{2n}^{2n}=0$

$\Rightarrow C_{2n}^0+C_{2n}^2+C_{2n}^4+\dots +C_{2n}^{2n}=$$C_{2n}^1+C_{2n}^3+C_{2n}^5+\dots +C_{2n}^{2n-1}.$

Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Elip

Bài 2: Hypebol

Bài 3: Parabol

Bài 4: Tính chất chung của ba đường conic

Bài tập cuối chuyên đề 3