Chuyên đề Toán 10 Bài 2 (Chân trời sáng tạo): Ứng dụng hệ phương trình bậc nhất ba ẩn

Giải bài tập Chuyên đề Toán 10 Bài 2: Ứng dụng hệ phương trình bậc nhất ba ẩn

Giải bài tập trang 14, 17 Chuyên đề Toán 10 Bài 2

Thực hành 1 trang 14 Chuyên đề Toán 10:

Ba vận động viên Hùng, Dũng và Mạnh tham gia thi đấu nội dung ba môn phối hợp: chạy, bơi và đạp xe, trong đó tốc độ trung bình của họ trên mỗi chặng đua được cho ở bảng dưới đây.

Biết tổng thời gian thi đấu ba môn phối hợp của Hùng là 1 giờ 1 phút 30 giây, của Dũng là 1 giờ 3 phút 40 giây và của Mạnh là 1 giờ 1 phút 55 giây. Tính cự li của mỗi chặng đua.

Lời giải:

Đổi: 1 giờ 1 phút 30 giây = $\frac{41}{40}h,$ 1 giờ 3 phút 40 giây = $\frac{191}{180}h,$ 1 giờ 1 phút 55 giây = $\frac{743}{720}h.$

Gọi cự li của mỗi chặng đua chạy, bơi và đạp xe lần lượt là x, y, z (km).

Dựa vào bảng trên ta có hệ phương trình: $\left\{\begin{array}{l}\frac{x}{12,5}+\frac{y}{3,6}+\frac{z}{48}=\frac{41}{40}\\ \frac{x}{12}+\frac{y}{3,75}+\frac{z}{45}=\frac{191}{180}\\ \frac{x}{12.5}+\frac{y}{4}+\frac{z}{45}=\frac{743}{720}\end{array}\right..$

Giải hệ này ta được x = 5, y = 0,75, z = 20.

Vậy ự li của mỗi chặng đua chạy, bơi và đạp xe lần lượt là 5 km; 0,75 km; 20 km.

Thực hành 2 trang 17 Chuyên đề Toán 10:

Một nhà hoá học có ba dung dịch cùng một loại acid nhưng với nồng độ khác nhau là 10%, 20% và 40%. Trong một thí nghiệm, đề tạo ra 100 ml dung dịch nồng độ 18%, nhà hoá học đã sử dụng lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40%. Tính số mililít dung dịch mỗi loại mà nhà hoá học đó đã sử dụng trong thí nghiệm này.

Lời giải:

Gọi lượng dung dịch mỗi loại acid 10%, 20% và 40% mà nhà hoá học sử dụng lần lượt là x, y, z (mililít).

Theo đề bài ta có: x + y + z = 100 (1).

– Dung dịch mới có nồng độ 18%, suy ra $\frac{10\%x+20\%y+40\%z}{100}=18\%$

$$\begin{gathered} \Rightarrow 10\%x+20\%y+40\%z=100.18\% \\ \Rightarrow x+2y+4z=180 \end{gathered}$$ (2).

– Lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40%, suy ra x = 4z hay x – 4z = 0 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=100\\ x+2y+4z=180\\ x-4z=0\end{array}\right..$

Giải hệ này ta được x = 40, y = 50, z = 10.

Vậy lượng dung dịch mỗi loại acid 10%, 20% và 40% mà nhà hoá học sử dụng lần lượt là 40 ml, 50 ml và 10 ml.

Vận dụng 1 trang 17 Chuyên đề Toán 10:

Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,7 và tổng số tế bào con tạo ra là 480. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra. Tính số tế bào con mỗi loại lúc ban đầu.

Lời giải:

Gọi số tế bào con mỗi loại A, B, C lúc ban đầu lần lượt là x, y, z.

Theo đề bài ta có:

– Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,7; suy ra số tế bào con mỗi loại A, B, C được tạo ra lần lượt là 2³x, 2⁴y và 2⁷z hay 8x, 16y và 128z.

– Tổng số tế bào con tạo ra là 480, suy ra 8x + 16y + 128z = 480 (1).

– Khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C, suy ra y = x + z hay x – y + z = 0 (2).

– Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra, suy ra 8x + 128z = 2 . 16y hay 8x – 32y + 128z = 0 hay x – 4y + 16z = 0 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}8x+16y+127z=480\\ x-y+z=0\\ x-4y+16z=0\end{array}\right..$

Giải hệ này ta được x = 8, y = 10, z = 2.

Vậy số tế bào con mỗi loại A, B, C lúc ban đầu lần lượt là 8, 10 và 2.

Vận dụng 2 trang 17 Chuyên đề Toán 10:

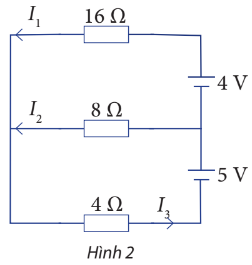
Cho sơ đồ mạch điện như Hình 2.

Tính các cường độ dòng điện I₁, I₂ và I₃.

Lời giải:

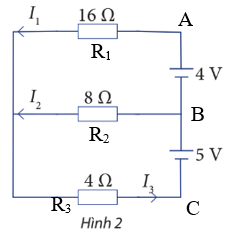
Tổng cường độ dòng điện ra vào vào tại điểm B bằng nhau nên ta có I₁ + I₂ = I₃ (1).

Hiệu điện thế giữa hai điểm A và B được tính bởi:

U_AB = I₁R₁ = I₂R₂, suy ra 16I₁ = 8I₂ (2).

Hiệu điện thế giữa hai điểm A và C được tính bởi:

U_AC = I₁R₁ + I₃R₃ = 16I₁ + 4I₃, suy ra 16I₁ + 4I₃ = 4 + 5 = 9 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}{I}_1+I_2-I_3=0\\ 2I_1-I_2=0\\ 16I_1+4I_3=9\end{array}\right..$

Giải hệ này ta được $I_1=\frac{9}{28},I_2=\frac{9}{14},I_3=\frac{27}{28}.$

Giải bài tập trang 20 Chuyên đề Toán 10 Bài 2

Thực hành 3 trang 20 Chuyên đề Toán 10:

Xét thị trường chè, cà phê và ca cao. Gọi x, y và z lần lượt là giá của 1 kg chè, 1 kg cà phê và 1 kg ca cao (đơn vị: nghìn đồng, x ≥ 0, y ≥ 0, z ≥ 0 ). Các lượng cung và lượng cầu của mỗi sản phẩm được cho như bảng sau:

Tìm giá của mỗi kilôgam chè, cà phê và ca cao để thị trường cân bằng.

Lời giải:

Thị trường cân bằng khi $\left\{\begin{array}{l}{Q}_{S_1}=Q_{D_1}\\ Q_{S_2}=Q_{D_2}\\ Q_{S_3}=Q_{D_3}\end{array}\right.$

$$\begin{gathered} \iff \left\{\begin{array}{l}-380+x+y=350-x-z\\ -405+x+2y-z=760-2y-z\\ -350-2x+3z=145-x+y-z\end{array}\right. \\ \iff \left\{\begin{array}{l}2x+y+z=730\\ x+4y=1165\\ x+y-4z=-495\end{array}\right. \\ \iff \left\{\begin{array}{l}x=125\\ y=260\\ z=220\end{array}\right.. \end{gathered}$$

Vậy để thị trường cân bằng thì giá của mỗi kilôgam chè, cà phê và ca cao lần lợt là 125 nghìn đồng, 260 nghìn đồng và 220 nghìn đồng.

Thực hành 4 trang 20 Chuyên đề Toán 10:

Để mở rộng sản suất, một công ty đã vay 800 triệu đồng từ ba ngân hàng A, B và C, với lãi suất cho vay theo năm lần lượt là 6%, 8% và 9%. Biết rằng tổng số tiền lãi năm đầu tiên công ty phải trả cho ba ngân hàng là 60 triệu đồng và số tiền lãi công ty trả cho hai ngân hàng A và C là bằng nhau. Tính số tiền công ty đã vay từ mỗi ngân hàng.

Lời giải:

Gọi số tiền công ty đã vay từ ba ngân hàng A, B, C lần lượt là x, y, z (triệu đồng).

Theo đề bài ta có:

– Công ty đã vay 800 triệu đồng, suy ra x + y + z = 800 (1).

– Tổng số tiền lãi năm đầu tiên công ty phải trả cho ba ngân hàng là 60 triệu đồng, suy ra 6%x + 8%y + 9%z = 60 hay 6x + 8y + 9z = 6000 (2).

– Số tiền lãi công ty trả cho hai ngân hàng A và C là bằng nhau, suy ra 6%x = 9%z hay 2x – 3z = 0 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=800\\ 6x+8y+9z=6000\\ 2x-3z=0\end{array}\right..$

Giải hệ này ta được x = 300, y = 300, z = 200.

Vậy số tiền công ty đã vay từ ba ngân hàng A, B, C lần lượt là 300 triệu đồng, 300 triệu đồng và 200 triệu đồng.

Thực hành 5 trang 20 Chuyên đề Toán 10:

Bác Nhân có 650 triệu đồng dự định gửi tiết kiệm vào các ngân hàng A, B và C. Biết các ngân hàng A, B, C trả lãi suất lần lượt là 8%/năm, 7,5%/năm và 7%/năm. Để phù hợp với nhu cầu, bác Nhân mong muốn sau một năm, tổng số tiền lãi bác nhận được là 50 triệu đồng và số tiền bác gửi vào ngân hàng B lớn hơn số tiền gửi vào ngân hàng C là 100 triệu đồng. Hãy tính giúp bác Nhân số tiền gửi vào mỗi ngân hàng sao cho đáp ứng được yêu cầu của bác.

Lời giải:

Gọi số tiền bác Nhân gửi vào mỗi ngân hàng A, B, C lần lượt là x, y, z (triệu đồng).

Theo đề bài ta có:

– Tổng số tiền bác có là 650 triệu đồng, suy ra x + y + z = 650 (1).

– Tổng số tiền lãi bác nhận được sau một năm là 50 triệu đồng, suy ra 8%x + 7,5%y + 7%z = 50 hay 8x + 7,5y + 7z = 5000 (2).

– Số tiền bác gửi vào ngân hàng B lớn hơn số tiền gửi vào ngân hàng C là 100 triệu đồng, suy ra y – z = 100 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=650\\ 8x+7,5y+7z=5000\\ y-z=100\end{array}\right..$

Giải hệ này ta được x = 350, y = 200, z = 100.

Vậy số tiền bác Nhân gửi vào mỗi ngân hàng A, B, C lần lượt là 350 triệu đồng, 200 triệu đồng và 100 triệu đồng.

Vận dụng 3 trang 20 Chuyên đề Toán 10:

Một công ty sản xuất ba loại phân bón:

 –  Loại A có chứa 18% nitơ, 4% photphat và 5% kali;

 –  Loại B có chứa 20% nitơ, 4% photphat và 4% kali;

 –  Loại C có chứa 24% nitơ, 3% photphat và 6% kali.

Công ty sản xuất bao nhiêu kilôgam mỗi loại phân bón trên? Biết rằng công ty đã dùng hết 26400 kg nitơ, 4900 kg photphat, 6200 kg kali.

Lời giải:

Gọi khối lượng mỗi loại phân bón A, B, C lần lượt là x, y, z (kilôgam).

Theo đề bài ta có:

– Công ty dùng hết 26400 kg nitơ, suy ra 18%x + 20%y + 24%z = 26400 hay 18x + 20y + 24z = 2640000 (1).

– Công ty dùng hết 4900 kg photphat, suy ra 4%x + 4%y + 3%z = 4900 hay 4x + 4y + 3z = 490000 (2).

– Công ty dùng hết 6200 kg kali, suy ra 5%x + 4%y + 6%z = 4900 hay 5x + 4y + 6z = 620000 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}18x+20y+24z=2640000\\ 4x+4y+3z=490000\\ 5x+4y+6z=620000\end{array}\right..$

Giải hệ này ta được x = 40000, y = 60000, z = 30000.

Vậy khối lượng mỗi loại phân bón A, B, C lần lượt là 40000kg, 60000kg và 30000 kg.

Giải bài tập trang 21 Chuyên đề Toán 10 Bài 2

Bài 1 trang 21 Chuyên đề Toán 10:

Một đại lí bán ba mẫu máy điều hoà A, B và C, với giá bán mỗi chiếc theo từng mẫu lần lượt là 8 triệu đồng, 10 triệu đồng và 12 triệu đồng. Tháng trước, đại lí bán được 100 chiếc gồm cả ba mẫu và thu được số tiền là 980 triệu đồng. Tính số lượng máy điều hoà mỗi mẫu đại lí bán được trong tháng trước, biết rằng số tiền thu được từ bán máy điều hoà mẫu A và mẫu C là bằng nhau.

Lời giải:

Gọi số lượng máy điều hoà mỗi mẫu A, B, C đại lí bán được trong tháng trước lần lượt là x, y, z.

Theo đề bài ta có:

– Đại lí bán được 100 chiếc gồm cả ba mẫu, suy ra x + y + z = 100 (1).

– Số tiền thu được là 980 triệu đồng, suy ra 8x + 10y + 12z = 980 hay 4x + 5y + 6z = 490 (2).

– Số tiền thu được từ bán máy điều hoà mẫu A và mẫu C là bằng nhau, suy ra 8x = 12z hay 2x –3z = 0 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=100\\ 4x+5y+6z=490\\ 2x-3z=0\end{array}\right..$

Giải hệ này ta được x = 30, y = 50, z = 20.

Vậy số lượng máy điều hoà mỗi mẫu A, B, C đại lí bán được trong tháng trước lần lượt là 30, 50, 20.

Bài 2 trang 21 Chuyên đề Toán 10:

Nhân dịp kỉ niệm ngày thành lập Đoàn Thanh niên Cộng sản Hồ Chí Minh, một trường Trung học phổ thông đã tổ chức cho học sinh tham gia các trò chơi. Ban tổ chức đã chọn 100 bạn và chia thành ba nhóm A, B, C để tham gia trò chơi thứ nhất. Sau khi trò chơi kết thúc, ban tổ chức chuyển $\frac{1}{3}$ số bạn ở nhóm A sang nhóm B; $\frac{1}{2}$ số bạn ở nhóm B sang nhóm C; số bạn chuyển từ nhóm C sang nhóm A và B đều bằng $\frac{1}{3}$ số bạn ở nhóm C ban đầu. Tuy nhiên, người ta nhận thấy số bạn ở mỗi nhóm là không đổi qua hai trò chơi. Ban tổ chức đã chia mỗi nhóm bao nhiêu bạn?

Lời giải:

Gọi số bạn trong mỗi nhóm A, B, C lần lượt là x, y, z.

Theo đề bài ta có: x + y + z = 100 (1).

– Số bạn ở nhóm A sau khi chuyển là: x – $\frac{1}{3}x+\frac{1}{3}z;$

– Số bạn ở nhóm B sau khi chuyển là: y – $\frac{1}{2}y+\frac{1}{3}x+\frac{1}{3}z;$

Vì số bạn ở mỗi nhóm là không đổi qua hai trò chơi nên ta có:

$$\begin{gathered} \left\{\begin{array}{l}x-\frac{1}{3}x+\frac{1}{3}z=x\\ y-\frac{1}{2}y+\frac{1}{3}x+\frac{1}{3}z=y\end{array}\right. \\ \Rightarrow \left\{\begin{array}{l}x-z=0\left(2\right)\\ 2x-3y+2z=0\left(3\right)\end{array}\right.. \end{gathered}$$

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=100\\ x-z=0\\ 2x-3y+2z=0\end{array}\right..$

Giải hệ này ta được x = 30, y = 40, z = 30.

Vậy số bạn trong mỗi nhóm A, B, C lần lượt là 30, 40, 30.

Bài 3 trang 21 Chuyên đề Toán 10:

Một cửa hàng giải khát chỉ phục vụ ba loại sinh tố: xoài, bơ và mãng cầu. Để pha mỗi li (cốc) sinh tố này đều cần dùng đến sữa đặc, sữa tươi và sữa chua với công thức cho ở bảng sau.

 Ngày hôm qua cửa hàng đã dùng hết 2 l sữa đặc; 12,8 l sữa tươi và 2,9 l sữa chua. Cửa hàng đã bán được bao nhiêu li sinh tố mỗi loại trong ngày hôm qua?

Lời giải:

Gọi số li sinh tố mỗi loại xoài, bơ, mãng cầu cửa hàng bán được trong ngày hôm qua lần lượt là x, y, z.

Theo đề bài ta có:

– Cửa hàng đã dùng hết 2 l hay 2000 ml sữa đặc, suy ra 20x + 10y + 20z = 2000 hay 2x + y + 2z = 200 (1).

– Cửa hàng đã dùng hết 12,8 l hay 12800 ml sữa tươi, suy ra 100x + 120y + 100z = 12800 hay 5x + 6y + 5z = 640 (2).

– Cửa hàng đã dùng hết 2,9 l hay 2900 ml sữa chua, suy ra 30x + 20y + 20z = 2900 hay 3x + 2y + 2z = 290 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}2x+y+2z=200\\ 5x+6y+5z=640\\ 3x+2y+2z=290\end{array}\right..$

Giải hệ này ta được x = 50, y = 40, z = 30.

Vậy số li sinh tố mỗi loại xoài, bơ, mãng cầu cửa hàng bán được trong ngày hôm qua lần lượt là 50, 40, 30.

Bài 4 trang 21 Chuyên đề Toán 10:

Ba tế bào A, B, C sau một số lần nguyên phân tạo ra 168 tế bào con. Biết số tế bào A tạo ra gấp bốn lần số tế bào B tạo ra và số lần nguyên phân của tế bào C nhiều hơn số lần nguyên phân của tế bào B là bốn lần. Tính số lần nguyên phân của mỗi tế bào.

Lời giải:

Gọi số lần nguyên phân của mỗi tế bào A, B, C lần lượt là x, y, z.

Theo đề bài ta có:

– Sau nguyên phân tạo ra 168 tế bào con, suy ra 2^x + 2^y + 2^z = 168 (1).

– Số tế bào A tạo ra gấp bốn lần số tế bào B tạo ra, suy ra 2^x = 4 . 2^y hay 2^x – 4 . 2^y = 0 (2).

– Số lần nguyên phân của tế bào C nhiều hơn số lần nguyên phân của tế bào B là bốn lần, suy ra y + 4 = z, suy ra 2^{y + 4} = 2^z hay 16 . 2^y – 2^z = 0 (3).

Đặt a = 2^x, b = 2^y, c = 2^z thì từ (1), (2) và (3) ta có hệ phương trình:

$\left\{\begin{array}{l}a+b+c=168\\ a-4b=0\\ 16b-c=0\end{array}\right..$

Giải hệ này ta được a = 32, b = 8, c = 128.

Suy ra x = 5, y = 3, z = 7.

Vậy số lần nguyên phân của mỗi tế bào A, B, C lần lượt là 5, 3, 7.

Bài 5 trang 21 Chuyên đề Toán 10:

Cho sơ đồ mạch điện như Hình 3. Biết R₁ = 4 Ω, R₂ = 4 Ω và R₃ = 8 Ω. Tìm các cường độ dòng điện I₁, I₂ và I₃.

Lời giải:

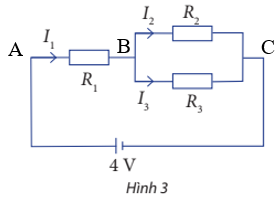
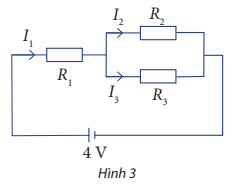
Tổng cường độ dòng điện ra vào vào tại điểm B bằng nhau nên ta có I₁ = I₂ + I₃ (1).

Hiệu điện thế giữa hai điểm A và C được tính bởi:

U_AC = I₁R₁ + I₃R₃ = 4I₁ + 8I₃, suy ra 4I₁ + 8I₃ = 6 hay 2I₁ + 4I₃ = 3 (2).

Hiệu điện thế giữa hai điểm B và C được tính bởi:

U_BC = I₂R₂ = I₃R₃, suy ra 4I₂ = 8I₃ hay I₂ = 2I₃ (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}{I}_1-I_2-I_3=0\\ 2I_1+4I_3=3\\ I_2-2I_3=0\end{array}\right..$

Giải hệ này ta được $I_1=\frac{9}{10},I_2=\frac{3}{5},I_3=\frac{3}{10}.$

Giải bài tập trang 22, 23 Chuyên đề Toán 10 Bài 2

Bài 6 trang 22 Chuyên đề Toán 10:

Cân bằng phương trình phản ứng khi đốt cháy khí methane trong oxygen:

CH₄ + O₂ $\stackrel{t^o}{\to }$ CO₂ + H₂O.

Lời giải:

Gọi x, y, z, t lần lượt là bốn số nguyên dương thoả mãn cân bằng phương trình phản ứng hoá học:

xCH₄ + yO₂ $\stackrel{t^o}{\to }$ zCO₂ + tH₂O.

Số nguyên tử C ở hai vế bằng nhau, ta có x = z (1).

Số nguyên từ H ở hai vế bằng nhau, ta có 4x = 2t hay 2x = t (2).

Số nguyên từ O ở hai vế bằng nhau, ta có 2y = 2z + t (3).

Thay (1) và (2) vào (3) ta được 2y = 2x + 2x hay y = 2x.

Vậy y = 2x, z = x, t = 2x.

Để phương trình có hệ số đơn giản, ta chọn x = 1, khi đó y = 2, z = 1, t = 2.

Vậy phương trình cân bằng phản ứng hoá học là CH₄ + 2O₂ $\stackrel{t^o}{\to }$ CO₂ + 2H₂O.

Bài 7 trang 22 Chuyên đề Toán 10:

Một nhà máy có ba bộ phận cắt, may, đóng gói để sản xuất ba loại sản phẩm: áo thun, áo sơ mi, áo khoác. Thời gian (tính bằng phút) của mỗi bộ phận để sản xuất 10 cái áo mỗi loại được thể hiện trong bảng sau:

Các bộ phận cắt, may và đóng gói có tối đa 80, 160 và 48 giờ lao động tương ứng mỗi ngày. Hãy lập kế hoạch sản xuất để nhà máy hoạt động hết công suất.

Lời giải:

Đổi: 80 giờ = 4800 phút, 160 giờ = 9600 phút, 48 giờ = 2880 phút.

Nhà máy hoạt động hết công suất nghĩa là sử dụng được hết thời gian lao động tối đa.

Gọi số lượng áo thun, áo sơ mi, áo khoác cần sản xuất để nhà máy hoạt động hết công suất lần lượt là x, y, z (x, y, z nguyên dương).

Dựa vào bảng trên ta có hệ phương trình: $\left\{\begin{array}{l}9x+12y+15z=4800\\ 22x+24y+28z=9600\\ 6x+8y+8z=2880\end{array}\right..$

Giải hệ này ta được x = 80, y = 140, z = 160.

Vậy số lượng áo thun, áo sơ mi, áo khoác cần sản xuất để nhà máy hoạt động hết công suất lần lượt là 80, 140, 160.

Bài 8 trang 22 Chuyên đề Toán 10:

Bà Hà có 1 tỉ đồng để đầu tư vào cổ phiếu, trái phiếu và gửi tiết kiệm ngân hàng. Cổ phiếu sinh lợi nhuận 12%/năm, trong khi trái phiếu và gửi tiết kiệm ngân hàng cho lãi suất lần lượt là 8%/năm và 4%/năm. Bà Hà đã quy định rằng số tiền gửi tiết kiệm ngân hàng phải bằng tổng của 20% số tiền đầu tư vào cổ phiếu và 10% số tiền đầu tư vào trái phiếu. Bà Hà nên phân bổ nguồn vốn của mình như thế nào để nhận được 100 triệu đồng tiền lãi từ các khoản đầu tư đó trong năm đầu tiên?

Lời giải:

Gọi số tiền bác Hà nên đầu tư vào cổ phiếu, trái phiếu và gửi tiết kiệm ngân hàng lần lượt là x, y, z (triệu đồng).

Theo đề bài ta có:

– Bác Hà có 1 tỉ đồng, suy ra x + y + z = 1000 (1).

– Số tiền gửi tiết kiệm ngân hàng bằng tổng của 20% số tiền đầu tư vào cổ phiếu và 10% số tiền đầu tư vào trái phiếu, suy ra z = 20%x + 10%y hay 2x + y – 10z = 0 (2).

– Số tiền lãi là 100 triệu đồng, suy ra 12%x + 8%y + 4%z = 100 hay 3x + 2y + z = 2500 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=1000\\ 2x+y-10z=0\\ 3x+2y+z=2500\end{array}\right..$

Giải hệ này ta được x = 650, y = 200, z = 150.

Vậy số tiền bác Hà nên đầu tư vào cổ phiếu, trái phiếu và gửi tiết kiệm ngân hàng lần lượt là 650 triệu đồng, 200 triệu đồng, 150 triệu đồng.

Bài 9 trang 22 Chuyên đề Toán 10:

Trên thị trường có ba loại sản phẩm A, B, C với giá mỗi tấn sản phẩm tương ứng là x, y, z (đơn vị: triệu đồng, x ≥ 0, y ≥ 0, z ≥ 0). Lượng cung và lượng cầu của mỗi sản phẩm được cho trong bảng dưới đây:

Tìm giá bán của mỗi sản phẩm để thị trường cân bằng.

Lời giải:

Thị trường cân bằng khi $\left\{\begin{array}{l}{Q}_{S_A}=Q_{D_A}\\ Q_{S_B}=Q_{D_B}\\ Q_{S_C}=Q_{D_C}\end{array}\right.$

$$\begin{gathered} \iff \left\{\begin{array}{l}4x-y-z-5=-2x+y+z+9\\ -x+4y-z-5=x-2y+z+3\\ -x-y+4z-1=x+y-2z-1\end{array}\right. \\ \iff \left\{\begin{array}{l}6x-2y-2z=14\\ 2x-6y+2z=-8\\ 2x+2y-6z=0\end{array}\right. \end{gathered}$$

$$\begin{gathered} \iff \left\{\begin{array}{l}3x-y-z=7\\ x-3y+z=-4\\ x+y-3z=0\end{array}\right. \\ \iff \left\{\begin{array}{l}x=4,5\\ y=3,75\\ z=2,75\end{array}\right.. \end{gathered}$$

Vậy giá mỗi mỗi sản phẩm A, B, C để thị trường cân bằng lần lượt là 4,5 triệu đồng; 3,75 triệu đồng; 2,75 triệu đồng.

Bài 10 trang 23 Chuyên đề Toán 10:

Vé vào xem một vở kịch có ba mức giá khác nhau tuỳ theo khu vực ngồi trong nhà hát. Số lượng vé bán ra và doanh thu của ba suất diễn được cho bởi bảng sau:

 Tìm giá vé ứng với mỗi khu vực ngồi trong nhà hát.

Lời giải:

Gọi giá vé ứng với mỗi khu vực 1, khu vực 2, khu vực 3 lần lượt là x, y, z (triệu đồng).

Dựa vào bảng trên ta có hệ phương trình: $\left\{\begin{array}{l}210x+152y+125z=212,7\\ 225x+165y+118z=224,4\\ 254x+186y+130z=252,2\end{array}\right..$

Giải hệ này ta được x = 0,4; y = 0,6; z = 0,3.

Vậy giá vé ứng với mỗi khu vực 1, khu vực 2, khu vực 3 lần lượt là 400 nghìn đồng, 600 nghìn đồng và 300 nghìn đồng.

Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chuyên đề 1

Bài 1: Phương pháp quy nạp toán học

Bài 2: Nhị thức Newton

Bài tập cuối chuyên đề 2

Bài 1: Elip