Nội dung bài viết

    Xem thêm

    Chứng minh rằng các đẳng thức sau đúng với mọi n thuộc N*: 1^3+2^3+3^3+...+n^3=[n^2(n+1)^2]/4

    Lời giải Bài 1 trang 40 sách Chuyên đề Toán lớp 10 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập.

    1 410 08/11/2022
    Trang trước
    Trang sau  

    Giải Chuyên đề Toán 10 Chân trời sáng tạo Bài tập cuối chuyên đề 2

    Bài 1 trang 40 Chuyên đề Toán 10:

    Chứng minh rằng các đẳng thức sau đúng với mọi n∈ℕ*.

    a) 13+23+33+…+n3=n2(n+1)24;

    b) 1.4+2.7+3.10+…+n(3n+1)=n(n+1)2;

    c) 11.3+13.5+15.7+…+1(2n−1)(2n+1)=n2n+1.

    Lời giải:

    a) Bước 1. Với n = 1, ta có 13 = 12(1+1)24. Do đó đẳng thức đúng với n = 1.

    Bước 2. Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

    13+23+33+…+k3=k2(k+1)24.

    Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

    13+23+33+…+k3+(k+1)3=(k+1)2[(k+1)+1]24.

    Sử dụng giả thiết quy nạp, ta có:

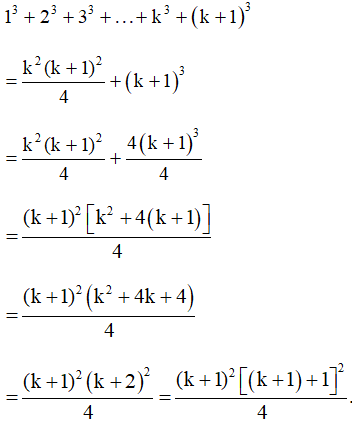
    Chuyên đề Toán 10 Bài tập cuối chuyên đề 2 - Chân trời sáng tạo (ảnh 1)

    Vậy đẳng thức đúng với n = k + 1.

    Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

    b) Bước 1. Với n = 1, ta có 1(3 . 1 + 1) = 4 = 1(1 +  1)2. Do đó đẳng thức đúng với n = 1.

    Bước 2. Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

    1.4+2.7+3.10+…+k(3k+1)=k(k+1)2.

    Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

    1.4+2.7+3.10+…+k(3k+1)+(k+1)[3(k+1)+1]=(k+1)[(k+1)+1]2.

    Sử dụng giả thiết quy nạp, ta có:

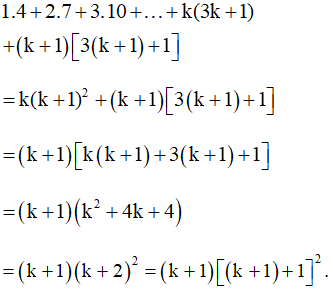
    Chuyên đề Toán 10 Bài tập cuối chuyên đề 2 - Chân trời sáng tạo (ảnh 1)

    Vậy đẳng thức đúng với n = k + 1.

    Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

    c) Bước 1. Với n = 1, ta có 1(2.1−1)(2.1+1)=13=12.1+1. Do đó đẳng thức đúng với n = 1.

    Bước 2. Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

    11.3+13.5+15.7+…+1(2k−1)(2k+1)=k2k+1.

    Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

    11.3+13.5+15.7+…+1(2k−1)(2k+1)+1[2(k+1)−1][2(k+1)+1]=k+12(k+1)+1.

    Sử dụng giả thiết quy nạp, ta có:

    11.3+13.5+15.7+…+1(2k−1)(2k+1)+1[2(k+1)−1][2(k+1)+1]

    =k2k+1+1[2(k+1)−1][2(k+1)+1]

    =k2k+1+1(2k+1)(2k+3)

    =k(2k+3)+1(2k+1)(2k+3)

    =2k2+3k+1(2k+1)(2k+3)

    =(k+1)(2k+1)(2k+1)(2k+3)=k+12k+3=k+12(k+1)+1.

    Vậy đẳng thức đúng với n = k + 1.

    Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài 2 trang 40 Chuyên đề Toán 10: Chứng minh rằng với mọi n ∈ℕ*: a) 3n – 1 – 2n chia hết cho 4...

    Bài 3 trang 40 Chuyên đề Toán 10: Chứng minh rằng 8n ≥ n3 với mọi n ∈ℕ*...

    Bài 4 trang 40 Chuyên đề Toán 10: Chứng minh rằng bất đẳng thức 1+12+13+…+1n≤n+12...

    Bài 5 trang 40 Chuyên đề Toán 10: Với một bình rỗng có dung tích 2 l, một bạn học sinh thực hiện thí nghiệm theo các bước...

    Bài 6 trang 40 Chuyên đề Toán 10: Tìm hệ số của x3 trong khai triển: a) (1 – 3x)8...

    Bài 7 trang 40 Chuyên đề Toán 10: Tìm hệ số của x5 trong khai triển (2x + 3)(x – 2)6...

    Bài 8 trang 40 Chuyên đề Toán 10: a) Tìm ba số hạng đầu tiên trong khai triển của (1 + 2x)6, các số hạng được viết theo thứ tự số mũ...

    Bài 9 trang 40 Chuyên đề Toán 10: Trong khai triển biểu thức (3x – 4)15 thành đa thức, hãy tính tổng các hệ số...

    Bài 10 trang 40 Chuyên đề Toán 10: Chứng minh rằng các đẳng thức sau đúng với mọi n∈ℕ*: Bài 10 trang 40 Chuyên đề Toán 10...

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài 1: Elip

    Bài 2: Hypebol

    Bài 3: Parabol

    Bài 4: Tính chất chung của ba đường conic

    Bài tập cuối chuyên đề 3

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 410 08/11/2022
    Trang trước
    Trang sau  

    Xem thêm các chương trình khác: