Chứng minh rằng nếu phép dời hình F biến tam giác ABC thành tam giác A'B'C' thì F

Lời giải Bài 15 trang 25 Chuyên đề Toán 11 sách Chuyên đề học tập Toán lớp 11 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập.

1 427 03/07/2023

Trang trước

Trang sau

Giải Chuyên đề Toán 11 Cánh diều Bài 1: Phép dời hình

Bài 15 trang 25 Chuyên đề Toán 11: Chứng minh rằng nếu phép dời hình F biến tam giác ABC thành tam giác A'B'C' thì F lần lượt biến trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC thành trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác A'B'C'.

Lời giải:

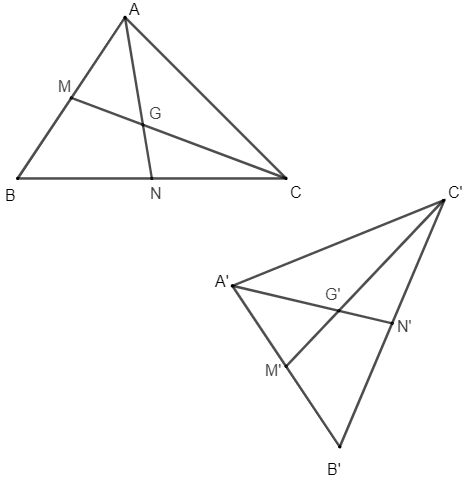
Bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều

+) Phép dời hình F biến tam giác ABC thành tam giác A'B'C', do đó F biến các đoạn thẳng AB, BC tương ứng thành các đoạn thẳng A'B', B'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, BC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', B'C'. Vậy F biến các trung tuyến CM, AN của tam giác ABC tương ứng thành các trung tuyến C'M', A'N' của tam giác A'B'C'. Từ đó suy ra F biến trọng tâm G của tam giác ABC là giao của CM và AN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và A'N'.

+) Gọi AH là đường cao của tam giác ABC (H ∈ BC). Khi đó phép dời hình F biến đường thẳng AH thành đường thẳng A'H'. Vì AH ⊥ BC nên A'H' ⊥ B'C', nói cách khác A'H' là đường cao của tam giác A'B'C'. Đối với các đường cao khác cũng thế. Vì trực tâm tam giác là giao điểm của các đường cao nên trực tâm tam giác ABC biến thành trực tâm tam giác A'B'C'.

+) Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC thì OA = OB = OC nên nếu điểm O biến thành điểm O' qua phép dời hình F thì O'A' = O'B' = O'C' = OA = OB = OC, do đó O' là tâm đường tròn ngoại tiếp tam giác A'B'C'.

Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Cánh diều hay, chi tiết khác:

Khởi động trang 5 Chuyên đề Toán 11: Thang băng chuyền tải khách (Hình 1) là loại thang máy không có bậc thang...

Hoạt động 1 trang 5 Chuyên đề Toán 11: Trong mặt phẳng cho đường thẳng d và điểm M....

Hoạt động 2 trang 6 Chuyên đề Toán 11: Cho vectơ u và điểm M trong mặt phẳng. Hãy xác định điểm M'

Luyện tập 1 trang 7 Chuyên đề Toán 11: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo...

Hoạt động 3 trang 7 Chuyên đề Toán 11: Cho phép tịnh tiến u và hai điểm M, N. Giả sử...

Hoạt động 4 trang 7 Chuyên đề Toán 11: Xét phép tịnh tiến theo vectơ (Hình 5).

Luyện tập 2 trang 9 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm O(0; 0)...

Hoạt động 5 trang 10 Chuyên đề Toán lớp 11: Trong mặt phẳng cho đường thẳng d. Với mỗi điểm M....

Luyện tập 3 trang 10 Chuyên đề Toán 11: Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm...

Hoạt động 6 trang 11 Chuyên đề Toán lớp 11: Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x₁; y₁), N(x₂; y₂)....

Hoạt động 7 trang 11 Chuyên đề Toán lớp 11: Xét phép đối xứng trục d (Hình 11)