Cho tam giác ABC. Khẳng định nào sau đây là đúng?

Đáp án đúng là: B.

*Lời giải

Áp dụng công thức tính diện tích tam giác ta có:

\(S = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B\)

Suy ra: \(\sin A = \frac{{2S}}{{bc}}\); \(\sin B = \frac{{2S}}{{ac}}\); \(\sin C = \frac{{2S}}{{ab}}\).

Lại có: \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\); \(\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\).

Do đó, ta có:

 sin B. cos C + sin C. cos B  

= \(\frac{{2S}}{{ac}}.\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} + \frac{{2S}}{{ab}}.\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)

\( = \frac{S}{{{a^2}bc}}\left( {{a^2} + {b^2} - {c^2} + {a^2} + {c^2} - {b^2}} \right)\)

\( = \frac{S}{{{a^2}bc}}.2{a^2} = \frac{{2S}}{{bc}} = \sin A\).

Vậy sinA = sin B. cos C + sin C. cos B.

*Phương pháp giải

Áp dụng kiến thức về định lý sin và cosin để tính:

Ta có công thức tính diện tích tam giác ABC là:

$S=\frac{1}{2}bc\sin A=\frac{1}{2}ac\sin B=\frac{1}{2}ab\sin C.$

*Lý thuyết cần nắm thêm về định lý cosin và định lý sin

- Định lí Côsin:

Cho tam giác ABC bất kì với AB = c, AC = b, BC = a.

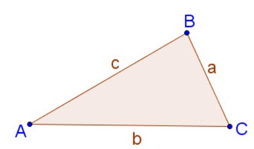
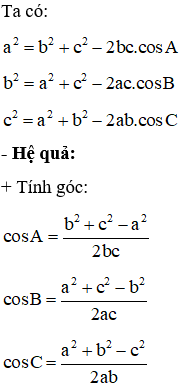
+ Tính diện tích:

$S=\frac{1}{2}BC.h_a=\frac{1}{2}AC.h_b=\frac{1}{2}AB.h_c$. ($h_a,h_b,h_c$ là độ dài đường cao lần lượt kẻ từ đỉnh A, B, C)

$S=\frac{1}{2}ab\sin C=\frac{1}{2}ac\sin B=\frac{1}{2}bc\sin A$

$S=\frac{abc}{4R}$ (với R là bán kính đường tròn ngoại tiếp)

S = pr (với r là bán kính đường tròn nội tiếp, $p=\frac{a+b+c}{2}$)

$S=\sqrt{p(p-a)(p-b)(p-c)}$ (với $p=\frac{a+b+c}{2}$) (công thức Hê – rông)

II. Các công thức cần nhớ.

Cho tam giác ABC bất kì có diện tích S với AB = c, AC = b, BC = a. Ta có:

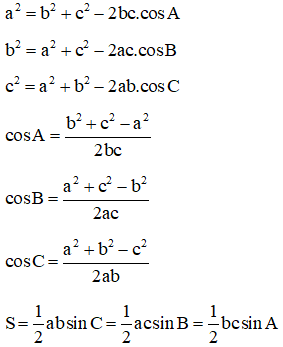
$S=\frac{abc}{4R}$ (với R là bán kính đường tròn ngoại tiếp)

S = pr (với r là bán kính đường tròn nội tiếp, $p=\frac{a+b+c}{2}$)

$S=\sqrt{p(p-a)(p-b)(p-c)}$ (với $p=\frac{a+b+c}{2}$) (công thức Hê – rông)

Định lí sin trong tam giác

Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R;$

Trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.

Từ định lí sin, ta có hệ quả sau đây:

Hệ quả:

a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;

$\sin A=\frac{a}{2R};\sin B=\frac{b}{2R};\sin C=\frac{c}{2R}.$ 

Xem thêm một số bài viết liên quan hay, chi tiết:

Lý thuyết Định lí côsin và định lí sin – Toán 10 Chân trời sáng tạo

TOP 20 câu Trắc nghiệm Định lí côsin và định lí sin (Chân trời sáng tạo 2024) có đáp án - Toán 10