Câu hỏi:
20/07/2024 148
Cho tam giác ABC có I là trung điểm của BC. Điểm M thỏa mãn là
Cho tam giác ABC có I là trung điểm của BC. Điểm M thỏa mãn là
A. M là trung điểm của BC (M và I trùng nhau);
A. M là trung điểm của BC (M và I trùng nhau);
B. M là trọng tâm tam giác ABC;
C. M đối xứng với A qua I;
D. M là điểm sao cho ABMC là hình bình hành.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
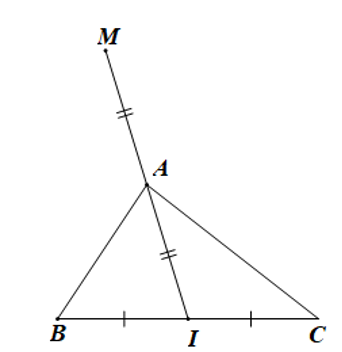
Gọi I là trung điểm của BC.
Suy ra với điểm M bất kì ta có .
Mà nên hay
Do đó ba điểm M, A, I thẳng hàng sao cho 2MA = MI.
Suy ra A là trung điểm của MI hay M đối xứng với A qua I.
Vậy ta chọn phương án C.
Đáp án đúng là: C
Gọi I là trung điểm của BC.
Suy ra với điểm M bất kì ta có .
Mà nên hay
Do đó ba điểm M, A, I thẳng hàng sao cho 2MA = MI.
Suy ra A là trung điểm của MI hay M đối xứng với A qua I.
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC, M là trung điểm của BC, N là điểm thuộc cạnh AC sao cho AN = 2NC. Biểu diễn vectơ theo và ta được
Cho tam giác ABC, M là trung điểm của BC, N là điểm thuộc cạnh AC sao cho AN = 2NC. Biểu diễn vectơ theo và ta được
Câu 3:
Gọi G là trọng tâm tam giác ABC. Gọi . Giá trị của m và n để có là
Gọi G là trọng tâm tam giác ABC. Gọi . Giá trị của m và n để có là
Câu 5:
Cho tam giác ABC có D là trung điểm của BC và G là trọng tâm tam giác ABC.
Đẳng thức nào sau đây đúng?
Cho tam giác ABC có D là trung điểm của BC và G là trọng tâm tam giác ABC.
Đẳng thức nào sau đây đúng?
Câu 6:
Cho tam giác ABC. M là điểm bất kì thỏa mãn . Chọn khẳng định đúng?
Cho tam giác ABC. M là điểm bất kì thỏa mãn . Chọn khẳng định đúng?
Câu 7:
Cho tam giác ABC, M là trung điểm của BC, I là điểm bất kì. Khẳng định nào sau đây đúng?
Cho tam giác ABC, M là trung điểm của BC, I là điểm bất kì. Khẳng định nào sau đây đúng?


