Câu hỏi:
13/11/2024 2,030
Cho hàm số f(x)=cos x+x. Khẳng định nào dưới đây đúng?
Cho hàm số f(x)=cos x+x. Khẳng định nào dưới đây đúng?
A. ∫f(x)dx=−sin x+x2+C.
B. ∫f(x)dx=sin x+x2+C.
C. ∫f(x)dx=−sin x+x22+C.
D. ∫f(x)dx=sin x+x22+C.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Lời giải:
∫f(x)dx=∫[cos x+x]dx=sin x+x22+C.
*Phương pháp giải:
Áp dụng:
- Tính chất 3.
∫[f(x) ± g(x)]dx= ∫f(x) dx ±∫g(x) dx
- Tính nguyên hàm từng cái:
+ nguyên hàm của cosx = sinx
+ nguyên hàm của x = x2/x
*Lý thuyến cần nắm và dạng toán về nguyên hàm:
- Định nghĩa
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng của R).
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x∈K.
- Định lí 1.
Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
- Định lí 2.
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x)+C; C∈ℝ là họ tất cả các nguyên hàm của f(x) trên K. Kí hiệu: ∫f(x)dx=F(x)+C
- Chú ý: Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì dF(x) = F’(x)dx = f(x)dx.
Tính chất của nguyên hàm
- Tính chất 1.
∫f'
- Tính chất 2.
(k là hằng số khác 0).
- Tính chất 3.
Bảng nguyên hàm của một số hàm số thường gặp

Phương pháp tính nguyên hàm.
1. Phương pháp đổi biến số
- Định lí 1.
Nếu và u = u(x) là hàm số có đạo hàm liên tục thì:
Hệ quả: Nếu u = ax + b (a ≠ 0), ta có:
Chú ý:
Nếu tính nguyên hàm theo biến mới u (u = u(x)) thì sau khi tính nguyên hàm, ta phải trở lại biến x ban đầu bằng cách thay u bởi u(x).
2. Phương pháp tính nguyên hàm từng phần.
- Định lí 2.
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
- Chú ý.
Vì u’(x) dx = du; v’(x) dx = dv. Nên đẳng thức trên còn được viết ở dạng:
Đó là công thức nguyên hàm từng phần.
CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
1. Dạng trong đó m, n là các số tự nhiên.
Trường hợp 1: Trong hai số m, n có ít nhất một số lẻ.
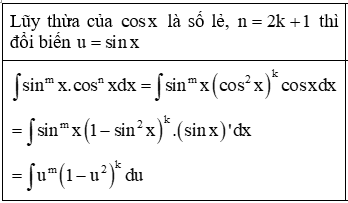
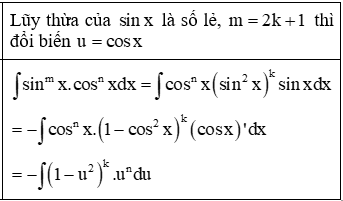
Trường hợp 2: Cả hai số m, n đều là số chẵn: Ta sử dụng công thức hạ bậc để giảm một nửa số mũ của , để làm bài toán trở nên đơn giản hơn.
2. Dạng ;
; ;
.
Ta sử dụng công thức biến đổi tích thành tổng trong lượng giác.
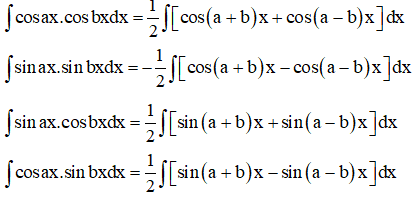
3. Dạng trong đó m, n là các số nguyên.

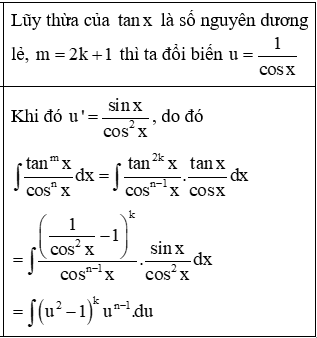
4. Đổi biến số với hàm lượng giác.
Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các dạng , thì ta có cách biến đổi lượng giác như sau:

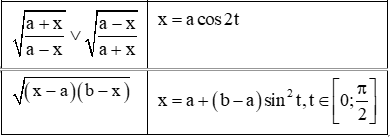
Xem thêm các bài viết liên quan hay, chi tiết
- Tính chất 3.
∫[f(x) ± g(x)]dx= ∫f(x) dx ±∫g(x) dx
- Tính nguyên hàm từng cái:
+ nguyên hàm của cosx = sinx
+ nguyên hàm của x = x2/x
- Định nghĩa
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng của R).
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x∈K.
- Định lí 1.
Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
- Định lí 2.
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x)+C; C∈ℝ là họ tất cả các nguyên hàm của f(x) trên K. Kí hiệu: ∫f(x)dx=F(x)+C
- Chú ý: Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì dF(x) = F’(x)dx = f(x)dx.
Tính chất của nguyên hàm
- Tính chất 1.
∫f'
- Tính chất 2.
(k là hằng số khác 0).
- Tính chất 3.
Bảng nguyên hàm của một số hàm số thường gặp

Phương pháp tính nguyên hàm.
1. Phương pháp đổi biến số
- Định lí 1.
Nếu và u = u(x) là hàm số có đạo hàm liên tục thì:
Hệ quả: Nếu u = ax + b (a ≠ 0), ta có:
Chú ý:
Nếu tính nguyên hàm theo biến mới u (u = u(x)) thì sau khi tính nguyên hàm, ta phải trở lại biến x ban đầu bằng cách thay u bởi u(x).
2. Phương pháp tính nguyên hàm từng phần.
- Định lí 2.
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
- Chú ý.
Vì u’(x) dx = du; v’(x) dx = dv. Nên đẳng thức trên còn được viết ở dạng:
Đó là công thức nguyên hàm từng phần.
CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
1. Dạng trong đó m, n là các số tự nhiên.
Trường hợp 1: Trong hai số m, n có ít nhất một số lẻ.
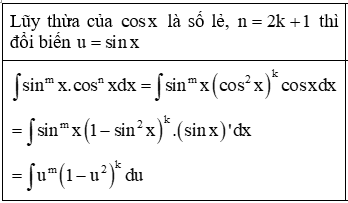
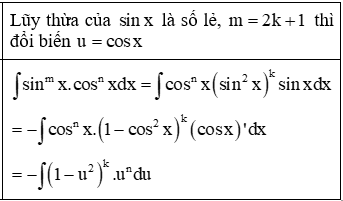
Trường hợp 2: Cả hai số m, n đều là số chẵn: Ta sử dụng công thức hạ bậc để giảm một nửa số mũ của , để làm bài toán trở nên đơn giản hơn.
2. Dạng ;
; ;
.
Ta sử dụng công thức biến đổi tích thành tổng trong lượng giác.
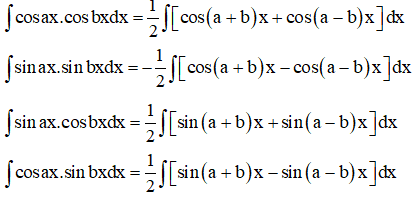
3. Dạng trong đó m, n là các số nguyên.

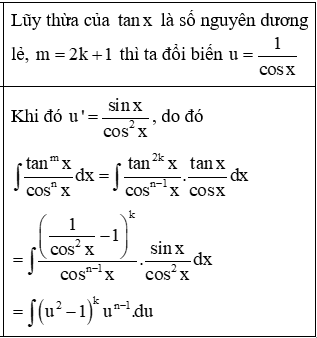
4. Đổi biến số với hàm lượng giác.
Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các dạng , thì ta có cách biến đổi lượng giác như sau:

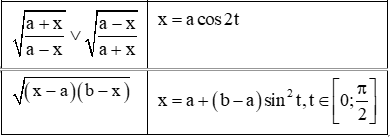
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f(x) liên tục trên R. Gọi là hai nguyên hàm của f(x) trên R thỏa mãn và . Khi đó bằng
Cho hàm số f(x) liên tục trên R. Gọi là hai nguyên hàm của f(x) trên R thỏa mãn và . Khi đó bằng
Câu 3:
Có bao nhiêu giá trị nguyên của tham số m để hàm số có ba điểm cực trị?
Có bao nhiêu giá trị nguyên của tham số m để hàm số có ba điểm cực trị?
Câu 4:
Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh được đánh số từ 1 đến 9. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh được đánh số từ 1 đến 9. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
Câu 5:
Cho hàm số có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
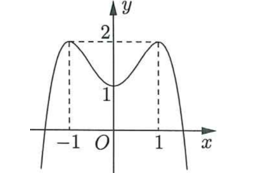
Cho hàm số có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

Câu 6:
Trong không gian Oxyz, cho điểm và đường thẳng . Gọi (P) là mặt phẳng đi qua A và chứa d. Khoảng cách từ điểm đến (P) bằng
Trong không gian Oxyz, cho điểm và đường thẳng . Gọi (P) là mặt phẳng đi qua A và chứa d. Khoảng cách từ điểm đến (P) bằng
Câu 7:
Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường và y=0quanh trục Ox bằng
Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường và y=0quanh trục Ox bằng
Câu 8:
Trong không gian Oxyz, góc giữa hai mặt phẳng (Oxy) và (Oyz)bằng
Câu 9:
Cho hàm số có đạo hàm liên tục trên R và thỏa mãn. Diện tích hình phẳng giới hạn bởi các đường và bằng
Cho hàm số có đạo hàm liên tục trên R và thỏa mãn. Diện tích hình phẳng giới hạn bởi các đường và bằng
Câu 11:
Cho mặt phẳng (P) tiếp xúc với mặt cầu S(O,R). Gọi d là khoảng cách từ O đến (P). Khẳng định nào dưới đây đúng?
Cho mặt phẳng (P) tiếp xúc với mặt cầu S(O,R). Gọi d là khoảng cách từ O đến (P). Khẳng định nào dưới đây đúng?
Câu 12:
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng (0,1)?
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng (0,1)?
Câu 13:
Cho hình nón có đường kính đáy 2r và độ dải đường sinh l . Diện tích xung quanh của hình nón đã cho bằng
Câu 14:
Cho hàm số có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là




![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)