Câu hỏi:
13/11/2024 10,498
Cho hình nón có đường kính đáy 2r và độ dải đường sinh l . Diện tích xung quanh của hình nón đã cho bằng
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C
*Lời giải:
Hình nón có đường kính đáy 2r nên nó có bán kính đáy bằng l. Vậy diện tích xung quanh của hình nón đã cho bằng
*Phương pháp giải:
Hình nón có chiều cao là h, bán kính đáy r và độ dài đường sinh là l
- Diện tích xung quanh:
*Lý thuyến cần nắm và dạng toán về hình nón:
Thiết diện khi cắt bởi mặt phẳng
a. Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh thì có các trường hợp sau xảy ra:
- Mặt phẳng (Q) cắt mặt nón theo 2 đường sinh thì thiết diện là tam giác cân
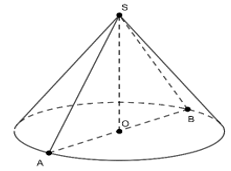
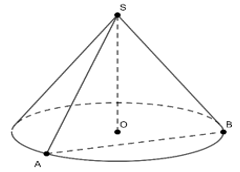
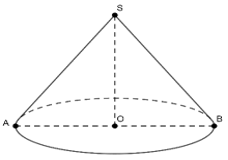
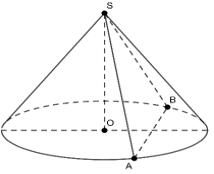
Trên hình vẽ thiết diện là tam giác SAB
- Mặt phẳng (Q) tiếp xúc với mặt nón theo 1 đường sinh thì (Q) là mặt phẳng tiếp diện của hình nón
b. Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh thì có các trường hợp sau xảy ra:
- Mặt phẳng (Q) vuông góc với trục hình nón thì giao tuyến là 1 đường tròn
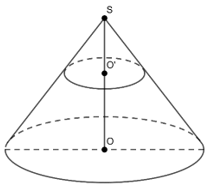
Trên hình vẽ, thiết diện là đường tròn tâm O’
- Mặt phẳng (Q) song song với 2 đường sinh hình nón thì giao tuyến là 2 nhánh của một hypebol
- Mặt phẳng (Q) song song với 1 đường sinh hình nón thì giao tuyến là 1 đường parabol
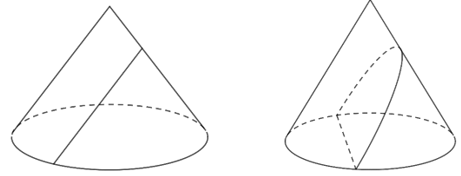
- Mặt phẳng (Q) cắt mọi đường sinh hình nón thì giao tuyến là một đường elip
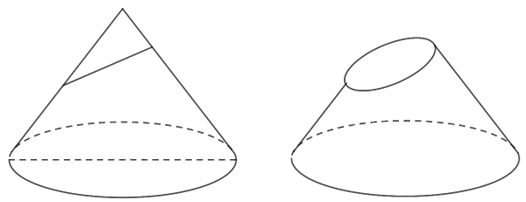
Diện tích hình nón và thể tích khối nón.
Một hình chóp gọi là nội tiếp hình nón nếu:
- Đáy của hình chóp là đa giác nội tiếp đáy của hình nón
- Đỉnh của hình chóp là đỉnh của hình nón
Diện tích xung quanh, diện tích toàn phần của hình nón.
Hình nón có chiều cao là h, bán kính đáy r và độ dài đường sinh là l
- Diện tích xung quanh:
- Diện tích đáy:
- Diện tích toàn phần:
Thể tích của khối nón:
- Thể tích của khối nón có bán kính r và chiều cao h là:
Mối liên hệ giữa chiều cao, đường sinh và bán kính đáy
Tam giác SAO vuông tại A, có
Do đó: (tham khảo hình vẽ dưới)
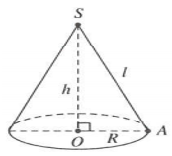
Các dạng bài tập
Dạng 1: Tính diện tích xung quanh, diện tích toàn phần, thể tích
Phương pháp giải: Sử dụng công thức:
Diện tích xung quanh hình nón:
Diện tích toàn phần hình nón:
Thể tích khối nón:
Trong đó: h là chiều cao, r là bán kính đáy và l độ dài đường sinh của hình nón.
Dạng 2: Tương giao giữa nón và mặt phẳng, bài toán thiết diện
Phương pháp giải:
a. Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh thì có các trường hợp sau xảy ra:
- Mặt phẳng (Q) cắt mặt nón theo 2 đường sinh thì thiết diện là tam giác cân
- Mặt phẳng (Q) tiếp xúc với mặt nón theo 1 đường sinh thì (Q) là mặt phẳng tiếp diện của hình nón
b. Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh thì có các trường hợp sau xảy ra:
- Mặt phẳng (Q) vuông góc với trục hình nón thì giao tuyến là 1 đường tròn
- Mặt phẳng (Q) song song với 2 đường sinh hình nón thì giao tuyến là 2 nhánh của một hypebol
- Mặt phẳng (Q) song song với 1 đường sinh hình nón thì giao tuyến là 1 đường parabol
- Mặt phẳng (Q) cắt mọi đường sinh hình nón thì giao tuyến là một đường elip
Dạng 3: Sự tạo thành nón
Phương pháp giải: Sử dụng định nghĩa mặt nón, hình nón, khối nón và các công thức liên quan.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Ôn tập chương 2 (mới 2024 + Bài Tập) – Toán 12
50 bài toán về mặt nón và phương pháp giải bài tập (có đáp án 2024) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f(x) liên tục trên R. Gọi là hai nguyên hàm của f(x) trên R thỏa mãn và . Khi đó bằng
Cho hàm số f(x) liên tục trên R. Gọi là hai nguyên hàm của f(x) trên R thỏa mãn và . Khi đó bằng
Câu 3:
Có bao nhiêu giá trị nguyên của tham số m để hàm số có ba điểm cực trị?
Có bao nhiêu giá trị nguyên của tham số m để hàm số có ba điểm cực trị?
Câu 4:
Cho hàm số có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
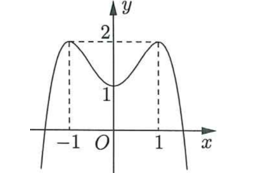
Cho hàm số có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

Câu 5:
Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh được đánh số từ 1 đến 9. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh được đánh số từ 1 đến 9. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
Câu 6:
Trong không gian Oxyz, cho điểm và đường thẳng . Gọi (P) là mặt phẳng đi qua A và chứa d. Khoảng cách từ điểm đến (P) bằng
Trong không gian Oxyz, cho điểm và đường thẳng . Gọi (P) là mặt phẳng đi qua A và chứa d. Khoảng cách từ điểm đến (P) bằng
Câu 7:
Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường và y=0quanh trục Ox bằng
Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường và y=0quanh trục Ox bằng
Câu 8:
Trong không gian Oxyz, góc giữa hai mặt phẳng (Oxy) và (Oyz)bằng
Câu 9:
Cho hàm số có đạo hàm liên tục trên R và thỏa mãn. Diện tích hình phẳng giới hạn bởi các đường và bằng
Cho hàm số có đạo hàm liên tục trên R và thỏa mãn. Diện tích hình phẳng giới hạn bởi các đường và bằng
Câu 10:
Cho mặt phẳng (P) tiếp xúc với mặt cầu S(O,R). Gọi d là khoảng cách từ O đến (P). Khẳng định nào dưới đây đúng?
Cho mặt phẳng (P) tiếp xúc với mặt cầu S(O,R). Gọi d là khoảng cách từ O đến (P). Khẳng định nào dưới đây đúng?
Câu 12:
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng (0,1)?
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng (0,1)?
Câu 13:
Cho hàm số có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là

Câu 15:
Trong không gian Oxyz cho Xét các điểm M thay đổi sao cho tam giácOAM không có góc tù và có diện tích bằng 15 Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?
Trong không gian Oxyz cho Xét các điểm M thay đổi sao cho tam giácOAM không có góc tù và có diện tích bằng 15 Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)