Câu hỏi:
10/12/2024 56,938
Có bao nhiêu cặp số nguyên (x,y) thỏa mãn
log3(x2+y2+x)+log2(x2+y2)≤log3x+log2(x2+y2+24x)?
Có bao nhiêu cặp số nguyên (x,y) thỏa mãn
log3(x2+y2+x)+log2(x2+y2)≤log3x+log2(x2+y2+24x)?A. 89
B. 48
C. 90
D. 49
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là B
Lời giải
Điều kiện: x>0.
Ta có: log3(x2+y2+x)+log2(x2+y2)≤log3x+log2(x2+y2+24x)
⇔log3(x2+y2+x)−log3x≤log2(x2+y2+24x)−log2(x2+y2)
⇔log3(x2+y2+xx)≤log2(x2+y2+24xx2+y2)⇔log3(1+x2+y2x)≤log2(1+24xx2+y2)
⇔log3(x2+y2x+1)−log2(1+24xx2+y2)≤0.
Đặt: t=x2+y2x(t>0), bất phương trình trở thành: log3(1+t)−log2(1+24t)≤0 (1).
Xét hàm số f(t)=log3(1+t)−log2(1+24t) có f'.
Suy ra hàm số đồng biến trên khoảng .
Ta có
Từ đó suy ra: .
Đếm các cặp giá trị nguyên của
Ta có: , mà x>0 nên .
Với nên có 10 cặp.
Với nên có 14 cặp.
Với nên có 14 cặp.
Với nên có 9 cặp.
Với có 1 cặp.
Vậy có 48 cặp giá trị nguyên thỏa mãn đề bài.
*Phương pháp giải:
Xét bất phương trình logaf(x) > logag(x) (a > 0, a ≠ 1)
• Nếu a > 1 thì logaf(x) > logag(x) ⇔ f(x) > g(x) (cùng chiều khi a > 1)
• Nếu 0 < a < 1 thì logaf(x) > logag(x) ⇔ f(x) < g(x) (ngược chiều khi 0 < a < 1 )
• Nếu a chứa ẩn thì logaf(x) > logag(x) ⇔ 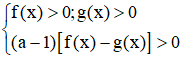 (hoặc chia 2 trường hợp của cơ số)
(hoặc chia 2 trường hợp của cơ số)
*Lý thuyết:
1. Định nghĩa
Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
2. Phương trình và bất phương trình lôgarit cơ bản: cho a,b > 0, a ≠ 1
Bất phương trình lôgarit cơ bản có dạng: logaf(x) > b; logaf(x) ≥ b; logaf(x) < b; logaf(x) ≤ b
3. Phương pháp giải phương trình và bất phương trình lôgarit
+ Đưa về cùng cơ số
Nếu 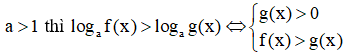
Nếu 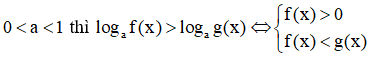
+ Đặt ẩn phụ
+ Mũ hóa
+ Phương pháp hàm số và đánh giá
Xem thêm
Bất phương trình logarit và cách giải các dạng bài tập (2024)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f(x) liên tục trên R. Gọi là hai nguyên hàm của f(x) trên R thỏa mãn và . Khi đó bằng
Cho hàm số f(x) liên tục trên R. Gọi là hai nguyên hàm của f(x) trên R thỏa mãn và . Khi đó bằng
Câu 2:
Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh được đánh số từ 1 đến 9. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh được đánh số từ 1 đến 9. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
Câu 3:
Có bao nhiêu giá trị nguyên của tham số m để hàm số có ba điểm cực trị?
Có bao nhiêu giá trị nguyên của tham số m để hàm số có ba điểm cực trị?
Câu 4:
Cho hàm số có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
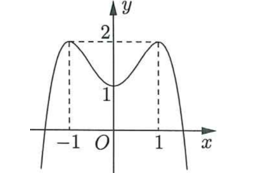
Cho hàm số có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

Câu 5:
Trong không gian Oxyz, cho điểm và đường thẳng . Gọi (P) là mặt phẳng đi qua A và chứa d. Khoảng cách từ điểm đến (P) bằng
Trong không gian Oxyz, cho điểm và đường thẳng . Gọi (P) là mặt phẳng đi qua A và chứa d. Khoảng cách từ điểm đến (P) bằng
Câu 6:
Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường và y=0quanh trục Ox bằng
Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường và y=0quanh trục Ox bằng
Câu 7:
Trong không gian Oxyz, góc giữa hai mặt phẳng (Oxy) và (Oyz)bằng
Câu 8:
Cho hàm số có đạo hàm liên tục trên R và thỏa mãn. Diện tích hình phẳng giới hạn bởi các đường và bằng
Cho hàm số có đạo hàm liên tục trên R và thỏa mãn. Diện tích hình phẳng giới hạn bởi các đường và bằng
Câu 10:
Cho mặt phẳng (P) tiếp xúc với mặt cầu S(O,R). Gọi d là khoảng cách từ O đến (P). Khẳng định nào dưới đây đúng?
Cho mặt phẳng (P) tiếp xúc với mặt cầu S(O,R). Gọi d là khoảng cách từ O đến (P). Khẳng định nào dưới đây đúng?
Câu 11:
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng (0,1)?
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng (0,1)?
Câu 12:
Cho hình nón có đường kính đáy 2r và độ dải đường sinh l . Diện tích xung quanh của hình nón đã cho bằng
Câu 13:
Cho hàm số có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là

Câu 15:
Trong không gian Oxyz cho Xét các điểm M thay đổi sao cho tam giácOAM không có góc tù và có diện tích bằng 15 Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?
Trong không gian Oxyz cho Xét các điểm M thay đổi sao cho tam giácOAM không có góc tù và có diện tích bằng 15 Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)