Xét dấu của biểu thức f(x) = 2x(x + 2) - (x + 2)(x + 1)

Với giải Bài 6 trang 160 sgk Toán lớp 10 Đại số được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

1 3898 lượt xem

Trang trước

Trang sau

Giải Toán 10 Ôn tập cuối năm

Video Giải Bài 6 trang 160 Toán lớp 10 Đại số

Bài 6 trang 160 Toán lớp 10 Đại số:

a) Xét dấu của biểu thức f(x) = 2x(x + 2) - (x + 2)(x + 1)

b) Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các đồ thị của các hàm số sau

y = 2x(x+2) ( C₁)

y = (x+2)(x+1)(C₂)

Tính tọa độ giao điểm A và B của (C₁) và (C₂).

c) Tính các hệ số a, b, c để hàm số y = ax² + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.

Lời giải

a) f(x) = 2x.(x + 2) - (x + 2)(x + 1) = 2x² + 4x - (x² + 3x + 2) = x² + x - 2

Tam thức x² + x – 2 có hai nghiệm x₁ = -2 và x₂ = 1, hệ số a = 1 > 0.

Vậy:

+ f(x) > 0 nếu x > x₂ = 1 hoặc x < x₁ = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)

+ f(x) < 0 nếu x₁ < x < x₂ hay x ∈ (-2; 1)

+ f(x) = 0 nếu x = -2 hoặc x = 1.

* Hàm số y = 2x(x + 2) = 2x² + 4x có đồ thị (C₁) là parabol có:

+ Tập xác định: D = R

+ Đỉnh I₁(-1; -2)

+ Trục đối xứng: x = -1

+ Giao điểm với trục tung tại gốc tọa độ.

+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).

+ Bảng biến thiên:

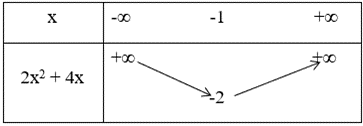
Tài liệu VietJack

* Hàm số y = (x + 2)(x+1) = x² + 3x + 2 có đồ thị (C₂) là parabol có:

+ Tập xác định D = R.

+ Đỉnh $I (\frac{- 3}{2}; \frac{- 1}{4})$

+ Trục đối xứng: x = $\frac{- 3}{2}$

+ Giao với trục tung tại D(0; 2)

+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)

+ Bảng biến thiên

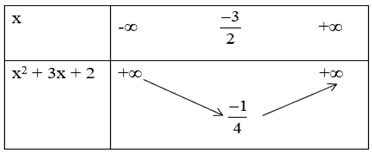
Tài liệu VietJack

* Đồ thị:

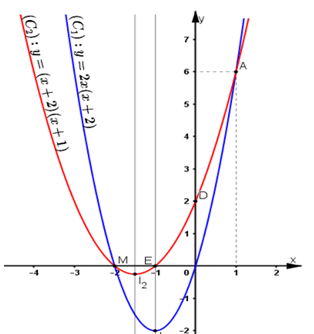
Tài liệu VietJack

* Tìm tọa độ giao điểm:

Cách 1: Dựa vào đồ thị hàm số:

Nhìn vào đồ thị thấy (C₁) cắt (C₂) tại A(1; 6) và B ≡ M(-2; 0)

Cách 2: Tính:

Hoành độ giao điểm của (C₁) và (C₂) là nghiệm của phương trình:

2x(x + 2) = (x + 2)(x + 1)

⇔ (x + 2).2x – (x + 2)(x + 1) = 0

⇔ (x + 2).(2x – x – 1) = 0

⇔ (x + 2).(x – 1) = 0

⇔ x = -2 hoặc x = 1.

+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)

+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).

+ Đồ thị hàm số y = ax² + bx + c đi qua điểm A(1; 6) và B(-2; 0)

⇔ Tọa độ A và B thỏa mãn phương trình y = ax² + bx + c

$\Leftrightarrow \{\begin{cases} a + b + c = 0 \\ 4 a - 2 b + c = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} b + x = 6 - a \\ - 2 b + c = - 4 a \end{cases}$

$\Leftrightarrow \{\begin{cases} 3 b = 6 + 3 a \\ c = - 4 a + 2 b \end{cases}$

$\Leftrightarrow \{\begin{cases} b = 2 + a \\ c = 4 - 2 a \end{cases}$

+ Ta có bảng biến thiên của hàm số y = ax² + bx + c:

Nếu a < 0

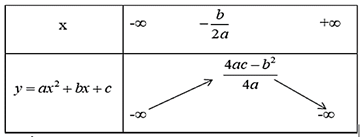
Tài liệu VietJack

Nếu a > 0

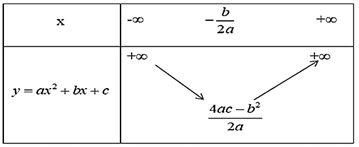
Tài liệu VietJack

Nhận thấy y đạt giá trị lớn nhất bằng 8

$\Leftrightarrow \{\begin{cases} \frac{4 a c - b^{2}}{4 a} = 8 \\ a < 0 \end{cases} \Leftrightarrow \{\begin{cases} 4 a c - b^{2} = 32 a \\ a < 0 \end{cases}$