TOP 6 Đề thi Học kì 1 Toán lớp 7 có đáp án hay nhất
TOP 6 Đề thi Học kì 1 Toán lớp 7 có đáp án hay nhất giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 7 Giữa học kì 1. Mời các bạn cùng đón xem:
TOP 6 Đề thi Học kì 1 Toán lớp 7 có đáp án hay nhất
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 7
Thời gian làm bài: 45 phút
(Đề số 1)
I. Phần trắc nghiệm (3 điểm) Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ −34?
A. −62
B. 8−6
C. 9−12
D. −129
Câu 2: Kết quả phép tính −38+56 là:
A. 1124
B. 2248
C. −1124
D. −2248
Câu 3: Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ k của y đối với x là:
A. 3
B. 75
C. 13
D. 10
Câu 4: Nếu góc xOy có số đo bằng 47o thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu?
A. 133o
B. 43o
C. 74o
D. 47o
Câu 5: Cho hình vẽ.
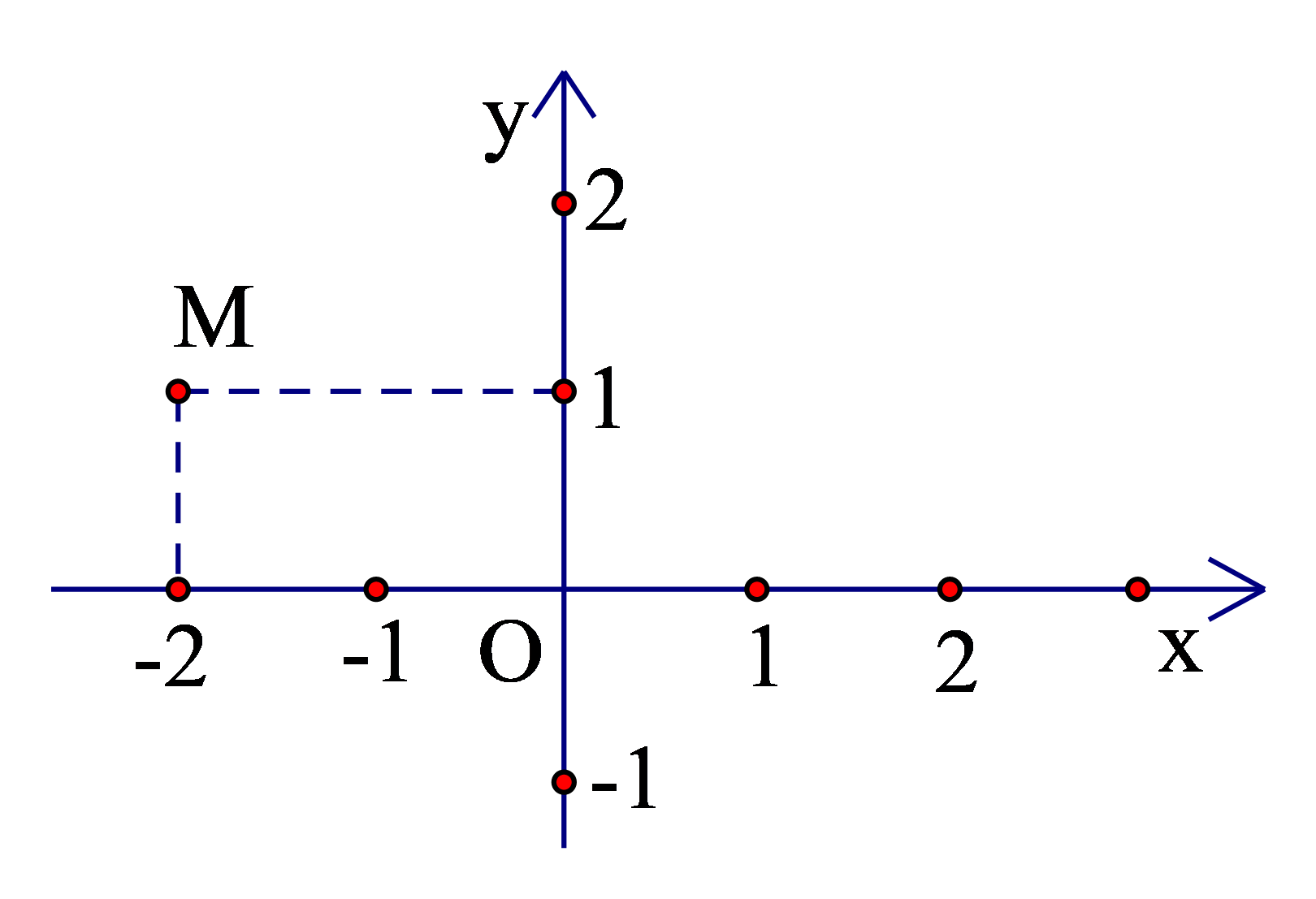 Tọa độ điểm M là:
Tọa độ điểm M là:
A. (2; −1)
B. (−2; 1)
C. (1; −2)
D. (−1; 2)
Câu 6: Cho hình vẽ sau:
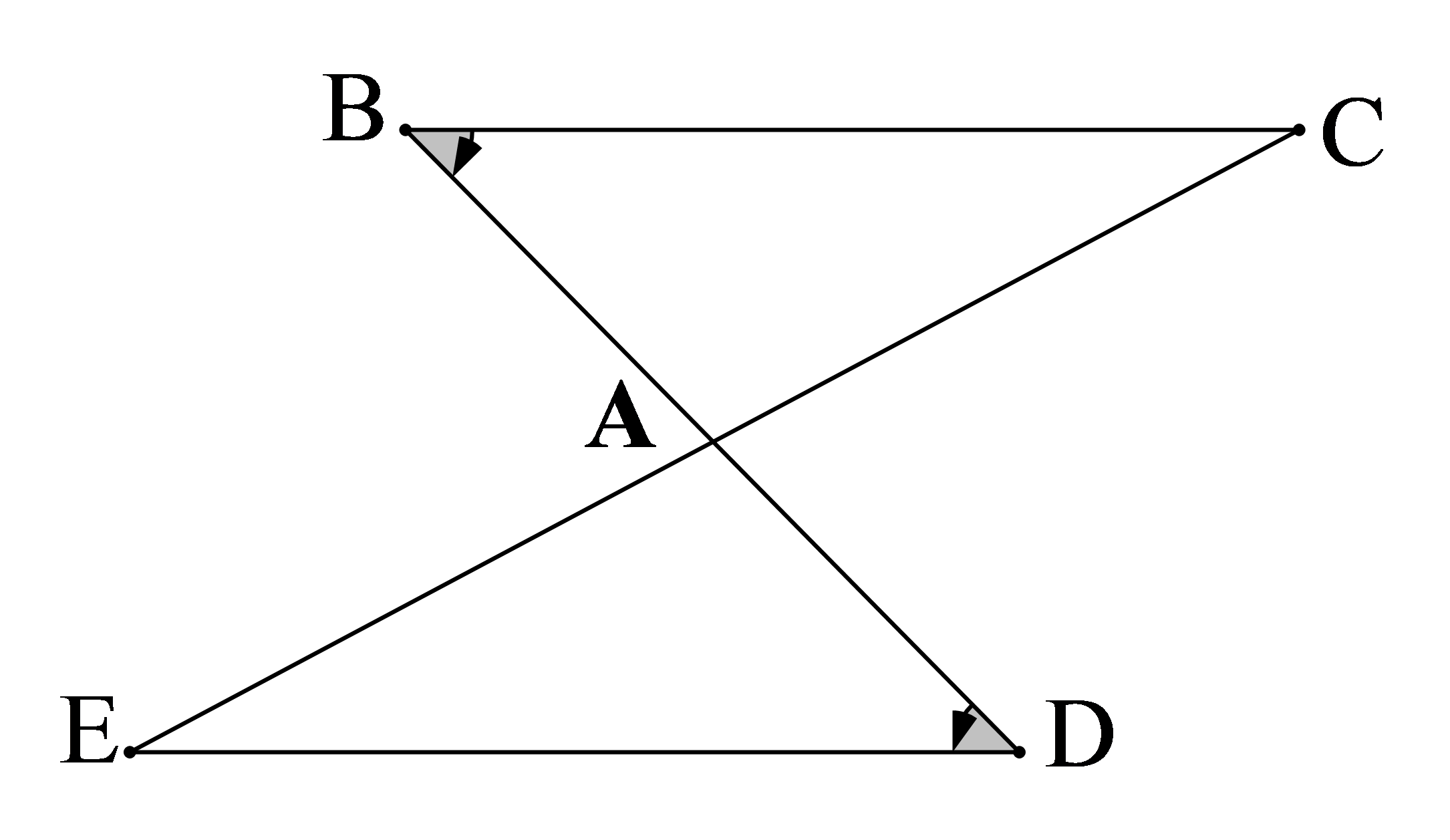
Với các kí hiệu trên hình vẽ, cần có thêm yếu tố nào nữa để kết luận ∆ABC = ∆ADE (g.c.g)?
A. BC = DE
B. AB = AD
C. AC = AE
D. ^BCA=^DEA
II. Tự luận
Bài 1 (1 điểm): Thực hiện phép tính (tính bằng cách hợp lý nếu có thể)
a) −112 . 2113+112 . 113
b) (−2)35 . |14−1|+20180.
Bài 2 (1,5 điểm): Tìm x, biết:
a) (0,5x−37):12=117
b) |2 − 3x| − 5 = −1
c) (15−32x)2=94.
Bài 3 (1,5 điểm): Một tam giác có chu vi bằng 36cm, ba cạnh của tam giác đó lần lượt tỉ lệ thuận với 3; 4; 5. Tính độ dài ba cạnh của tam giác đó.
Bài 4 (2,5 điểm): Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.
a) Chứng minh: ∆OAD = ∆OCB.
b) Chứng minh: IA = IC.
c) Chứng minh: OI là tia phân giác của ^xOy.
Bài 5 (0,5 điểm): Tìm x, y biết: 1+3y12=1+5y5x=1+7y4x.
Đáp án
I. Phần trắc nghiệm (3 điểm)
Câu 1: C
Giải thích: Rút gọn các phân số ở các đáp án A, B, C, D, ta được:
A. −62=−3
B. 8−6=−43
C. 9−12=−34
D. −129=−43
Vậy chọn C. 9−12.
Câu 2: A
Giải thích:
Ta có: −38+56=−924+2024=−9+2024=1124.
Câu 3 A
Giải thích: Công thức liên hệ của hai đại lượng x, y tỉ lệ thuận: y = k . x (với k là hệ số tỉ lệ).
Do đó k=yx=155=3.
Câu 4: D
Giải thích: Dựa vào tính chất: Hai góc đối đỉnh thì bằng nhau.
Ta có góc xOy có số đo bằng 47o nên góc đối đỉnh với góc xOy cũng có số đo bằng 47o.
Câu 5: B
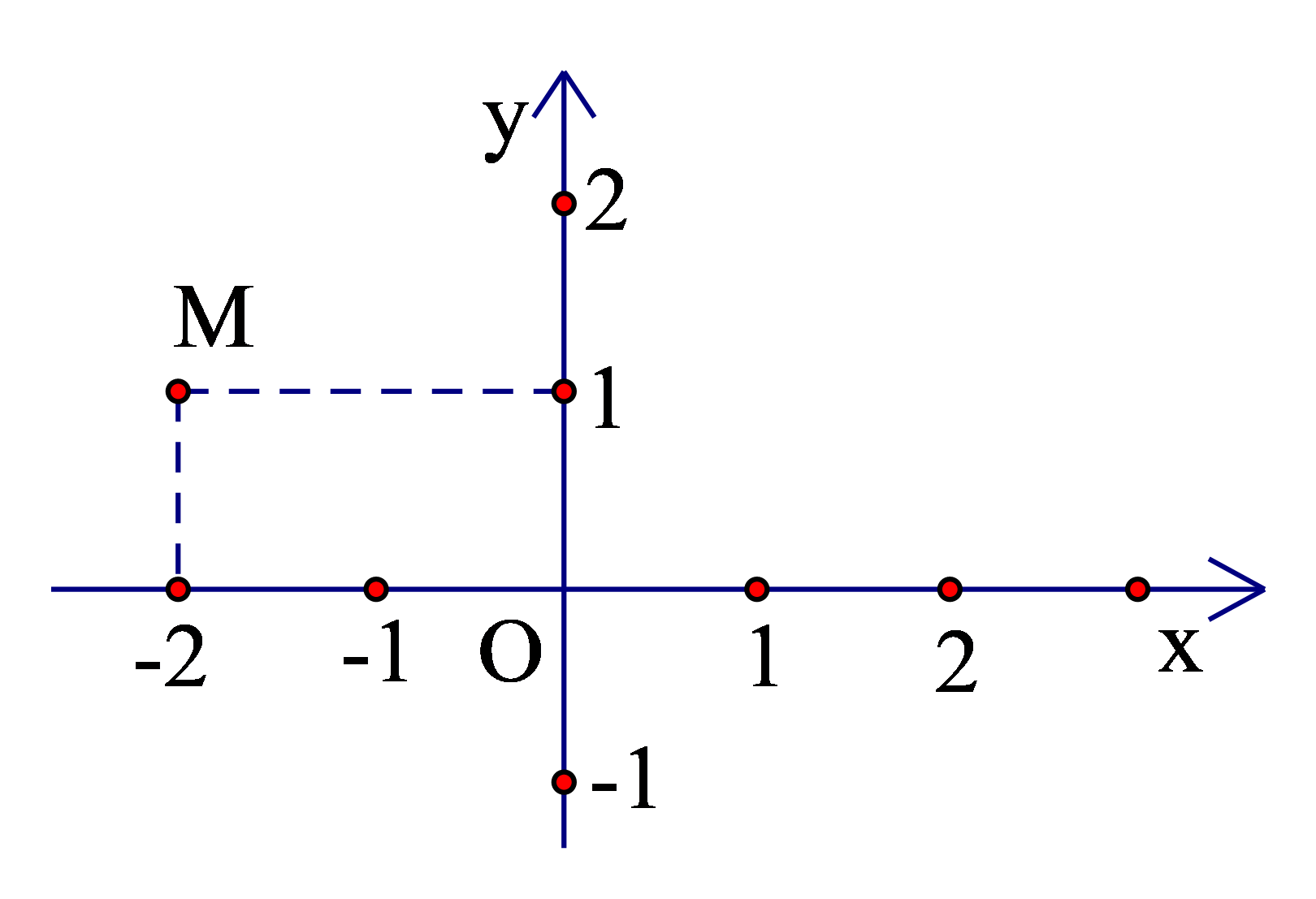
Giải thích: Dựa vào đồ thị hàm số, ta thấy điểm M có hoành độ bằng −2 và tung độ bằng 1.
Do đó, điểm M (−2; 1).
Câu 6: B
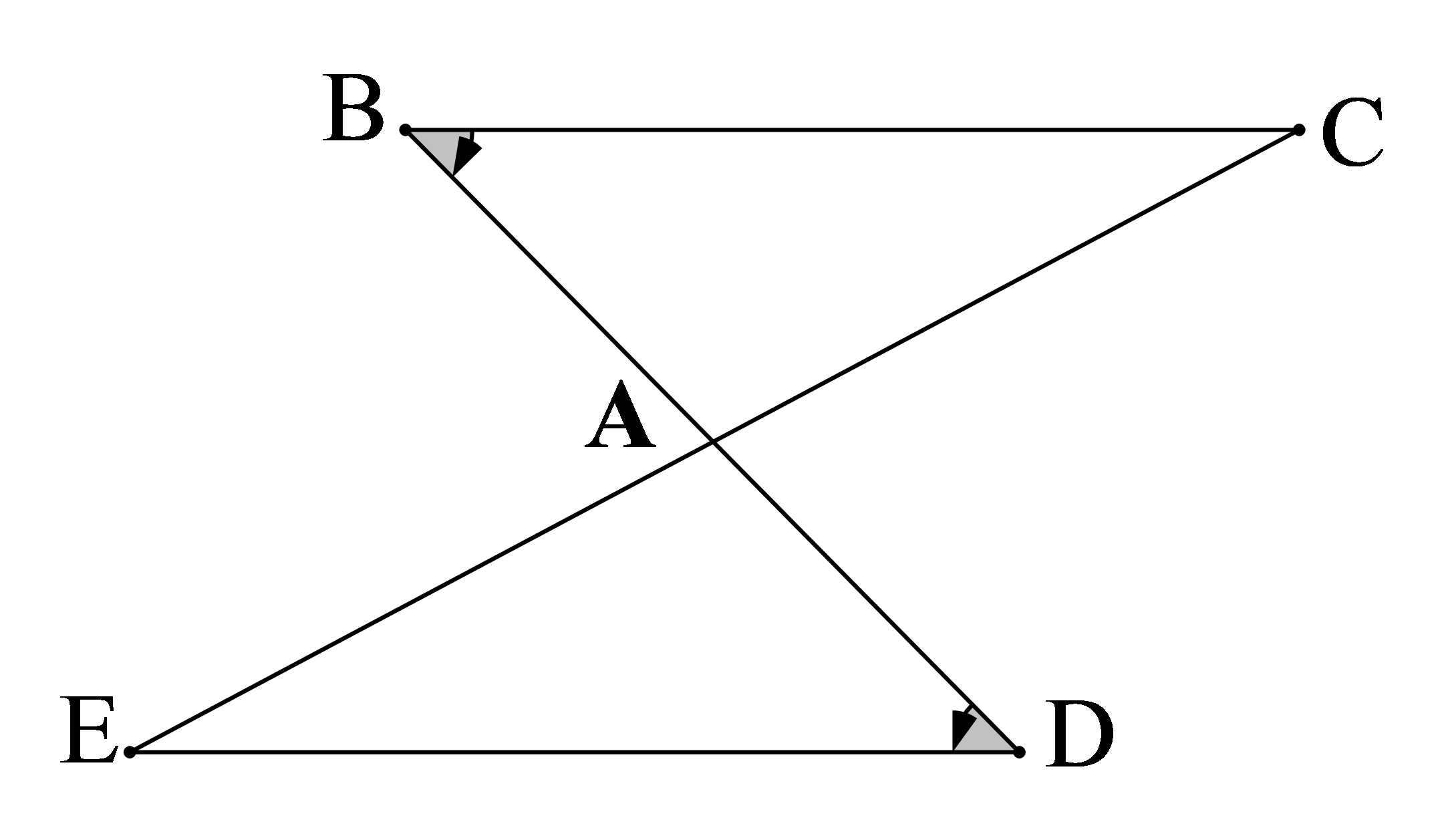 Giải thích: Trong hình vẽ trên có ^ABC=^ADC
Giải thích: Trong hình vẽ trên có ^ABC=^ADC
Ta lại có ^BAC=^DAE (hai góc đối đỉnh).
Để ∆ABC = ∆ADE (g.c.g) thì ta cần tìm thêm một điều kiện về cạnh thỏa mãn:
+ Cạnh xen giữa hai góc: Cạnh AB xen giữa hai góc ^ABC và ^BAC; cạnh AD xen giữa hai góc ^ADC và ^DAE.
+ Hai cạnh đó (thuộc hai tam giác) bằng nhau: Cạnh AB thuộc ∆ABC và cạnh AD thuộc ∆ADE.
Do đó, AB = AD.
II. Tự luận
Bài 1 (1 điểm):
a) −112 . 2113+112 . 113
=−112 . (2113−113)
=−112 . 20 = −30.
b)
(−2)35 . |14−1|+20180=−85 . |−34|+1=−85 . 34+1=−65+1=−15
Bài 2 (2 điểm):
a)
(0,5 x−37):12=1170,5 x−37=117 . 120,5x−37=87 . 120,5x−37=470,5x=47+37
0,5x = 1
x = 1 : 0,5
x = 2.
Vậy x = 2.
b) |2 − 3x| − 5 = −1
|2 − 3x| = 5 −1
|2 − 3x| = 4
Trường hợp 1: 2 − 3x = 4
3x = 2 − 4
3x = −2
x=−23.
Trường hợp 2: 2 − 3x = −4
3x = 2 + 4
3x = 6
x = 2.
Vậy x∈{−23; 2}.
c) (15−32x)2=94
Trường hợp 1:
15−32x=32
32x=15−3232x=210−151032x=−1310x=−1310:32x=−1315
Trường hợp 2:
15−32x=−3232x=15+3232x=1710x=1710:32x=1715.
Vậy x∈{−1315; 1715}.
Bài 3 (1,5 điểm):
Gọi độ dài ba cạnh của tam giác là a, b, c (cm) (a, b, c > 0).
Chu vi của tam giác bằng 36 cm nên ta có: a + b + c = 36.
Giả sử ba cạnh tỉ lệ thuận với 3; 4; 5 lần lượt là a, b, c.
Khi đó: a3=b4=c5.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
a3=b4=c5=a+b+c3+4+5=3612=3
=> a = 3 . 3 = 9;
=> b = 3 . 4 = 12;
=> c = 3 . 5 = 15.
Vậy độ dài ba cạnh của tam giác là: 9 cm; 12 cm; 15 cm.
Bài 4 (2,5 điểm):
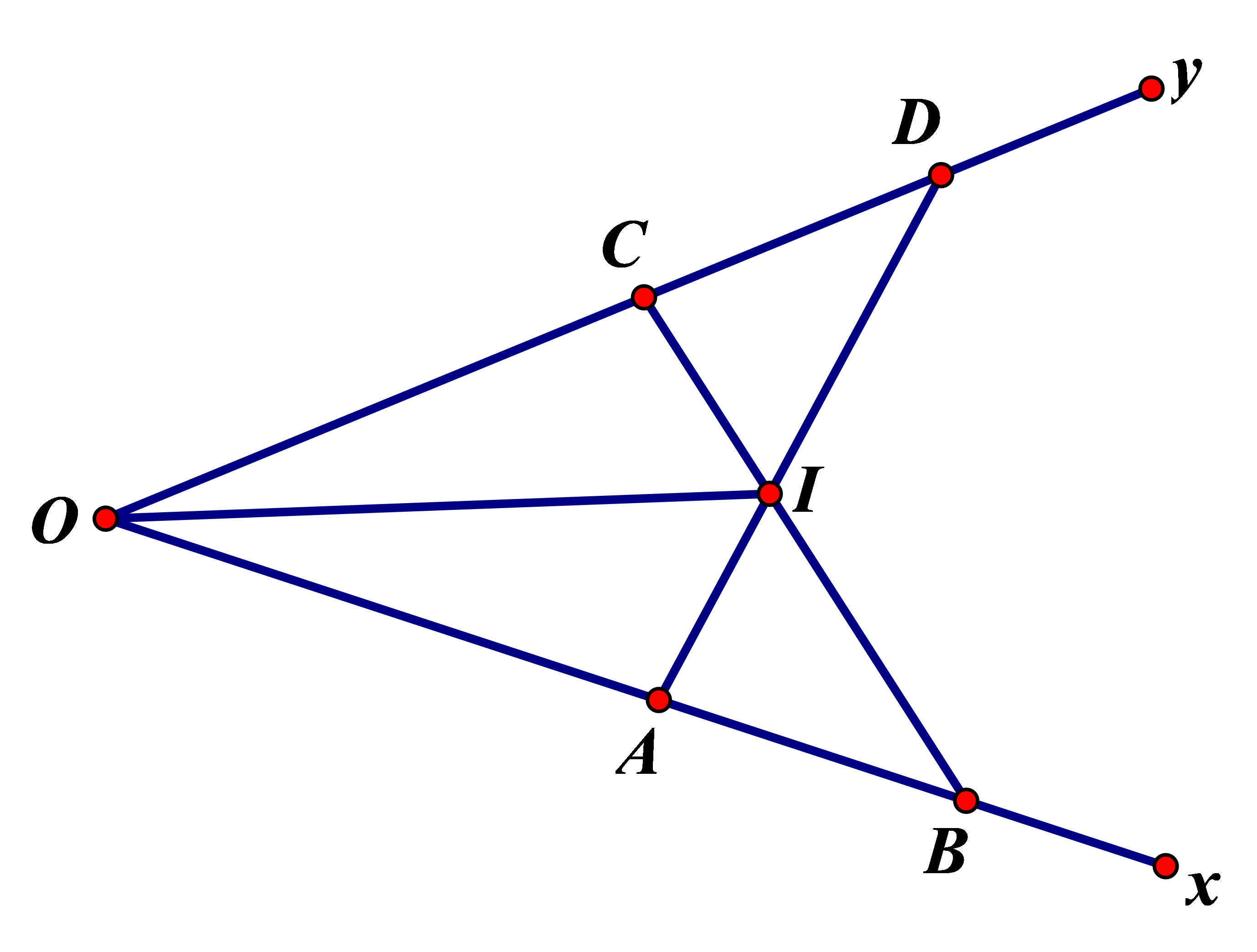
|
GT |
^xOy nhọn OA = 3 cm, OB = 5cm (A ∈ Ox, B ∈ Ox) OC = OA, OD = OB (C ∈ Oy, D ∈ Oy) AD ∩ BC=I |
|
KL |
a) ∆OAD = ∆OCB. b) IA = IC. c) OI là tia phân giác của ^xOy. |
a) Chứng minh: ∆OAD = ∆OCB.
Ta có: OA + AB = OB
OC + CD = OD
Mà OA = OC = 3cm, OD = OB = 5cm.
Nên AB = CD.
Xét ∆OAD và ∆OCB có:
OD = OB (gt)
^AOD chung
OA = OC (gt).
Do đó ∆OAD = ∆OCB (c.g.c).
b) Chứng minh: IA = IC.
∆OAD = ∆OCB (câu a)
Suy ra: ^OCB=^OAD,^OBC=^ODA (các cặp góc tương ứng).
Ta có: ^OCB+^BCD=180o
^OAD+^BAD=180o
Mà ^OCB=^OAD
Do đó: ^BCD=^BAD.
Xét ∆ICD và ∆IAB có:
^OBC=^ODA (cmt)
CD = AB (cmt)
^BCD=^BAD (cmt)
Do đó ∆ICD = ∆IAB (g.c.g).
Suy ra IA = IC (hai cạnh tương ứng).
c) Chứng minh: OI là tia phân giác của ^xOy.
Xét ∆OIC và ∆OAI có:
OC = OA (gt)
IC = IA (cmt)
Cạnh OI chung
Do đó ∆OIC = ∆OAI (c.c.c).
Suy ra: ^IOD=^IOB (hai góc tương ứng).
Vậy OI là tia phân giác của ^xOy.
Bài 5 (0,5 điểm): ĐK: x ![]() 0.
0.
Ta có: 1+3y12=1+5y5x=1+7y4x (*)
Suy ra: 1+3y12=1+5y5x và 1+5y5x=1+7y4x.
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
1+3y12=1+5y5x=1+3y−(1+5y)12−5x=1+3y−1−5y12−5x=−2y12−5x (1)
1+5y5x=1+7y4x=1+5y−(1+7y)5x−4x=1+5y−1−7y5x−4x=−2yx (2)
Từ (1) và (2) suy ra: −2y12−5x = −2yx (3)
- Nếu y = 0 thay vào (*), ta được: 112=15x=14x
Mà x ≠0 nên không có giá trị x thỏa mãn (*).
- Nếu y ≠0:
Từ (3) suy ra: x = 12 – 5x
x + 5x = 12
6x = 12
x = 2 (thỏa mãn)
Thay x = 2 vào (*) ta được:
1+3y12=1+5y10=1+7y8
⇒112+14y=110+12y
⇒14y=−160
⇒y=−115 (thỏa mãn)
Vậy x = 2, y=−115 thoả mãn yêu cầu bài toán.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 7
Thời gian làm bài: 45 phút
(Đề số 2)
I. Phần trắc nghiệm (3 điểm) Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Biết 2x = 8, thì giá trị x bằng:
A. 4
B. 2
C. 3
D. 6
Câu 2: Từ tỉ lệ thức 1,5x=32 thì giá trị x bằng:
A. 1
B. 2
C. 3
D. 4
Câu 3: Cho hàm số y = f (x) = 2x + 1. Khi đó f (–1) bằng:
A. 1
B. –1
C. 3
D. –3
Câu 4: Cho hai đại lượng y tỉ lệ nghịch với x theo hệ số tỉ lệ là a, nếu x = 3 thì y = 6. Vậy hệ số tỉ lệ a bằng:
A. 2
B. 0,5
C. 18
D. 3
Câu 5: Cho hình vẽ. Biết a // b. Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B sao cho ˆA1= 2 ˆB1.
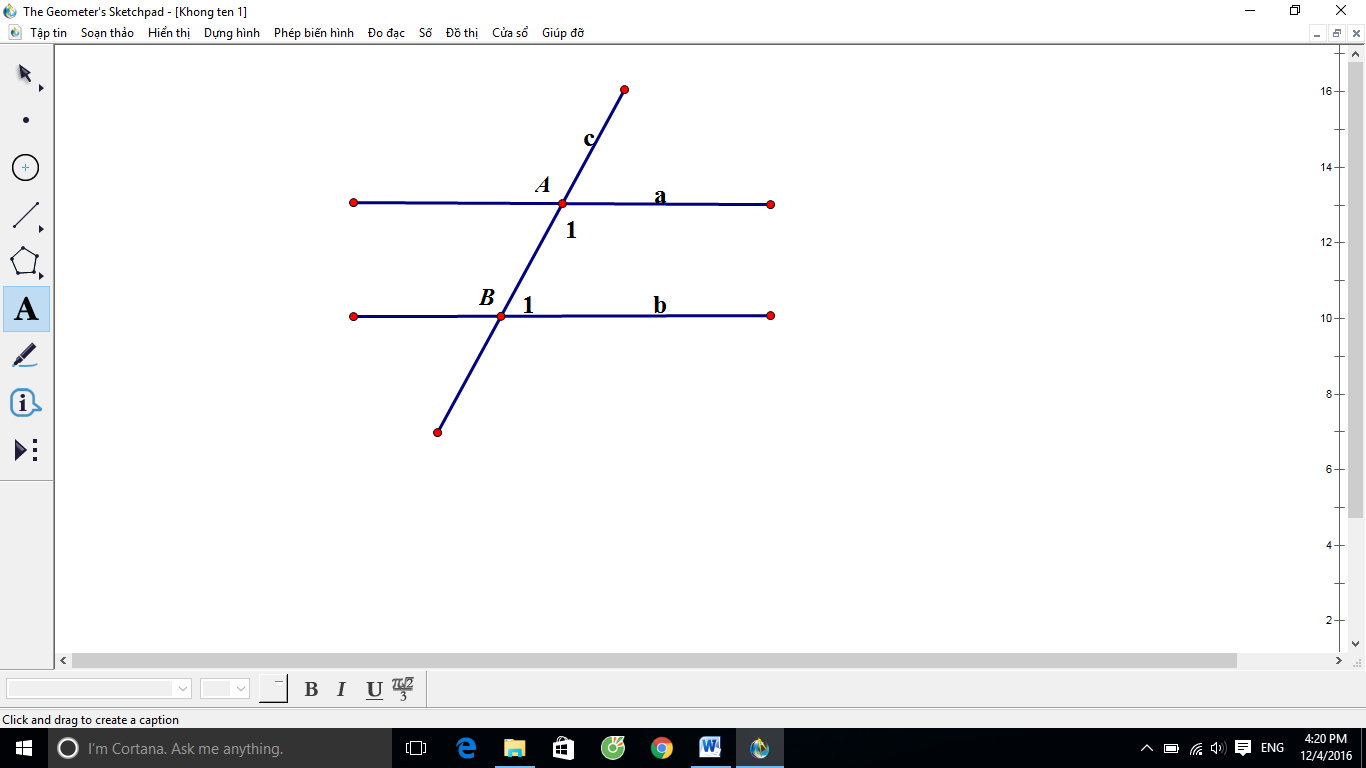 Khi đó ˆB1 bằng:
Khi đó ˆB1 bằng:
A. 60o
B. 45o
C. 75o
D. 120o
Câu 6: Cho ∆ABC = ∆MNP suy ra:
A. AB = MP
B. CB = NP
C. AC = NM
D. Cả B và C đúng.
II. Tự luận
Bài 1 (1,5 điểm): Thực hiện phép tính:
a) −25+315−13
b) 9 . (−13)2+25
c)
−43 . √416−32 . |−19|
Bài 2 (1 điểm): Tìm x biết:
a) x−23=−521
b) 13−3x=(−13)3
Bài 3 (1,5 điểm): Số học sinh lớp 7A, 7B, 7C tỉ lệ với các số 17; 18; 16. Biết rằng tổng số học sinh của cả ba lớp là 102 học sinh. Tính số học sinh của mỗi lớp.
Bài 4 (2,5 điểm): Cho ∆ABC có AB = AC; D là điểm bất kì trên cạnh AB. Tia phân giác của góc A cắt cạnh DC ở M, cắt cạnh BC ở I.
a) Chứng minh CM = BM.
b) Chứng minh AI là đường trung trực của đoạn thẳng BC.
c) Từ D kẻ DH⊥BC (H∈BC). Chứng minh ^BAC=2^ BDH.
Bài 5 (0,5 điểm): Tìm giá trị lớn nhất của biểu thức:
A = |x – 1004| – |x + 1003|.
Đáp án
I. Phần trắc nghiệm (3 điểm)
Câu 1: C
Giải thích:
Ta có: 2x = 8
2x = 23
x = 3.
Câu 3: A
Giải thích: 1,5x=32⇒x=1,5 . 23=33=1.
Câu 3: B
Giải thích: Ta có: f (–1) = 2 . (–1) + 1 = –2 + 1 = –1.
Câu 4: C
Giải thích: Công thức liên hệ của hai đại lượng x, y tỉ lệ nghịch: xy = a (với a là hệ số tỉ lệ).
Do đó: a = 3 . 6 = 18.
Câu 5: A
Giải thích: Ta có: ˆA1= 2ˆB1
Vì a // b mà ˆA1 và ˆB1 là hai góc trong cùng phía nên: ˆA1 + ˆB1 = 180o.
Khi đó, 2 ˆB1 + ˆB1 = 180o.
3ˆB1 = 180o.
Do đó: ˆB1 = 60o.
Câu 6: B
Giải thích:∆ABC = ∆MNP nên AB = MN, BC = NP, AC = MP.
Do đó các đáp án A, C, D sai; B đúng.
II. Tự luận
Bài 1 (1,5 điểm): Thực hiện phép tính:
a) −25+315−13
=−25+165−13
=145−13
=4215−515=3715;
=9 . 19+25
=1+25=125;
c) −43 . √416−32 . |−19|
=−43 . 12−9 . 19
=−23−1
=−53.
Bài 2 (1 điểm):
a) x−23=−521
x=−521+23
x=−521+1421
x=921
x=37
Vậy x=37.
b) 13−3x=(−13)3
13−3x=−127
3x=13+127
3x=1027
x=1027:3
x=1081
Vậy x=1081.
Bài 3 (1,5 điểm):
Gọi a, b, c lần lượt là số học sinh của ba lớp 7A, 7B, 7C (học sinh),
(a, b, c ∈N*, a, b, c < 102).
Vì học sinh lớp 7A, 7B, 7C tỉ lệ với các số 17; 18; 16 nên ta có
a17=b18=c16
Tổng số học sinh của cả ba lớp là 102 học sinh nên: a + b + c = 102.
Theo tính chất của dãy tỉ số bằng nhau, ta có:
a17=b18=c16=a+b+c17+18+16=10251=2
=> a = 2 . 17 = 34;
=> b = 2 . 18 = 36;
=> c = 2 . 16 = 32.
Vậy số học sinh của ba lớp 7A là 34 học sinh; 7B là 36 học sinh và 7C là 32 học sinh.
Bài 4 (2,5 điểm):
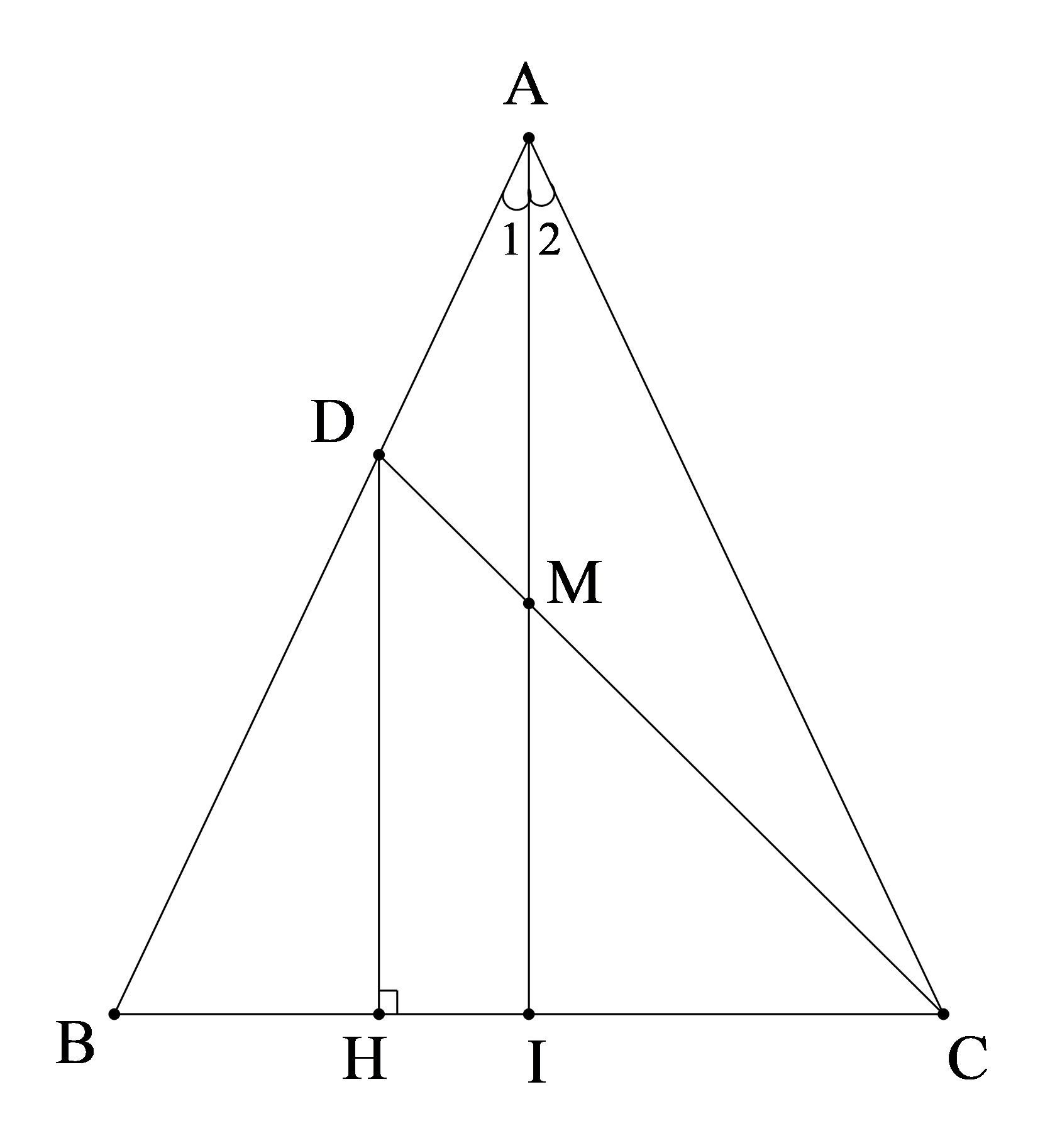
|
GT |
ΔABC, AB = AC; D ∈ AB; AI là tia phân giác của ^BAC (I ∈ BC); AI ∩ CD=M |
|
KL |
a) CM = BM. b) AI là đường trung trực của BC. c) ^BAC=2^ BDH. |
a) Chứng minh CM = BM.
Xét ΔABM và ΔACM có:
AB = AC (gt)
^BAM = ^CAM (vì AM là tia phân giác của ^BAC)
AM là cạnh chung.
Do đó ΔABM=ΔACM (c.g.c).
Suy ra BM = CM (hai cạnh tương ứng)
b) Chứng minh: AI là đường trung trực của đoạn thẳng BC.
Xét ΔABI và ΔACI có:
AB = AC (gt)
^BAI=^CAI (Vì AI là tia phân giác của ^BAC).
AI là cạnh chung.
Do đó ΔABI=ΔACI (c.g.c).
Suy ra BI = CI (hai cạnh tương ứng) (1)
Và ^AIB=^AIC (hai góc tương ứng).
Mà ^AIB+^AIC=180o (hai góc kề bù).
Nên 2 ^AIB=180o⇒^AIB=90o
Suy ra AI⊥BC (2)
Từ (1) và (2) suy ra: AI là đường trung trực của đoạn thẳng BC.
c) Chứng minh ^BAC=2^ BDH.
Ta có: DH⊥BC (gt)
AI⊥BC (cmt)
Suy ra DH // AI (quan hệ giữa tính vuông góc với tính song song).
⇒^BAI=^BDH (hai góc đồng vị) (3)
Ta lại có: ^BAI=12 ^BAC (vì AI là tia phân giác của ^BAC) (4)
Từ (3) và (4) suy ra ^BDH=12 ^BAC⇒^BAC=2^ BDH.
Vậy ^BAC=2^ BDH.
Bài 5 (0,5 điểm):
Áp dụng tính chất |x − y| ≥ |x| − |y|
A = |x – 1004| – |x + 1003| ≤ |(x – 1004) – (x + 1003)|
= |x – 1004 – x − 1003| = |–1004 − 1003| = 2007.
Vậy giá trị lớn nhất của biểu thức A là 2007.
Dấu ‘‘=’’ xảy ra khi x – 1004 ≥ 0 hoặc x + 1003 ≤ 0.
Khi đó x ≥ 1004 hoặc x ≤ –1003.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 7
Thời gian làm bài: 45 phút
(Đề số 3)
I. Phần trắc nghiệm (3 điểm) Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Tổng 36+−16 bằng:
A. 13
B. −23
C. 23
D. −13
Câu 2: Nếu √x=4 thì x bằng:
A. 2
B. 4
C. ± 2
D. 16
Câu 3: Cho hai đại lượng y tỉ lệ thuận với x theo hệ số tỉ lệ –3 thì y và x liên hệ với nhau theo công thức:
A. y = −3x
B. y = −13x
C. y = 13x
D. y = 3x
Câu 4: Nếu a⊥b và b // c thì:
A. a // c
B. a⊥c
C. b⊥c
D. a // b // c
Câu 5: Cho tam giác ABC có ˆA=30o;ˆB=50o. Số đo góc ngoài tại đỉnh C bằng:
A. 40o
B. 50o
C. 80o
D. 180o
Câu 6: Trong các điểm sau, điểm nào thuộc đồ thị hàm số y = 3x?
A. (−1; −3)
B. (−1; 3)
C. (−2; 1)
D. (−2; −1)
II. Tự luận
Bài 1 (1điểm): Thực hiện phép tính (tính hợp lý nếu có thể):
a) 38+22−38
b) 25 . 3313−25 . 813.
Bài 2 (1,5 điểm): Tìm x:
a) −35x=2110
b) (15−32x)2=94
c) |x + 1| = 4,5
Bài 3 (1,5 điểm): Lớp 7A có 48 học sinh được xếp loại giỏi, khá, trung bình. Biết rằng số học sinh giỏi, khá, trung bình lần lượt tỉ lệ với 4; 5; 3. Tính số học sinh giỏi, khá và trung bình của lớp 7A.
Bài 4 (2,5 điểm): Cho góc nhọn xOy. Trên tia Ox lấy điểm A và C sao cho OA < OC, trên tia Oy lấy điểm B và D sao cho OA = OB ; OC = OD. Gọi E là giao điểm của AD và BC.
a) Chứng minh: AD = BC.
b) Chứng minh: ∆EAC = ∆EBD.
c) Chứng minh: OE là tia phân giác của góc xOy.
Bài 5 (0,5 điểm): Cho 1c=12(1a+1b) (với a, b, c ≠ 0, b ≠ c). Chứng minh
rằng: ab=a−cc−b.
Đáp án
I. Phần trắc nghiệm (3 điểm)
Câu 1: A
Giải thích: Ta có: 36+−16=3+(−1)6=26=13.
Câu 2: D
Giải thích: Ta có √x=4 suy ra x = 42 = 16.
Câu 3: A
Giải thích: Công thức liên hệ của hai đại lượng x, y tỉ lệ thuận: y = k . x (với k là hệ số tỉ lệ).
Với hệ số tỉ lệ k = –3 thì y = −3x.
Câu 4: B
Giải thích: Vì a⊥b và b // c.
Nên a⊥b (quan hệ giữa tính vuông góc với tính song song).
Câu 5: C
Giải thích: Số đo góc ngoài tại đỉnh C bằng:
ˆA+ˆB=30o+50o=80o (tính chất góc ngoài của tam giác).
Câu 6: A
Giải thích: Thay tọa độ các điểm ở các đáp án A, B, C, D vào đồ thị hàm số y = 3x, ta có:
- Với điểm có tọa độ (−1; −3) thì 3 . (−1) = −3 nên (−1; −3) thuộc đồ thị hàm số y = 3x;
- Với điểm có tọa độ (−1; 3) thì 3 . (−1) = −3 ≠ 3 nên (−1; 3) không thuộc đồ thị hàm số y = 3x;
- Với điểm có tọa độ (−2; 1) thì 3 . (−2) = −6 ≠ 1 nên (−2; 1) không thuộc đồ thị hàm số y = 3x;
- Với điểm có tọa độ (−2; −1) thì 3 . (−2) = −6 ≠ −1 nên (−2; −1) không thuộc đồ thị hàm số y = 3x.
Vậy chọn A. (−1; −3).
II. Tự luận
Bài 1 (1điểm):
a) 38+22−38
=38−38+22
= 0 + 22
= 22 = 4.
b) 25 . 33 13−25 . 813
=25 . (3313− 813)
=25 . 25
= 10.
Bài 2 (1,5 điểm):
a) −35x=2110
x=2110:(−35)
x=2110 . −53
x=−72.
Vậy x=−72.
b) (15−32x)2=94
- Trường hợp 1: 15−32x=32
32x=15−32
32x=−1310
x=−1310:32
x=−1315
- Trường hợp 2: 15−32x=−32
32x=15+32
32x=1710
x=1710:32
x=1715
Vậy x∈{−1315;1715}.
c) |x + 1| = 4,5
- Trường hợp 1: x + 1 = 4,5
x = 4,5 − 1
x = 3,5.
- Trường hợp 1: x + 1 = −4,5
x = −4,5 − 1
x = −5,5.
Vậy x ∈{3,5; −5,5}.
Bài 3 (1,5 điểm):
Gọi số học sinh giỏi, khá, trung bình của lớp 7A lần lượt là a, b, c (học sinh) (a, b, c ∈ℕ*; a, b, c < 48), ta có:
Số học sinh giỏi, khá, trung bình lần lượt tỉ lệ với 4; 5; 3 nên:
a4=b5=c3.
Theo đề bài, lớp 7A có 48 học sinh nên a + b + c = 48.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a4=b5=c3=a+b+c4+5+3=4812=4.
Suy ra: a = 4 . 4 = 16;
b = 4 . 5 = 20;
c = 4 . 3 = 12.
Vậy số học sinh giỏi, khá, trung bình của lớp 7A lần lượt là 16 học sinh, 20 học sinh và 12 học sinh.
Bài 4 (2,5 điểm):
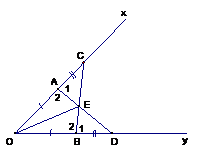
|
GT |
^xOy < 90o; A, C Î Ox: OA < OC; AD ∩ BC=E |
|
KL |
a) AD = BC. b) ∆ EAC = ∆EBD. c) OE là tia phân giác của ^xOy. |
a) Chứng minh: AD = BC.
Xét ∆OAD và ∆OBC có:
OA = OB (gt);
^AOD chung;
OD = OC (gt)
Do đó ∆OAD = ∆OBC (c.g.c)
Suy ra AD = BC (hai cạnh tương ứng)
b) Chứng minh: ∆EAC = ∆EBD.
Vì ∆OAD = ∆OBC (câu a)
Nên ˆA2=ˆB2 (hai góc tương ứng)
Mà ˆA1+ˆA2=180o, ˆB1+ˆB2=180o (kề bù)
Do đó ˆA1=ˆB1.
Mặt khác, OA = OB, OC = OD
Suy ra OC – OA = OD – OB
Do đó AC = BD
Xét ∆EAC và ∆EBD có:
ˆA1=ˆB1 (cmt);
AC = BD (cmt);
^OCB=^ODA (vì ∆OAD = ∆OBC)
Do đó ∆EAC = ∆EBD (g.c.g).
c) Chứng minh: OE là tia phân giác của góc xOy.
Vì ∆EAC = ∆EBD (câu b)
Nên AE = BE (hai cạnh tương ứng).
OA = OB (gt);
Cạnh OE chung;
AE = BE (cmt)
Do đó ∆OAE và ∆OBE (c.c.c)
Suy ra ^AOE=^BOE (hai góc tương ứng)
Hay OE là phân giác của góc xOy.
Bài 5 (0,5 điểm):
1c=12(1a+1b) (với a, b, c ≠ 0, b ≠ c)
⇔1c=a+b2ab
=> 2ab = a(a + b)
=> 2ab = ac + bc
=> ab + ab = ac + bc
=> ab – bc = ac – ab
=> b(a – c) = a(c – b)
⇔ab=a−cc−b
Vậy ab=a−cc−b.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 7
Thời gian làm bài: 45 phút
(Đề số 4)
Bài 1 (1,5 điểm): Thực hiện phép tính (Tính nhanh nếu có thể)
a) −215+310
b) 9 . (−13)2+16 . √4
c) 1514:57−2514:57
Bài 2 (1,5 điểm): Tìm x, biết:
a) x−23=−521
b) x2 + 15 = 20
c) 23x=−521.
Bài 3 (1,5 điểm): Ba đơn vị kinh doanh gốp vốn theo tỉ lệ 3; 5; 7. Hỏi mỗi đơn vị chia bao nhiêu lãi nếu tổng số tiền lãi là 450 triệu đồng và tiền lãi được chia tỉ lệ thuận với số vốn đã góp.
Bài 4 (2 điểm): Cho đồ thị của hàm số y=(m−12)x (với m là hằng số, m≠12) đi qua điểm A (2; 6).
a) Xác định m.
b) Vẽ đồ thị của hàm số đã cho với giá trị m tìm được ở câu a. Tìm trên đồ thị hàm số trên điểm có tung độ bằng 2.
Bài 5 (3 điểm):
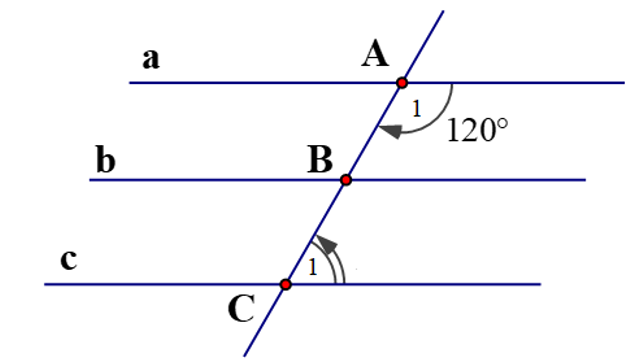
1) Cho hình vẽ sau, biết a // b và b // c. Tính số đo ˆC1?
2) Cho ∆ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA.
a) Chứng minh: ∆ABD = ∆HBD.
b) Chứng minh: DH⊥BC.
c) Giả sử ˆC=60o. Tính số đo ^ADB.
Bài 6 (0,5 điểm): So sánh 230 + 330 + 430 và 3 . 2410.
Đáp án
Bài 1 (1,5 điểm):
a) −215+310
=−430+930
=530=16.
b) 9 . (−13)2+16 . √4
=9 . 19 +16 . 2
=1 +13
=43 .
c) 1514:57−2514:57
=(1514−2514) : 57
=−10 . 75 = −14.
Bài 2 (1,5 điểm):
a) x−23=−521
x=23−521
x=1421−521
x=37.
Vậy x=37.
b) x2 + 15 = 20
x2 = 20 − 15
x2 = 5
x=√5 hoặc x=−√5
Vậy x∈{√5; −√5}.
c) 23x=−521
x=−521:23
x=−521 . 32
x=−514
Vậy x=−514.
Bài 3 (1,5 điểm):
Gọi a, b, c lần lượt là số tiền lãi của ba đơn vị kinh doanh nhận được (triệu đồng) (0 < a, b, c < 450).
Ta có số tiền lãi tỉ lệ thuận với số vốn đã góp.
Giả sử a, b, c lần lượt tỉ lệ với 3; 5; 7 nên a3=b5=c7.
Tổng số tiền lãi là 450 triệu đồng nên a + b + c = 450.
Áp dụng tính chất dãy tỉ số bằng nhau:
a3=b5=c7=a+b+c3+5+7=45015=30
Do đó: a = 3. 30;
b = 5 . 30 = 150;
c = 7 . 30 = 210.
Vậy số tiền lãi của ba đơn vị nhận được lần lượt là: 90 triệu đồng; 150 triệu đồng và 210 triệu đồng.
Bài 4 (2 điểm):
a) Hàm số y=(m−12)x (với m là hằng số, m≠12) đi qua điểm A (2; 6).
Nên: 6=(m−12) . 2
m−12=3
m=72.
Vậy m=72.
b) Với m=72, ta có đồ thị hàm số y = 3x.
* Cách vẽ:
- Vẽ hệ trục tọa độ Oxy.
- Đồ thị hàm số đi qua O (0; 0).
- Với x = 1 ta được y = 1. 3 = 3, điểm A (1; 3) thuộc đồ thị hàm số y = 3x.
Do đó, đường thẳng OA là đồ thị của hàm số đã cho.
* Ta có đồ thị hàm số y = 3x.
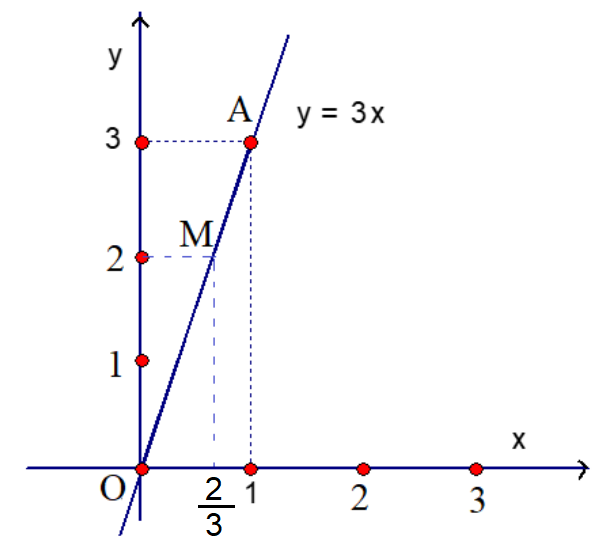
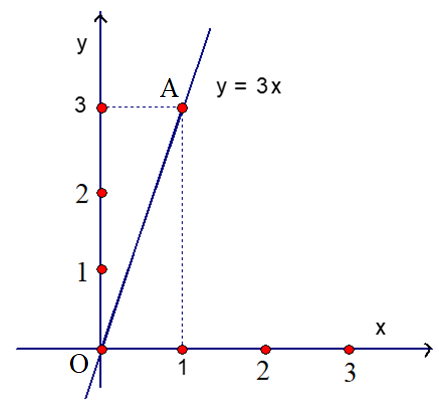 Điểm có tung độ bằng 2 hay y = 2. Khi đó, x=y3=23.
Điểm có tung độ bằng 2 hay y = 2. Khi đó, x=y3=23.
Do đó, điểm M(23; 2) thuộc đồ thị hàm số y = 3x và có tung độ bằng 2 (như hình vẽ).
Bài 5 (3 điểm):
1)
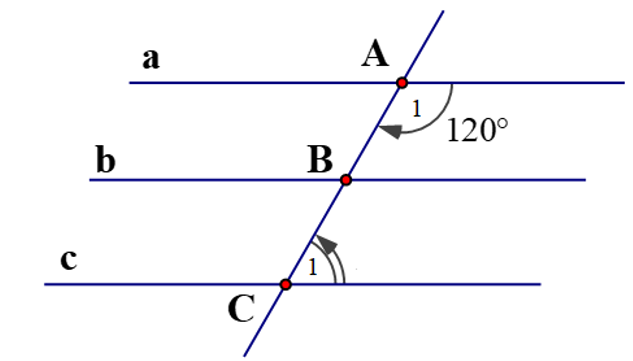 Ta có: a // b và b // c.
Ta có: a // b và b // c.
Suy ra: a // c (tính chất ba đường thẳng song song).
Ta lại có: ˆA1 và ˆC1 là hai góc trong cùng phía nên ˆA1+ˆC1=180o.
⇒ˆC1=180o−ˆA1=180o−120o=60o.
Vậy ˆC1=60o.
2)
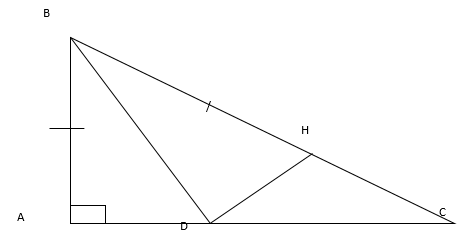
|
GT |
∆ABC vuông tại A BD là tia phân giác ^BAC (D ∈ AC) BH = BA (H ∈ BC), ˆC=60o |
|
KL |
a) ∆ABD = ∆HBD b) DH⊥BC c) ^ADB=? |
Xét ∆ABD và ∆HBD có:
AB = BH (gt)
^ABH=^DBH (vì BD là tia phân giác của ^BAC)
Cạnh BD chung.
Do đó ∆ABD = ∆HBD (c.g.c)
b) Chứng minh: DH⊥BC
Vì ∆ABD = ∆HBD (câu a) nên ^BAD=^BHD (hai góc tương ứng)
Mà ^BAD=90o. Do đó ^BHD= 90o.
Vậy DH ⊥BC.
c) Tính số đo ^ADB.
Ta có ∆ABC vuông tại A nên ^ABC+ˆC=90o.
Mà ˆC=60o nên ^ABC=30o.
Vì BD là tia phân giác của ^BAC.
Nên ^ABD=^DBH=^ABD:2=30o:2=15o.
Ta có ∆ABD vuông tại A nên ^ABD+^ADB=90o.
^ADB=90o−^ABD=90o−15o=75o
Vậy ^ADB=75o.
Bài 6 (0,5 điểm):
Ta có: 430 = (2 . 2)30 = 230 . 230 = (23)10 . (22)15 = 810 . 415
Lại có: 2410 . 3 = (8 . 3)10 . 3 = 810 . 310. 3 = 810 . 311
Ta thấy 415 > 411 > 311
Suy ra 810 . 415 > 810 . 311
Hay 430 > 3 . 2410
Do đó 230 + 330 + 430 > 3 . 2410.
Vậy 230 + 330 + 430 > 3 . 2410.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 7
Thời gian làm bài: 45 phút
(Đề số 5)
Bài 1 (1,5 điểm): Thực hiện các phép tính (tính hợp lý nếu có thể)
a) 23⋅(34−57)−128:(−56+13)
b) 1237+321+2537−714+67
Bài 2 (1,5 điểm): Tìm x, biết:
a) 132−x=53
b) x:43=214:13
c) |x−12|−√25=−2
Bài 3 (1,5 điểm): Tìm a, b, c biết:
a) a2=b3=c4 và a + b + c = 81.
b) Cho 2a = 3b; 4b = 5c và 2a + 3b – 4c = 56.
Bài 4 (2 điểm):
a) Tìm chiều rộng và chiều dài của hình chữ nhật, biết chúng tỉ lệ với 3; 4 và hình chữ nhật có chu vi là 56 mét.
b) Một ô tô chạy từ A đến B với vận tốc 45km/h mất 3giờ. Hỏi ô tô chạy từ A đến B với vận tốc 65km/h mất bao nhiêu giờ? (kết quả làm tròn đến chữ số thập phân thứ nhất).
Bài 5 (3 điểm):
1) Cho hình vẽ. Tính số đo của ^ACB trong hình vẽ bên dưới.
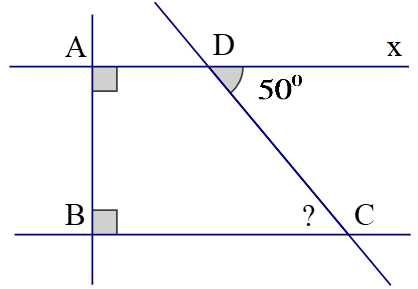 2) Cho tam giác ABC vuông tại A có ˆB=60o. Vẽ AH⊥BC tại H.
2) Cho tam giác ABC vuông tại A có ˆB=60o. Vẽ AH⊥BC tại H.
a) Tính số đo góc HAB.
b) Trên cạnh AC lấy điểm D sao cho AD = AH. Gọi I là trung điểm của cạnh HD. Chứng minh ∆AHI = ∆ADI. Từ đó suy ra AI ⊥ HD.
c) Tia AI cắt cạnh HC tại điểm K. Chứng minh AB // KD.
Bài 6 (0,5 điểm): Tìm x biết: |3x −1| + |1 – 3x| = 6
Đáp án
Bài 1 (1,5 điểm):
a) 23⋅(34−57)−128:(−56+13)
=23⋅(2128−2028)−128:(−56+26)
=23⋅128−128:(−36)
=23⋅128+128⋅2
=128⋅(23+2)
=128⋅83=221.
b) 1237+321+2537−714+67
=(1237+2537)+(321+67)−714
=3737+(321+1821)−12
=1+1−12
=2−12=32.
Bài 2 (1,5 điểm):
a) 132−x=53
52−x=53
x=52−53
x=56
Vậy x=56.
b) x:43=214:13
x:43=94 . 3
x:43=274
x=274 . 43
x = 9.
Vậy x = 9.
c) |x−12|−√25=−2
|x−12|−5=−2
|x−12|=3
- Trường hợp 1: x−12=3
x=3+12
x=72.
- Trường hợp 2: x−12=3
x=−3+12
x=−52
Vậy x∈{72; −52}.
Bài 3 (1,5 điểm):
a) a2=b3=c4 và a + b + c = 81.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
a2=b3=c4=a+b+c2+3+4=819=9
Do đó a = 9 . 2 = 18;
b = 9 . 3 = 27;
c = 9 . 4 = 36.
Vậy a = 18, b = 27, c = 36.
b) Cho 2a = 3b; 4b = 5c và 2a + 3b – 4c = 56.
Ta có 2a = 3b; 4b = 5c nên a3=b2; b5=c4
⇒a15=b10; b10=c8
⇒a15=b10=c8
⇒2a30=3b30=4c32.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
2a30=3b30=4c32=2a+3b+4c30+30+32=5628=2.
Do đó, 2a = 30 . 2 = 60 => a = 30;
3b = 30 . 2 = 60 => b = 20;
4c = 32 . 2 = 64 => c = 16.
Vậy a = 30; b = 20; c = 16.
Bài 4 (2 điểm):
a) Gọi x, y lần lượt là chiều rộng và chiều dài hình chữ nhật (m) (y > x > 0).
Vì chiều rộng và chiều dài của hình chữ nhật tỉ lệ với 3 và 4 nên x3=y4;
Chu vi của hình chữ nhật là 56 mét nên 2(x + y) = 56.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
x3=y4=x+y3+4=287=4.
Do đó x = 3 . 4 = 12;
y = 4 . 4 = 16.
Vậy hình chữ nhật có chiều rộng là 12m và chiều dài là 16m.
b) Gọi x (giờ) là thời gian để ô tô chạy từ A đến B với vận tốc 65km/h.
Điều kiện: x > 0.
Hai ô tô cùng chạy trên một quãng đường AB nên vận tốc và thời gian của ô tô là hai đại lượng tỉ lệ nghịch.
Suy ra: x3=4565.
Do đó x=3 . 4565=2713≈2,1.
Vậy ô tô chạy từ A đến B với vận tốc 65km/h mất khoảng 2,1 giờ.
Bài 5 (3 điểm):
1)
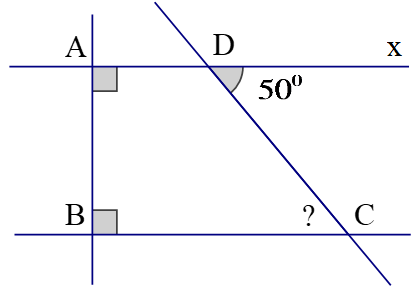 Dựa vào hình vẽ, ta có: AD⊥AB và AB⊥BC.
Dựa vào hình vẽ, ta có: AD⊥AB và AB⊥BC.
Nên AD // BC (quan hệ giữa tính vuông góc với tính song song).
Vì AD // BC mà ^CDx và ^ACB là hai góc so le trong.
Nên ^ACB = ^CDx = 50o.
Vậy ^ACB = 50o.
2) Cho tam giác ABC vuông tại A có ˆB=60o. Vẽ AH⊥BC tại H.
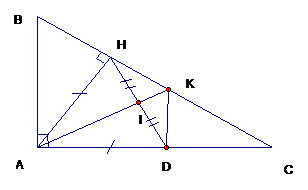
|
GT |
∆ABC vuông tại A, ˆB=60o; AH AD = AH (D ∈AC); I là trung điểm của HD AI∩HC=K. |
|
KL |
a) ^HAB=? b) ∆AHI = ∆ADI; AI ⊥ HD. c) AB // KD |
a) Tính số đo góc HAB.
Xét ∆AHB vuông tại H có:
^HBA+^HAB=90o (hai góc phụ nhau)
⇒^HAB=90o−^HBA=90o−60o=30o
Vậy .
b) Chứng minh ∆AHI = ∆ADI. Từ đó suy ra AI HD.
Xét DAHI và DADI có:
AH = AD (gt)
IH = ID (gt)
AI cạnh chung
Do đó DAHI = DADI (c.c.c)
Suy ra (hai góc tương ứng)
Mà (hai góc kề bù)
Nên
Do đó (đpcm).
c) Chứng minh AB // KD.
DAHI = DADI (cmt)
(hai góc tương ứng).
Xét DAHK và DADK có:
AH = AD (cmt)
(cmt)
Cạnh AK chung.
Do đó (c.g.c)
(hai góc tương ứng)
.
Mà (gt).
Do đó KD //AB (đpcm).
Bài 6 (0,5 điểm):
Vì 3x – 1 và 1 – 3x là hai số đối nhau, nên: |3x −1| = |1 – 3x|
Suy ra: 2 |3x −1| = 6 hoặc |3x −1| = 3
- Trường hợp 1: 3x −1 = 3
3x = 3 + 1
3x = 4
.
- Trường hợp 2: 3x −1 = −3
3x = −3 + 1
3x = −2
.
Vậy .
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 7
Thời gian làm bài: 45 phút
(Đề số 6)
Bài 1 (1,5 điểm): Thực hiện các phép tính (bằng cách hợp lý nếu có):
a)
b)
c)
Bài 2 (1,5 điểm): Tìm x biết:
a)
b)
c)
Bài 3 (2 điểm):
a) Tìm số học sinh của lớp 7A và lớp 7B, biết số học sinh của lớp 7B ít hơn 7A là 6 học sinh và tỉ số học sinh của lớp 7A và 7B là 7 : 6?
b) Cho biết 3 máy cày, cày xong một cánh đồng hết 30 giờ. Hỏi 5 máy cày (cùng năng suất) như thế cày xong cánh đồng đó hết bao nhiêu giờ?
Bài 4 (1,5 điểm): Cho hàm số y = −3x.
a) Vẽ đồ thị của hàm số.
b) Tính giá trị của x (làm tròn đến chữ số thập phân thứ hai) khi y = 2.
Bài 5 (3 điểm):
1) Cho hình vẽ có .
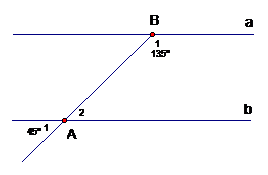 a) Tính số đo góc A2?
a) Tính số đo góc A2?
b) Chứng minh a // b.
2) Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.
a) Chứng minh ∆ABH = ∆ACH.
b) Chứng minh
c) Vẽ và . Chứng minh: DE // BC.
Bài 6 (0,5 điểm): Chứng minh rằng nếu thì:
(với b, c ≠ 0).
Đáp án
Bài 1 (1,5 điểm):
a)
.
b)
.
c)
.
Bài 2 (1,5 điểm):
a)
x + 1,5 = 5,6
x = 5,6 − 1,5
x = 4,1
Vậy x = 4,1.
b)
Vậy .
c)
- Trường hợp 1:
.
- Trường hợp 2:
.
Vậy .
Bài 3 (2 điểm):
a) Gọi x, y lần lượt là số học sinh lớp 7A và lớp 7B (học sinh) (x, y .
Tỉ số học sinh của lớp 7A và 7B là 7 : 6 nên .
Vì số học sinh của lớp 7B ít hơn 7A là 6 học sinh nên x – y = 6.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Do đó: x = 7 . 6 = 42; y = 6 . 6 = 36.
Vậy lớp 7A có 42 học sinh và lớp 7B có 36 học sinh.
b) Gọi x (giờ) là thời gian để 5 máy cày (cùng năng suất), cày xong cánh đồng (x > 0).
Làm việc trên cùng một cánh đồng nên số máy cày (cùng năng suất) và thời gian cày xong cánh đồng là hai đại lượng tỉ lệ nghịch.
Suy ra: .
Do đó .
Vậy 5 máy cày (cùng năng suất) thì cày xong cánh đồng hết 18 giờ.
Bài 4 (1,5 điểm):
a) Vẽ đồ thị của hàm số y = −3x.
- Vẽ hệ trục tọa độ Oxy;
- Với x = 1 thì y = −3, ta được điểm A (1; −3) thuộc đồ thị hàm số y = −3x.
Do đó đường thẳng OA là đồ thị hàm số đã cho.
b) Thay y = 2 vào hàm số y = −3x, ta được:
−3x = 2
.
Vậy khi y = 2 thì x ≈ −0,67.
Bài 5 (3 điểm):
1)
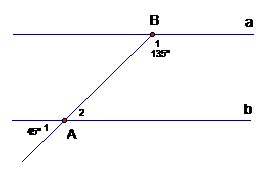
a) Vì và là hai góc đối đỉnh nên .
Vậy .
b) Chứng minh a // b.
Ta có:
Mà và là cặp góc trong cùng phía.
Do đó a // b (đpcm).
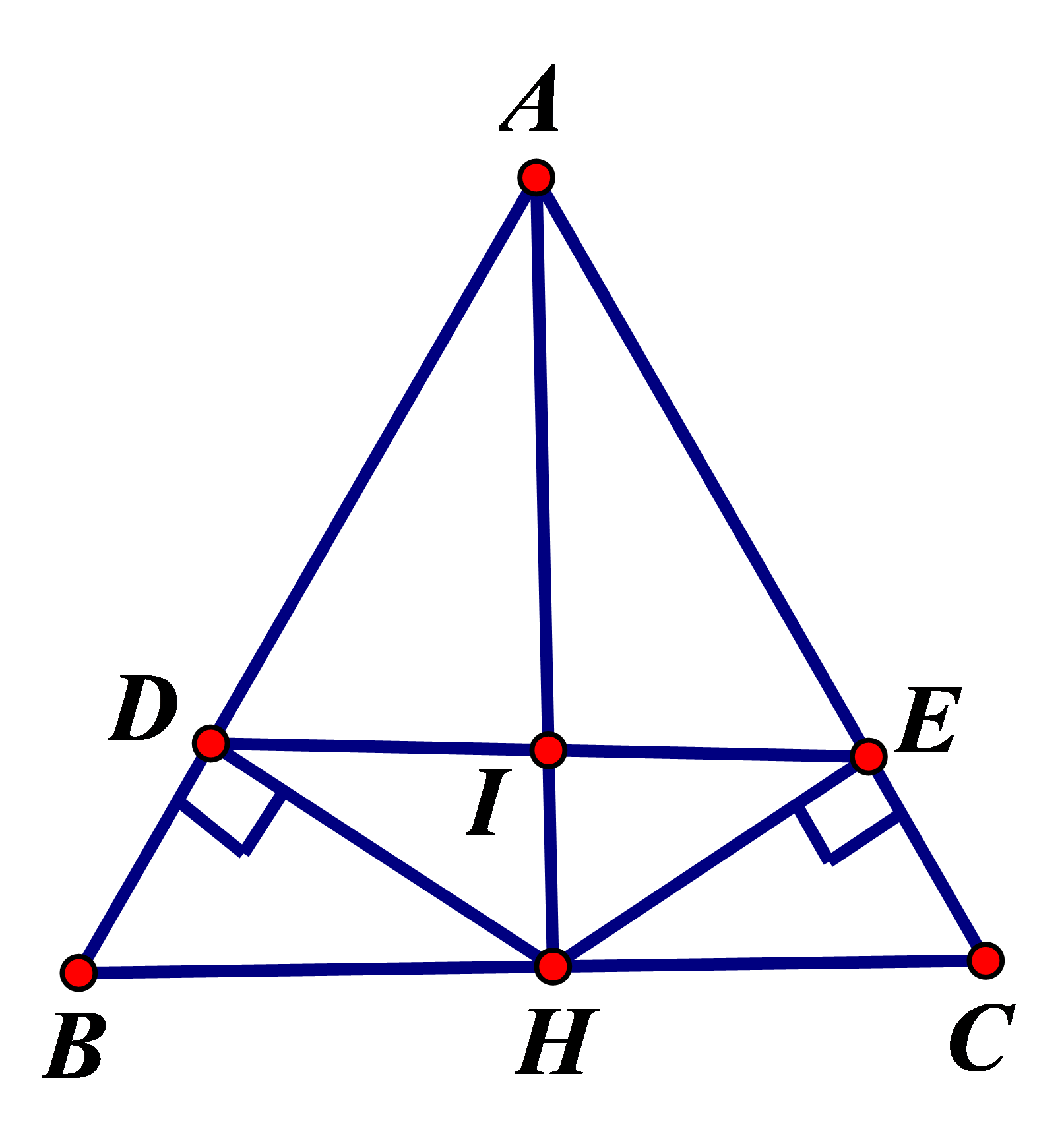
2)
|
GT |
∆ABC: AB = AC; AH là tia phân giác (); AHBC tại H; và . |
|
KL |
a) ∆ABH = ∆ACH b) c) DE // BC |
a) Chứng minh ∆ABH = ∆ACH
Xét ∆ABH và ∆ACH có:
AB = AC (gt)
(gt)
AH cạnh chung
Do đó ∆ABH = ∆ACH (c.g.c)
b) Chứng minh
Vì ∆ABH = ∆ACH (câu a) nên
Mà = 180o (hai góc kề bù)
Suy ra: = 90o.
Vậy AH ![]() BC.
BC.
c) Chứng minh: DE // BC.
Gọi I là giao điểm của AH và DE.
Xét ∆ADH vuông tại D và ∆AEH vuông tại E có:
(gt)
Cạnh AH chung
Do đó ∆ADH = ∆AEH (cạnh huyền – góc nhọn)
Suy ra AD = AE (hai cạnh tương ứng)
Xét ∆ADI và ∆AEI có:
AD = AE (cmt)
(vì AH là tia phân giác )
Cạnh AI chung
Do đó ∆ADI = ∆AEI (c.g.c)
Suy ra (hai góc tương ứng)
Mà = 180o (hai góc kề bù)
Suy ra: = 90o hay AH DE
Ta có: AH BC và AH DE (cmt)
Do đó DE // BC (quan hệ tính vuông góc với tính song song).
Bài 6 (0,5 điểm):
Ta có: (Tính chất tỉ lệ thức)
Lại có: (Tính chất dãy tỉ số bằng nhau)
Do đó:
Vậy .
Xem thêm các chương trình khác:
