Hệ thống kiến thức Toán lớp 7 Học kì 1
Hệ thống kiến thức Toán lớp 7 Học kì 1 giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 7 Giữa học kì 1. Mời các bạn cùng đón xem:
Hệ thống kiến thức Toán lớp 7 Học kì 1
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 7
Thời gian làm bài: 45 phút
(Đề số 1)
I. TRẮC NGHIỆM (3,0 điểm)
Hãy chọn phương án trả lời đúng.
Câu 1: Kết quả phép tính là:
A. 1
B. 3
C. -5
D. 5
Câu 2: Cho hàm số y = , khi đó hệ số tỉ lệ k là:
A. 1
B. 3
C.
D. 4
Câu 3: Cho hình vẽ, ta có:
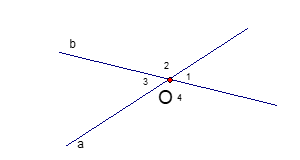
A.
B.
C.
D.
Câu 4: Cho hình vẽ, ta có:
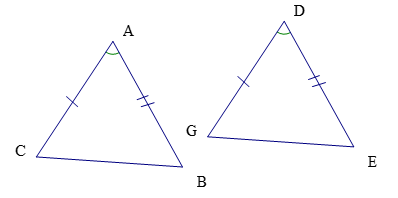
A. (c.g.c)
B. (c.g.c)
C. (c.g.c)
D. (c.g.c)
Câu 5. Kết quả của phép tính là :
A.
B.
C.
D.
Câu 6. Cho hàm số y = |2x - 1|, giá trị của hàm số tại x = -1 là:
A. 1
B. -3
C. 3
D. -1
II. TỰ LUẬN (7,0 điểm)
Câu 1: (1,0 điểm) Thực hiện các phép tính sau:
a)
b ) 2,9 + + (- 4,2) + (-2,9) + 4,2
Câu 2: (1,0 điểm)
Ba đội máy san đất cùng làm một khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 6 ngày, đội thứ hai trong 10 ngày và đội thứ ba trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy (các máy có cùng năng suất), biết đội thứ hai có ít hơn đội thứ ba 3 máy.
Câu 3: (1,0 điểm)
Cho hàm số y = f(x) = ax ( a 0)
a) Tìm a biết đồ thị hàm số đi qua điểm A(1; 3)
b) Vẽ đồ thị ứng với giá trị a vừa tìm được.
Câu 4: (1,5 điểm)
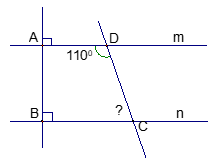 Cho hình vẽ:
Cho hình vẽ:
a) Vì sao m // n ?
b) Tính số đo góc BCD.
Câu 5: (2 điểm)
Cho tam giác ABC vuông ở A. Biết = 500. Lấy điểm M là trung điểm AC. Trên tia đối của tia MB lấy điểm E sao cho MB = ME.
a) Tính số đo góc ACB.
b) Chứng minh AMB = CME.
Câu 6: (0,5 điểm)
Cho B = . Tìm x Z để B có giá trị nguyên.
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. TRẮC NGHIỆM (3 điểm)
Mỗi câu đúng được 0,5 điểm
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
|
Đáp án |
A |
C |
B |
D |
A |
C |
Câu 1:
Ta có: =
Chọn đáp án A
Câu 2:
Hàm số là y = x, nên hệ số tỉ lệ là k =
Chọn đáp án C
Câu 3:
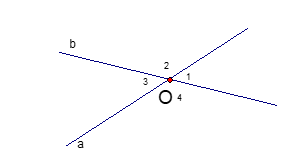
Theo hình vẽ ta có: ; (các góc đối đỉnh)
Chọn đáp án B
Câu 4:
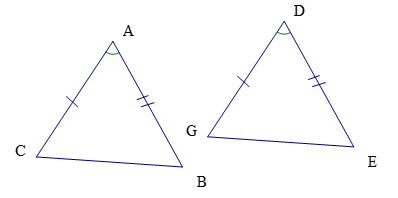 Xét tam giác ABC và tam giác DGE có:
Xét tam giác ABC và tam giác DGE có:
AC = DG; AB = DE;
Do đó: (c.g.c)
Chọn đáp án D
Câu 5:
Ta có: =
Chọn đáp án A
Câu 6:
Thay x = -1 vào hàm số ta được:
y = |2.(-1) - 1| = |-3| = 3
Chọn đáp án C
II. TỰ LUẬN
Câu 1.
a)
= (0,25 điểm)
= (0,25 điểm)
b) 2,9 + + (- 4,2) + (-2,9) + 4,2
= [2,9 + (-2,9)] + [(-4,2) + 4,2] + (0,25 điểm)
= 0 + 0 + 5
= 5 (0,25 điểm)
Câu 2.
Gọi số máy của 3 độ lần lượt là x; y; z ( x; y; z )
Theo đề ra ta có: z - y = 3 (0,25 điểm)
Vì số máy và thời gian làm việc là hai đại lượng tỉ lệ nghịch nên:
6x = 10y = 8z => (0,25 điểm)
Theo tính chất của dãy tỉ số bằng nhau ta có:
= (0,25 điểm)
Do đó: x = 120. = 20
y = 120. = 12
z = 120. = 15
Vậy số máy của 3 đội lần lượt là: 20; 12; 15 máy. (0,25 điểm)
Câu 3.
a) Vì đồ thị hàm số y = ax đi qua điểm A(1; 3) nên:
3 = a.1 a = 3 : 1 = 3
Vậy hàm số là y = 3x với hệ số a = 3. (0,5 điểm)
b) Đồ thị hàm số y = 3x đi qua A(1; 3) và O(0; 0).
Vẽ đường thẳng đi qua A(1; 3) và O(0; 0) ta được đồ thị của hàm số y = 3x.
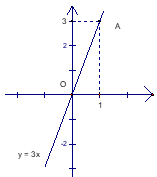 Vậy đồ thị hàm số y = 3x là đường thẳng OA. (0,5 điểm)
Vậy đồ thị hàm số y = 3x là đường thẳng OA. (0,5 điểm)
Câu 4.
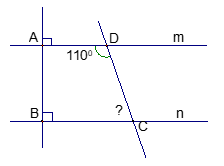
a) Theo hình vẽ ta có: m AB và n AB
Do đó: m // n (0,75 điểm)
b) Vì m // n => = 1800 (2 góc trong cùng phía) (0,25 điểm)
=> = 1800 - (0,25 điểm)
=> = 1800 - 1100 = 700 (0,25 điểm)
Câu 5.
 (0,25 điểm)
(0,25 điểm)
|
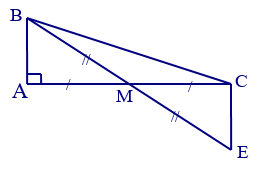
GT |
∆ABC vuông ở A. = 500 M AC; AM = MC; MB = ME (MB và ME là hai tia đối) |
|
KL |
a) Góc ACB = ? b) AMB = CME |
(0,25 điểm)
Chứng minh
a) Áp dụng định lý tổng 3 góc trong tam giác ABC ta có:
+ + = 1800
=> = 1800- ( + )
=> = 1800- (500 + 900) = 400 (0,5 điểm)
b) Xét AMB và CME có:
AM = CM (M là trung điểm của AC)
(2 góc đối đỉnh)
MB = ME (gt)
Do đó: AMB = CME (c.g.c) (1 điểm)
Câu 6.
Để B có nghĩa thì x 0 và x # 1
B = giá trị nguyên khi ( - 1) là ước của 5.
=> ( - 1) (0,25 điểm)
TH1: ( - 1) = -5 => = -4 (loại)
TH2: ( - 1) = -1 => = 0 => x = 0
TH3: ( - 1) = 1 => = 2 => x = 4
TH4: ( - 1) = 5 => = 6 => x = 36
Vậy x {0; 4; 36} thì B đạt giá trị nguyên. (0,25 điểm)
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 7
Thời gian làm bài: 45 phút
(Đề số 2)
I. TRẮC NGHIỆM (2 điểm):
Hãy chọn câu trả lời đúng nhất.
Câu 1: Trong các phân số sau, phân số nào biểu diễn số hữu tỷ ?
A.
B.
C.
D.
Câu 2: Số là kết quả của phép tính:
A.
B.
C.
D.
Câu 3: Cho x và y là hai đại lượng tỉ lệ thuận và x = 6 thì y = 4. Hệ số tỉ lệ k của y đối với x là:
A. k = 24 B. k = C. k = D. k =
Câu 4: Căn bậc hai của 9 bằng:
A. 3
B. -3
C. 3 và -3
D. 81
Câu 5: Cách viết nào dưới đây là đúng?
A.
B.
C.
D.
Câu 6: Kết quả của phép tính (-5)2. (-5)3 là:
A.
B.
C.
D.
Câu 7: Tam giác ABC có và . Góc B bằng:
A.
B.
C.
D.
Câu 8: Hai đường thẳng song song là hai đường thẳng:
A. Có ít nhất hai điểm chung.
B. Không có điểm chung.
C. Không vuông góc với nhau.
D. Chỉ có một điểm chung.
II. TỰ LUẬN (8 điểm)
Bài 1 (1,5 điểm): Thực hiện phép tính.
a)
b)
Bài 2 (1,5 điểm): Cho hàm số y = f(x) = (m + 1)x
Tìm m để f(2) = 4. Vẽ đồ thị hàm số với m tìm được.
Bài 3 (1,5 điểm): Tìm x, y, z biết:
a)
b) và x + 2y - z = 14
Bài 4 (3 điểm): Cho tam giác ABC. Gọi M là trung điểm của BC. Trên tia đối của MA lấy điểm K sao cho MK = MA.
a) Chứng minh và CK song song AB.
b) Biết . Tính .
Bài 5(0,5đ): Cho tam giác ABC. Tia phân giác của góc B cắt AC tại M. Tia phân giác của góc C cắt AB tại N. Giả sử BN + CM = BC. Hãy tính số đó góc A.
ĐÁP ÁN VÀ BIỂU ĐIỂM
I.PHẦN TRẮC NGHIỆM (2,0 điểm) Mỗi câu đúng được 0,25 điểm
|
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
|
C |
A |
D |
C |
B |
A |
D |
B |
Câu 1.
Ta có: ; ; ;
Chọn đáp án C
Câu 2.
Ta có:
Chọn đáp án A
Câu 3.
Vì x và y là hai đại lượng tỉ lệ thuận nên ta có y = kx
Với x = 6 thì y = 4 nên thay vào ta được: 4 = k.6 => k =
Chọn đáp án D
Câu 4.
9 có hai căn bậc hai là và
Chọn đáp án C
Câu 5.
Ta có: |-0,55| = 0,55 ; -|-0,55| = -0,55; -|0,55| = -0,55
Chọn đáp án B
Câu 6.
Ta có: (-5)2 . (-5)3 = (-5)2+3 = (-5)5
Chọn đáp án A
Câu 7.
Theo định lý tổng ba góc trong tam giác ABC ta có:
Mà
Nên
Chọn đáp án D
Câu 8.
Hai đường thẳng song song là hai đường thẳng không có điểm chung (định nghĩa hai đường thẳng song song).
Chọn đáp án B
II. PHẦN TỰ LUẬN (8 điểm)
Bài 1.
a)
(0,25 điểm)
(0,25 điểm)
(0,25 điểm)
b) (0,5 điểm)
(0,25 điểm)
Bài 2.
a) Ta có f(2) = 4
Thay x = 2 vào hàm số ta được: (m + 1).2 = 4
m + 1 = 2 m = 1
Vậy m = 1 thì f(2) = 4. (0,75 điểm)
b) Với m =1 thì ta có hàm số: y = f(x) = 2x
Lấy x = 1 thì y = 2.1 = 2 nên điểm A(1; 2) thuộc đồ thị hàm số y = 2x
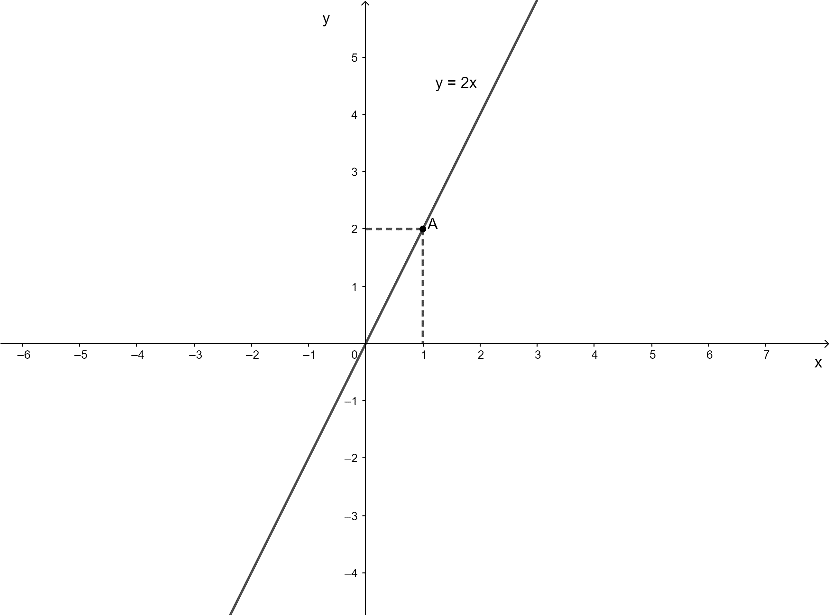
Vậy đồ thị hàm số y = 2x là đường thẳng OA. (0,75 điểm)
Bài 3.
a)
TH1: (0,25 điểm)
TH2: (0,25 điểm)
Vậy hoặc . (0,25 điểm)
b) và x + 2y - z = 14
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
(vì x + 2y – z =14) (0,25 điểm)
Do đó: (0,25 điểm)
Vậy x =10 ; y = 6 ; z = 8 (0,25 điểm)
Bài 4.
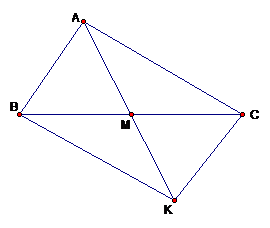
|
GT |
, MB = MC MA = MK (K thuộc tia đối của tia MA)
|
|
KL |
a) CK // AB b) = ? |
(0,5 điểm)
Chứng minh
a) Xét tam giác AMC và KMB có:
AM = MK (gt)
MB = MC (M là trung điểm của BC)
(hai góc đối đỉnh)
Do đó: (c.g.c) (0,75 điểm)
Chứng minh tương tự ta cũng có: (c.g.c) (0,5 điểm)
Suy ra:
Mà hai góc này ở vị trí so le trong
Nên CK // AB (0,5 điểm)
b) Chứng minh được (c.c.c) => (0,25 điểm)
Xét có hay
Mà
Nên => (0,5 điểm)
Bài 5.
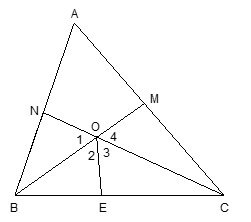 Gọi BM giao CN là O. Trên cạnh BC lấy điểm E sao cho BN = BE mà BN + CM = BC (gt) => CE = CM.
Gọi BM giao CN là O. Trên cạnh BC lấy điểm E sao cho BN = BE mà BN + CM = BC (gt) => CE = CM.
Ta chứng minh (c.g.c) . Chứng minh tương tự . Mà (hai góc đối đỉnh) => (0,25 điểm)
Ta có: => =>
Ta có . Mà
=> => (0,25 điểm)
Xem thêm các chương trình khác:
