Sách bài tập Toán 9 (Cánh diều): Bài tập cuối chương 4

Giải SBT Toán 9 Bài tập cuối chương 4 - Cánh diều

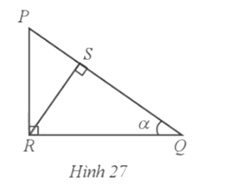
Bài 27 trang 90 SBT Toán 9 Tập 1: Cho tam giác PQR vuông tại R có đường cao RS và $\widehat{Q}=\alpha$ (Hình 27). Tỉ số lượng giác sin α bằng:

Lời giải:

Đáp án đúng là: D

Xét ∆RSQ vuông tại S có $\sin \widehat{RQS}=\frac{RS}{QR}$ hay $\sin \alpha =\frac{RS}{QR}.$

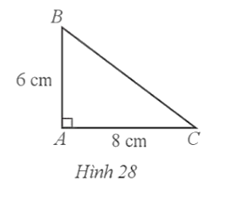
Bài 28 trang 90 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm (Hình 28). Tỉ số lượng giác cot bằng

Lời giải:

Đáp án đúng là: A

Tam giác ABC vuông tại A có: $\cot C=\frac{AC}{AB}=\frac{8}{6}=\frac{4}{3}.$

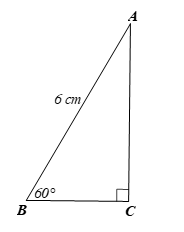
Bài 29 trang 90 SBT Toán 9 Tập 1: Một chiếc thang dài 6 m được đặt dựa vào tường và tạo với phương nằm ngang một góc 60°. Khi đó, khoảng cách giữa chân thang và chân tường là:

Lời giải:

Đáp án đúng là: A

Độ dài chiếc thang là AB = 6 m, chiếc thang tạo với phương nằm ngang một góc 60° nên $\widehat{ABC}=60°.$

Xét ∆ABC vuông tại A có:

$BC=AB\cdot \cos \widehat{ABC}=6\cdot \cos 60°=6\cdot \frac{1}{2}=3\text{ (m).}$

Vậy khoảng cách giữa chân thang và chân tường là 3 m.

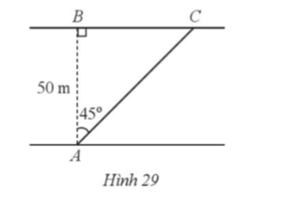
Bài 30 trang 90 SBT Toán 9 Tập 1: Một con sông có bề rộng AB = 50 m. Một chiếc thuyền đi thẳng từ vị trí A bên này bờ sông đến vị trí C bên kia bờ sông với góc tạo bởi phương AC và phương AB là $\widehat{BAC}=45°$ (Hình 29). Hỏi độ dài đoạn thẳng BC là bao nhiêu mét?

Lời giải:

Vì tam giác ABC vuông tại B nên

$BC=AB\cdot \text{tan}\widehat{BAC}=50\cdot \text{tan}45°=50\cdot 1=50\text{ (m).}$

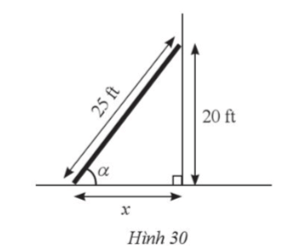
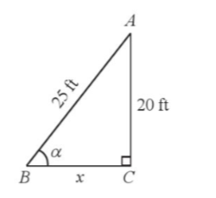
Bài 31 trang 91 SBT Toán 9 Tập 1: Một người lính cứu hoả dựng một chiếc thang dài 25 ft dựa vào tường với góc tạo bởi thang và phương nằm ngang là góc α. Biết đỉnh của chiếc thang cách mặt đất là 20 ft (Hình 30). Tính khoảng cách x từ chân thang đến chân tường và số đo góc α (làm tròn kết quả đến hàng đơn vị của độ).

Lời giải:

Tam giác ABC vuông tại C ở hình vẽ trên mô tả chiếc thang dài AB = 25 ft dựa vào tường với góc tạo bởi thang và phương nằm ngang là góc $\widehat{ABC}=\alpha ,$ đỉnh của chiếc thang cách mặt đất là AC = 20 ft; khoảng cách từ chân thang đến chân tường là BC = x.

Xét ∆ABC vuông tại C, theo định lí Pythagore, ta có:

AB² = AC² + BC²

Suy ra $x=BC=\sqrt{A{B}^2-A{C}^2}=\sqrt{{25}^2-{20}^2}=\sqrt{225}=15\left(\text{ft}\right).$

Do đó $\text{sin}\alpha =\text{sin}\widehat{ABC}=\frac{AC}{AB}=\frac{20}{25}=\frac{4}{5},$ nên α ≈ 53°.

Bài 32 trang 91 SBT Toán 9 Tập 1: Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giá trị mỗi biểu thức sau:

a) sin² 25° + sin² 35° + sin² 55° + sin² 65°;

b) cot 20°.cot 40°.cot 50°.cot 70°.

Lời giải:

Do 25° + 65° = 90°; 35° + 55° = 90° nên

sin² 25° + sin² 35° + sin² 55° + sin² 65°

= (sin² 25° + sin² 65°) + (sin² 35° + sin² 55°)

= (sin² 25° + cos² 25°) + (sin² 35° + cos² 35°)

= 1 + 1 = 2.

b) Do 20° + 70° = 90°; 40° + 50° = 90° nên

cot 20°.cot 40°.cot 50°.cot 70°

= (cot 20°. cot 70°).(cot 40°.cot 50°)

= (tan 70°. cot 70°).(tan 50°.cot 50°)

= 1.1 = 1.

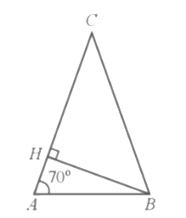
Bài 33 trang 91 SBT Toán 9 Tập 1: Cho tam giác ABC có $\widehat{A}=70°,$ AB = 10 cm, AC = 15 cm. Tính độ dài cạnh BC.

Lời giải:

Kẻ đường cao BH của tam giác ABC.

Vì tam giác ABH vuông tại H nên

⦁ $BH=AB\cdot \sin \widehat{A}=10\cdot \sin 70°\approx 9,397\text{ (cm);}$

⦁ $AH=AB\cdot \cos \widehat{A}=10\cdot \cos 70°\approx 3,42\text{ (cm).}$

Khi đó CH = AC ‒ AH ≈ 15 ‒ 3,42 = 11,58 (cm).

Xét ∆BCH vuông tại H, theo định lí Pythagore, ta có:

BC² = BH² + CH² ≈ 9,397² + 11,58² = 222,400009.

Suy ra $BC\approx \sqrt{222,400009}\approx 15\text{ (cm).}$

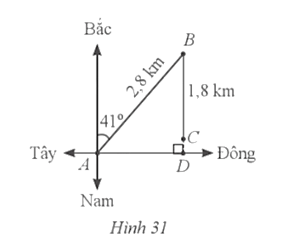
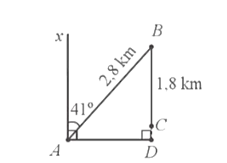
Bài 34 trang 91 SBT Toán 9 Tập 1: Một thuỷ thủ lái thuyền từ bờ (ở vị trí A) ra biển theo hướng Đông Bắc với góc nghiêng so với hướng Bắc là 41°. Đi được 2,8 km thì người đó phát hiện sắp hết nhiên liệu (ở vị trí B), vội quay thuyền vào bờ theo hướng Nam. Người đó đi tiếp được 1,8 km thì thuyền bị tắt máy (ở vị trí C) (Hình 31). Hỏi lúc đó thuyền còn cách bờ bao xa? (làm tròn kết quả đến hàng phần mười của kilômét)?

Lời giải:

Gọi tia Ax là hướng Bắc. Khi đó:

$\widehat{BAx}=41°;$ AB = 2,8 km; BC = 1,8 km.

Ta có: $\widehat{BAx}+\widehat{BAD}=90°$

Suy ra $\widehat{BAD}=90°-\widehat{BAx}=90°-41°=49°.$

Vì tam giác ABD vuông tại D nên

$BD=AB\cdot \sin \widehat{BAD}=2,8\cdot \sin 49°.$

Suy ra CD = BD ‒ BC = 2,8.sin49° ‒ 1,8 ≈ 0,3 (km).

Vậy khoảng cách giữa thuyền và bờ khoảng 0,3 kilômét.

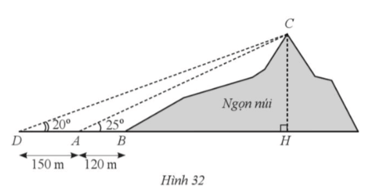
Bài 35 trang 91 SBT Toán 9 Tập 1: Một người (ở vị trí A) đứng cách chân núi (ở vị trí B) là 120 m. Người này đo được góc tạo bởi phương AC và phương nằm ngang là $\widehat{BAC}=25°$ với vị trí C là đỉnh núi. Sau đó, người này di chuyển thêm 150 m ra phía xa ngọn núi hơn đến vị trí D và đo được góc tạo bởi phương DC và phương nằm ngang là $\widehat{BDC}=20°$ (Hình 32). Tính chiều cao CH của ngọn núi (làm tròn kết quả đến hàng đơn vị của mét).

Lời giải:

Vì tam giác ACH vuông tại H nên

$AH=CH\cdot \cot \widehat{CAH}=CH\cdot \cot 25°.$

Vì tam giác DCH vuông tại H nên

$DH=CH\cdot \cot \widehat{CDH}=CH\cdot \cot 20°.$

Do đó, AD = DH ‒ AH = CH.cot20° ‒ CH.cot25° = CH(cot20° ‒ cot25°).

Suy ra $CH=\frac{AD}{\cot 20°-\cot 25°}=\frac{150}{\cot 20°-\cot 25°}\approx 249\text{ (m).}$

Vậy chiều cao của ngọn núi khoảng 249 mét.

Xem thêm Lời giải bài tập Toán 9 sách Cánh diều hay, chi tiết khác:

Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài tập cuối chương 3

Bài 1: Tỉ số lượng giác của góc nhọn

Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 3: Một số hệ thức về cạnh và góc trong tam giác vuông