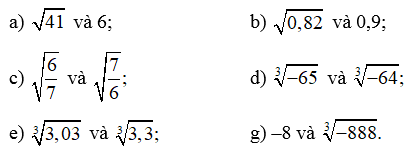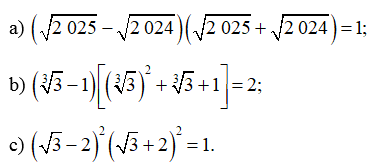Sách bài tập Toán 9 Bài 1 (Cánh diều): Căn bậc hai và căn bậc ba của số thực

Giải SBT Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 1 trang 52 SBT Toán 9 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Căn bậc hai của 25 là 5.

b) Căn bậc hai của 36 là 6 và –6.

c) Căn bậc hai số học của 0,01 là 0,1.

d) Căn bậc hai số học của 7 là $\sqrt{7}.$

Lời giải:

a) Ta có: 5² = 25 và (‒5)² = 25 nên số 5 và ‒5 là căn bậc hai của 25.

Do đó, phát biểu a) là sai.

b) Ta có: 6² = 36 và (‒6)² = 36 nên số 6 và ‒6 là căn bậc hai của 36.

Do đó, phát biểu b) là đúng.

c) Ta có: 0,1² = 0,01 và 0,1 > 0 nên 0,1 là căn bậc hai số học của 0,01.

Do đó, phát biểu c) là đúng.

d) Do ${\left(\sqrt{7}\right)}^2=7$ và $\sqrt{7}>0$ nên $\sqrt{7}$ là căn bậc hai số học của 7.

Do đó, phát biểu d) là đúng.

Bài 2 trang 52 SBT Toán 9 Tập 1: Tìm căn bậc hai của:

a) 144;

b) 2,56;

c) $\frac{169}{81}.$

Lời giải:

a) Do 12² = 144 và (‒12)² = 144 nên căn bậc hai của 144 có hai giá trị là 12 và ‒12.

Cụ thể, ta có: $\sqrt{144}=12$ và $-\sqrt{144}=-12.$

b) Do 1,6² = 2,56 và (‒1,6)² = 2,56 nên căn bậc hai của 2,56 có hai giá trị là 1,6 và ‒1,6.

Cụ thể, ta có: $\sqrt{2,56}=1,6$ và $-\sqrt{2,56}=-1,6.$

c) Do ${\left(\frac{13}{9}\right)}^2=\frac{169}{81}$ và ${\left(-\frac{13}{9}\right)}^2=\frac{169}{81}$ nên căn bậc hai của $\frac{169}{81}$ có hai giá trị là $\frac{13}{9}$ và $-\frac{13}{9}$

Cụ thể, ta có: $\sqrt{\frac{169}{81}}=\frac{13}{9}$và $-\sqrt{\frac{169}{81}}=-\frac{13}{9}.$

Bài 3 trang 52 SBT Toán 9 Tập 1: Tìm căn bậc ba của:

a) 343;

b) –0,512;

c) $\frac{27}{125}$

Lời giải:

a) Ta có: 7³ = 343 nên số 7 là căn bậc ba của 343.

b) Ta có: (‒0,8)³ = –0,512 nên số ‒0,8 là căn bậc ba của ‒0,512.

c) Ta có: ${\left(\frac{3}{5}\right)}^3=\frac{27}{125}$ nên số $\frac{3}{5}$ là căn bậc ba của $\frac{27}{125}$

Bài 4 trang 52 SBT Toán 9 Tập 1: So sánh:

Lời giải:

a) Ta có: $6=\sqrt{36}.$

Mà 41 > 36 nên $\sqrt{41}>\sqrt{36}$ hay $\sqrt{41}>6.$

b) Ta có: $0,9=\sqrt{0,81}.$

Mà 0,82 > 0,81 nên $\sqrt{0,82}>\sqrt{0,81}$ hay $\sqrt{0,82}>0,9.$

c) Ta có: $\frac{6}{7}<\frac{7}{7}=1;$$\frac{7}{6}>\frac{6}{6}=1.$

Do đó $\frac{6}{7}<\frac{7}{6}$ nên $\sqrt{\frac{6}{7}}<\sqrt{\frac{7}{6}}.$

d) Ta có: ‒65 < ‒64 nên $\sqrt[3]{-65}<\sqrt[3]{-64}.$

e) Ta có: 3,03 < 3,3 nên $\sqrt[3]{3,03}<\sqrt[3]{3,3}.$

g) Ta có: (‒8)³ = ‒512; ${\left(\sqrt[3]{-888}\right)}^3=-888.$

Mà ‒512 > ‒888 nên $-8>\sqrt[3]{-888}.$

Bài 5 trang 53 SBT Toán 9 Tập 1: Chứng minh:

Lời giải:

a) Ta có:

$\left(\sqrt{2025}-\sqrt{2024}\right)\left(\sqrt{2025}+\sqrt{2024}\right)$

$={\left(\sqrt{2025}\right)}^2-{\left(\sqrt{2024}\right)}^2=2025-2024=1.$

Vậy $\left(\sqrt{2025}-\sqrt{2024}\right)\left(\sqrt{2025}+\sqrt{2024}\right)=1.$

b) Ta có: $\left(\sqrt[3]{3}-1\right)\left[{\left(\sqrt[3]{3}\right)}^2+\sqrt[3]{3}+1\right]={\left(\sqrt[3]{3}\right)}^3-1^3=3-1=2.$

Vậy $\left(\sqrt[3]{3}-1\right)\left[{\left(\sqrt[3]{3}\right)}^2+\sqrt[3]{3}+1\right]=2.$

c) Ta có:

${\left(\sqrt{3}-2\right)}^2{\left(\sqrt{3}+2\right)}^2={\left[\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)\right]}^2$

$={\left[{\left(\sqrt{3}\right)}^2-2^2\right]}^2={\left(3-4\right)}^2={\left(-1\right)}^2=1.$

Vậy ${\left(\sqrt{3}-2\right)}^2{\left(\sqrt{3}+2\right)}^2=1.$

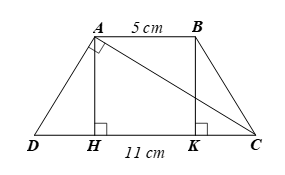
Bài 6 trang 53 SBT Toán 9 Tập 1: Cho hình thang cân ABCD có AB // CD và AC ⊥ AD. Tính độ dài cạnh AD, biết AB = 5 cm và CD = 11 cm.

Lời giải:

Kẻ AH, BK vuông góc với CD lần lượt tại H, K nên AH ⊥ HK, BK ⊥ HK. Do đó AH // BK.

Do AB // CD, mà H, K ∈ CD nên AB // HK.

Xét tứ giác ABKH có AH // BK và AB // HK nên ABKH là hình bình hành.

Lại có $\widehat{AHK}=90°$ nên ABKH là hình chữ nhật.

Suy ra AH = BK và HK = AB = 5 cm.

Xét ∆ADH (vuông tại H) và ∆BCK (vuông tại K) có:

AD = BC (do ABCD là hình thang cân), AH = BK.

Do đó ∆ADH = ∆BCK (cạnh huyền – cạnh góc vuông).

Suy ra DH = CK (hai cạnh tương ứng).

Mà DH + HK + CK = CD

Nên $DH=CK=\frac{CD-HK}{2}=\frac{11-5}{2}=3\text{\hspace{0.17em}\hspace{0.17em}(cm}).$

Xét ∆ACD và ∆HAD có:

$\widehat{DAC}=\widehat{DHA}=90°$ và $\widehat{ACD}$ là góc chung.

Do đó ∆ACD ᔕ ∆HAD (g.g)

Suy ra $\frac{CD}{AD}=\frac{AD}{HD}$ hay AD² = CD.HD.

Vì vậy, $AD=\sqrt{CD\cdot HD}=\sqrt{11\cdot 3}=\sqrt{33} \text{\hspace{0.17em}cm}.$

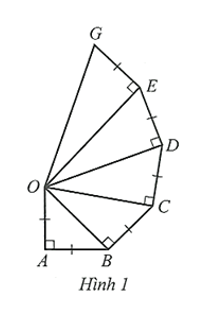
Bài 7 trang 53 SBT Toán 9 Tập 1: Cho Hình 1 có OA = AB = BC = CD = DE = EG = 2 cm và $\widehat{OAB}=\widehat{OBC}=\widehat{OCD}=\widehat{ODE}=\widehat{OEG}=90°.$ Tính độ dài các cạnh OB, OC, OD, OE, OG.

Lời giải:

Áp dụng định lí Pythagore cho tam giác OAB vuông tại A, ta có:

OB² = OA² + AB² = 2² + 2² = 8.

Tương tự, áp dụng định lý Pythagore cho các tam giác vuông OBC, OCD, ODE, OEG ta có:

OC² = OB² + BC² = 8 + 2² = 12;

OD² = OC² + CD² = 12 + 2² = 16;

OE² = OD² + DE² = 16 + 2² = 20;

OG² = OE² + EG² = 20 + 2² = 24.

Suy ra: $OG=\sqrt{24}=2\sqrt{6}\text{\hspace{0.17em}\hspace{0.17em}(cm}).$

Bài 8 trang 53 SBT Toán 9 Tập 1: Trên một đoạn sông, tốc độ dòng chảy của nước ở bề mặt sông lớn hơn tốc độ dòng chảy của nước ở đáy sông. Gọi v (km/h) là tốc độ dòng chảy của nước ở bề mặt sông và f (km/h) là tốc độ dòng chảy của nước ở đáy sông. Khi đó, ta có công thức: $\sqrt{f}=\sqrt{v}-1,3.$

a) Tính tốc độ dòng chảy của nước ở đáy sông, biết tốc độ dòng chảy của nước ở bề mặt sông là 9 km/h.

b) Tính tốc độ dòng chảy của nước ở bề mặt sông, biết tốc độ dòng chảy của nước ở đáy sông là 20,25 km/h.

Lời giải:

a) Thay v = 9 (km/h) vào $\sqrt{f}=\sqrt{v}-1,3,$ ta được:

$\sqrt{f}=\sqrt{9}-1,3=3-1,3=1,7.$

Suy ra f = 1,7² = 2,89 (km/h).

Vậy tốc độ dòng chảy của nước ở đáy sông khi đó là 29 km/h.

b) Thay f = 20,25 km/h vào $\sqrt{f}=\sqrt{v}-1,3,$ ta được:

$\sqrt{20,25}=\sqrt{v}-1,3$

Suy ra $4,5=\sqrt{v}-1,3$ nên $\sqrt{v}=5,8,$ do đó v = 5,8² = 33,64.

Vậy tốc độ dòng chảy của nước ở bề mặt sông khi đó là 33,64 km/h.

Bài 9 trang 53 SBT Toán 9 Tập 1: Cho một hình hộp chữ nhật có các kích thước là 4,8 dm, 3 dm, 15 dm và một hình lập phương có cùng thể tích với hình hộp chữ nhật đó. Tính độ dài cạnh của hình lập phương.

Lời giải:

Thể tích của hình hộp chữ nhật là:

4,8.3.15 = 216 (dm³).

Gọi a (dm) là độ dài cạnh của hình lập phương với a > 0. Khi đó, thể tích của hình lập phương đó là a³ (dm³).

Khi đó, ta có: a³ = 216.

Suy ra $a=\sqrt[3]{216}=6(\text{dm)}.$

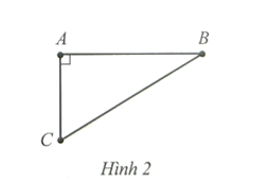
Bài 10 trang 53 SBT Toán 9 Tập 1: Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí A đến trường. Trường của anh An ở vị trí B và trường của em Bình ở vị trí C theo hai hướng vuông góc với nhau (Hình 2). Anh An đi với tốc độ 4 km/h và đến trường sau 15 phút. Em Bình đi với tốc độ 3 km/h và đến trường sau 12 phút. Tính khoảng cách BC giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).

Lời giải:

Đổi 15 phút = $\frac{1}{4}$ giờ; 12 phút = $\frac{1}{5}$ giờ.

Quãng đường anh An đi từ nhà đến trường là: $4\cdot \frac{1}{4}=1\text{\hspace{0.17em}\hspace{0.17em}(km}).$

Quãng đường em Bình đi từ nhà đến trường là: $3\cdot \frac{12}{60}=0,6\text{\hspace{0.17em}\hspace{0.17em}(km})$

Do tam giác ABC vuông tại A nên theo định lí Pythagore, ta có:

BC² = AB² + AC² = 1² + (0,6)² = 1,36.

Do đó $BC=\sqrt{1,36}\approx 1,17\text{\hspace{0.17em}\hspace{0.17em}(km}).$

Vậy khoảng cách BC giữa hai trường xấp xỉ 1,7 km.

Xem thêm Lời giải bài tập Toán 9 sách Cánh diều hay, chi tiết khác:

Bài 2: Một số phép tính về căn bậc hai của số thực

Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài tập cuối chương 3

Bài 1: Tỉ số lượng giác của góc nhọn